தசம எண்களை வகுத்தல்

தசம எண்கள் மீதான செயல்பாடுகள்

தசம எண்களைப் பற்றி நாம் ஏற்கனவே கற்றறிந்தோம். மேலும், தசம எண்களைப் பின்னமாக மாற்றவும், அதன் இடமதிப்பு குறித்தும் நாம் கற்றோம். இங்கு, நாம் தசம எண்கள் மீதான நான்கு அடிப்படைச் செயல்பாடுகள் குறித்துக் கற்போம். 

தசம எண்களை வகுத்தல்

ஒரு சட்டைத் துணிக் கட்டு மொத்தமாக 24.75 மீ உள்ளது. ஒரு கடைக்காரர் அதனை ஒவ்வொன்றும் 1.5 மீ சட்டைத் துணித் துண்டுகளாகப் பிரிக்க விரும்புகிறார் எனில், எத்தனை துண்டுகள் கிடைக்கும்? விடையைக் கண்டறிய 24.75 ஐ 1.5 ஆல் வகுக்க வேண்டும்.

அன்றாட வாழ்வில், நாம் பல்வேறு இடங்களில் இந்தத் தசம எண் வகுத்தலைப் பயன்படுத்துகிறோம்.

(i) மாதிரிகள் மூலம் தசம எண் வகுத்தல் 

• நாம் ஏற்கனவே கற்றறிந்த தசம அட்டவணை முறையில், தசம எண் வகுத்தலில் ஈவு காண முடியும். 

• 2.48 ஐ கட்ட மாதிரி அமைப்பில் கருதுக. 

• 2.48 ÷ 2 ஐக் காண, இரு மாதிரிகளில், இருவேறு வண்ணங்களில் 2.48 ஐக் குறிக்கவும். வகுத்தல் என்பது சமபங்குகளாகப் பிரித்தலே ஆகும். எனவே, நிழலிட்டப் பகுதியைப் படத்திலுள்ளவாறு இரு சமபாகங்களாகப் பிரிக்கவும்.

இங்கு ஒவ்வொரு வண்ணமும் ஈவைக் குறிக்கிறது. அதாவது 1.24 ஆகும். 

எனவே, 2.48 ÷ 2 = 1.24

2.48 ÷ 2 இன் வகுத்தலை வேறு வகையிலும் செய்யலாம்.

பின்வரும் படங்களை உற்று நோக்குக.

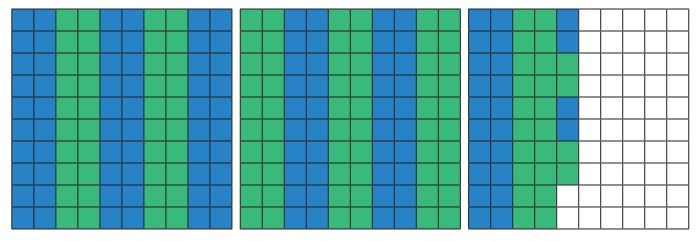
இரண்டு முழுக் கட்ட மாதிரிகளைக் கருதுக. அவற்றை இரு நிரல் கொண்ட சம பாகங்களாகப் பிரித்தால், ஒவ்வொரு குழுவிலும் மொத்தம் 5 பங்குகள் இருக்கும். அது ஒரு முழு மாதிரியைக் குறிக்கும்.

அடுத்து பத்தில் ஒன்றைக் கருதினால், நான்கு பத்தில் ஒன்றுகளை இரு குழுக்களாகப் பிரிக்க, நமக்கு இதேபோல் இரு குழுக்கள் கிடைக்கின்றன. ஒவ்வொரு குழுவும் இரு பத்தில் ஒன்றுகளைக் குறிக்கிறது.

இறுதியாக 8 நூறில் ஒன்றுகளை இரு குழுக்களாகப் பிரிக்க, ஒவ்வொரு குழுவிலும் 4 நூறில் ஒன்றுகள் இருக்கும்.

எனவே, 2.48 ÷ 2 = 1 முழு, 2 பத்தில் ஒன்று, 4 நூறில் ஒன்று = 1.24 

எடுத்துக்காட்டு 1.23 

பரப்பளவு மாதிரிகளைப் பயன்படுத்தி 6.3 ÷3 ஐக் காண்க.

தீர்வு

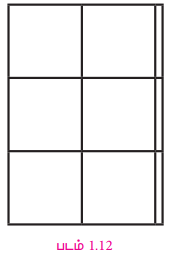
6.3 என்ற தசம எண்ணைக் குறிக்கும் படம் 1.12 காண்க.

6.3 ஐ 3 ஆல் வகுப்பதால், மூன்று வெவ்வேறு வண்ணங்களைப் பயன்படுத்தி, இந்த பரப்பைப் படம் 1.13 இல் உள்ளவாறு மூன்று சம பாகங்களாகப் பிரிக்கலாம்.

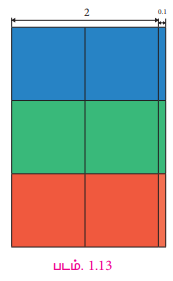
ஒவ்வொரு குழுவும் ஈவு 2.1 ஐக் குறிக்கிறது. 

எனவே, 6.3 ÷ 3 = 2.1

(ii) 10, 100 மற்றும் 1000 ஆல் வகுக்கும் முறை

தசம எண்களை 10, 100 மற்றும் 1000 ஆல் வகுப்பது குறித்துக் கற்போம் 

எடுத்துக்காட்டாக 51.7 ÷ 10 ஐக் கருதுக

51.7= 517/10

எனவே, 51.7 / 10 = 517/10 × 1/10 = 517/100 = 5.17

இதேபோன்று, 51.7 ÷ 100 = 517/10 × 1/100 = 517/1000 = 0.517

இதேபோன்று, 51.7 ÷ 1000= 517/10 × 1/1000 = 517/10000 = 0.0517

பகுதியிலுள்ள பூச்சியங்களின் எண்ணிக்கையும் ஈவாகப் பெறும் தசம இலக்கங்களின் எண்ணிக்கையும் சமம். தசம எண்களை 10, 100 மற்றும் 1000ஆல் வகுக்கும்போது நாம் பின் பற்றும் முறையைப் பற்றிக் காண்போம். பின்வருவனவற்றை உற்றுநோக்கி நிரப்புக.

இவற்றை முயல்க

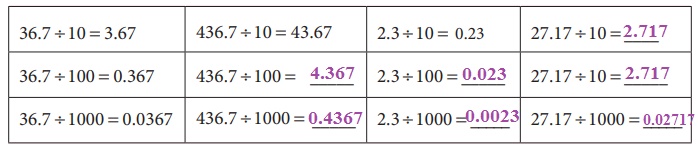
36.7 மற்றும் 3.67 இல் இலக்கங்கள் ஒன்றே , அதாவது 3, 6, 7 ஆகும். ஆனால் தசமப் புள்ளியானது ஈவுப் பகுதியில் இடதுபுறம் ஓர் இடம் நகர்ந்துள்ளது. இங்கு 10 இல் ஒன்றுக்கு அடுத்து ஓரு பூச்சியம் உள்ளது.

இதேபோன்று, 36.7 ÷ 100 = 0.367 இல், தசமப் புள்ளியானது ஈவுப் பகுதியில் இடதுபுறம் இரு இடங்கள் நகர்ந்துள்ளது. 100 இல் 1 இக்கு அடுத்து இரு பூச்சியங்கள் உள்ளன.

இதேபோன்று, 36.7 ÷ 1000 = 0.0367 இல், தசமப் புள்ளியானது ஈவுப் பகுதியில் இடதுபுறம் 3 இடங்கள் நகர்ந்துள்ளது. இங்கு 1000 இல், 1 இக்கு அடுத்து 3 பூச்சியங்கள் உள்ளன.

எனவே 10, 100 மற்றும் 1000 ஆல் வகுக்கும்போது, வகுக்கும் எண் மற்றும் ஈவுப் பகுதியிலுள்ள இலக்கங்கள் மாறாது. ஆனால் ஈவுப் பகுதியிலுள்ள தசமப் புள்ளியானது இடதுபுறம் 1 இக்கு அடுத்துள்ள பூச்சியங்களைப் பொறுத்து நகர்கின்றது.

எனவே,  2.68 ÷ 10=0.268;

2.68 ÷ 100 = 0.0268; 2.68 ÷ 1000= 0.00268.

இவற்றை முயல்க

கீழ்க்கண்டவற்றை வகுக்க

(i) 17.237 ÷ 10

(ii) 17.237÷ 100 

(iii) 17.237 ÷ 1000 

தீர்வு:

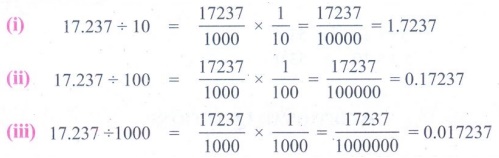
(iii) தசம எண்ணை முழு எண்ணால் வகுத்தல்

தசம எண்களை முழு எண்ணால் வகுக்க, கீழ்க்கண்டவற்றைக் கருதுக. 

குறிப்பு 

ஈவு சரியானதா என்று நாம் கண்டறிய வேண்டும். 9.6 ஐ 10 ஆக முழுமை ஆக்கி 8 ஆல் வகுக்க. 8 ஆனது சிறு மீதியுடன் 10 ஒன்றுகளைப் பிரிப்பதால், 1.2 எனும் ஈவு சரியானது.

இவற்றை முயல்க

கீழ்க்கண்டவற்றின் மதிப்பைக் காண்க.

(i) 46.2 ÷ 3 = ?

(ii) 71.6 ÷ 4 = ?

(iii) 23.24 ÷ 2 = ?

(iv) 127.35 ÷ 9 = ?

(v) 47.201 ÷ 7= ?

தீர்வு : 

மேற்கண்ட மூன்று எடுத்துக்காட்டுகளிலிருந்து தசமப் புள்ளியைக் கருதாமல் எண்களை மட்டும் கொண்டு நம்மால் வகுக்க இயலும் என நாம் அறிகிறோம். மேலும் ஈவின் தசமப்புள்ளியானது வகுபடும் எண்ணின்  தசம இலக்கத்துக்குச் சமமாக இருக்கும்.

எடுத்துக்காட்டாக 52.16 ÷ 4 

5216 ஐ 4 ஆல் வகுக்க

5216/4 =1304 

வகுபடும் எண்ணில் இரண்டு தசம இலக்கங்கள் உள்ளன. எனவே ஈவிலும் இரு தசம இலக்கங்கள் இருக்க வேண்டும்.

எனவே , 52.16 ÷ 4 = 13.04

எடுத்துக்காட்டு 1.24  

1.5 லிட்டர் அளவுள்ள கரும்புச் சாறு ஆனது ஐந்து பேருக்குச் சமமாகப் பங்கிட வேண்டுமெனில் ஒவ்வொருவருக்கும் கிடைக்கும் கரும்புச் சாறின் அளவைக் காண்க...

தீர்வு

கரும்புச் சாறின் அளவு = 1.5 லி

பங்கிடப்பட வேண்டிய நபர்களின் எண்ணிக்கை = 5

ஒவ்வொருவரின் பங்கு = 1.5/5 = 0.3லி

எனவே, ஒவ்வொருவருக்கும் 0.3 லிட்டர் கரும்புச் சாறு கிடைக்கிறது. 

(iv) ஒரு தசம எண்ணை மற்றொரு தசம எண்ணால் வகுத்தல்

கவிதா தனது பிறந்த நாளில் தனது வகுப்பு மாணவிகளுடன் கடலைமிட்டாய் உருண்டைகளைப் பங்கிட விரும்புகிறாள். அவளது சேமிப்பு வங்கியில் ₹ 61.50 உள்ளது. ஒவ்வொரு கடலை மிட்டாய் உருண்டையும் ₹ 1.50 எனில், அவளிடமுள்ள தொகைக்கு எவ்வளவு உருண்டைகளை வாங்க இயலும்? நமது அன்றாட வாழ்வில் இதுபோலப் பல சூழல்களில் ஒரு தசம எண்ணை மற்றொரு தசம எண்ணால் வகுக்க நேரிடுகிறது. 

இதிலிருந்து வகுக்கும் எண்ணும் வகுபடும் எண்ணும் சமத் தசம இலக்கங்கள் பெற்றிருந்தால் வகுத்தலானது இரு இயல் எண்களை வகுப்பது போன்று மிக எளிமையானது. வகுக்கும் எண் மற்றும் வகுபடும் எண்ணின் தசம இலக்கங்கள் வேறாக இருப்பின், முதலில் வகுக்கும் எண்ணைத் தகுந்த 10 இன் அடுக்கால் பெருக்கி முழு எண்ணாக மாற்ற வேண்டும். அதன் பிறகு வகுபடும் எண்ணை 10 இன் அடுக்கால் பெருக்க வேண்டும்.

இவற்றை முயல்க 

கீழ்க்கண்டவற்றை வகுக்கவும். 

(i) 9.25/0.25

(ii) 8.6/4.3

(iii) 44.1/0.21

(iv) 9.6/1.2

தீர்வு :

எடுத்துக்காட்டு 1.25   

ஒரு மகிழுந்து 0.21 மணி நேரத்தில் 16.8 கி.மீ தூரத்தை கடக்கிறது எனில், ஒரு மணி நேரத்தில் அது கடக்கும் தூரம் எவ்வளவு?

தீர்வு

ஒரு மணி நேரத்தில் மகிழுந்து கடந்த தொலைவு = 16.8 / 0.21

வகுக்கும் எண்ணை நூறால் பெருக்கி முழு எண்ணாக மாற்றுக. இதேபோன்று வகுபடும் எண்ணை நூறால் பெருக்குக. 16.8 × 100 / 0.21 × 100 = 1680/21 = 80 கி.மீ.

எடுத்துக்காட்டு 1.26 

ஒரு ஒழுங்கு பலகோணத்தின் சுற்றளவு 17.5 செ.மீ. ஒவ்வொரு பக்கத்தின் அளவு 2.5 செ.மீ எனில், அந்தப் பலகோணத்தில் எத்தனை பக்கங்கள் உள்ளன?

தீர்வு

பல கோணமானது ஒழுங்கு பலகோணம். எனவே அனைத்துப் பக்கங்களும் சமம்.

பலகோணத்திலுள்ள பக்கங்களின் எண்ணிக்கை = சுற்றளவு / ஒரு பக்கத்தின் அளவு 

= 17.5/25 = 175/25 = 7  (வகுக்கும் எண், வகுபடும் எண்ணில் உள்ள தசம இலக்கங்கள் சமம்). 

எனவே, பலகோணமானது ஏழு பக்கங்களைக் கொண்டது. எனவே, பலகோணத்தின் பக்கங்களின் எண்ணிக்கை 7 ஆகும்.

சிந்திக்க

30 மாத்திரைகள் கொண்ட ஒரு மாத்திரை அட்டையின் விலை ₹ 62.63 எனில், ஒரு மாத்திரையின் விலையைக் காண்க.

தீர்வு