வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் - இரண்டு தளங்களுக்கு இடைப்பட்ட கோணம் (Angle between two planes) | 12th Maths : UNIT 6 : Applications of Vector Algebra
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்
இரண்டு தளங்களுக்கு இடைப்பட்ட கோணம் (Angle between two planes)
10. இரண்டு தளங்களுக்கு இடைப்பட்ட கோணம் (Angle between two planes)
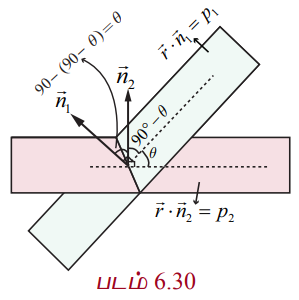
இரு தளங்களுக்கு இடைப்பட்ட கோணமானது அத்தளங்களின் செங்கோடுகளுக்கு இடைப்பட்ட கோணத்திற்குச் சமமாகும்.
தேற்றம் 6.18
நிரூபணம்
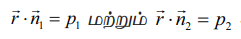ஆகிய இரு தளங்களுக்கு இடைப்பட்ட குறுங்கோணம் θ என்பது அத்தளங்களின் செங்குத்து வெக்டர்கள் 
மற்றும் 
ஆகியவற்றுக்கு இடைப்பட்ட கோணமாகும். எனவே,
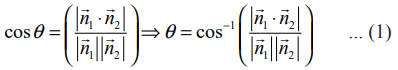
குறிப்புரை
தேற்றம் 6.19
a1x + b1y + c1z + d1 = 0 மற்றும் a2x + b2y + c2z + d2 = 0 ஆகிய தளங்களுக்கு இடைப்பட்ட குறுங்கோணம் θ எனில், θ = cos−1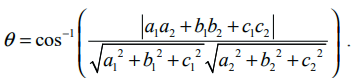 
நிரூபணம்
a1x + b1y + c1z + d1 = 0 மற்றும் a2x + b2y + c2z + d2 =0 ஆகிய தளங்களின் செங்கோட்டு வெக்டர்கள் முறையே மற்றும் , என்க. பின்னர்,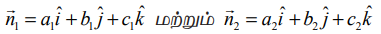 
ஆகும்.
எனவே தேற்றம் 6.18−ன் சமன்பாடு (1)−ஐப் பயன்படுத்தி, தளங்களுக்கு இடைப்பட்ட குறுங்கோணம் θ எனில்,
எனப்பெறுகிறோம்
குறிப்புரை
(i) a1x + b1y + c1z + d1 = 0 மற்றும் a2x + b2y + c2z + d2 =0 என்ற தளங்கள் ஒன்றுக்கொன்று செங்குத்து எனில், a1a2 + b1b2 + c1c2 = 0 ஆகும்.
(ii) a1x + b1y + c1z + d1 = 0 மற்றும் a2x + b2y + c2z + d2 =0 என்ற தளங்கள் இணையானவை எனில்,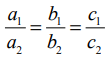 
ஆகும்.
(iii) ax + by + cz = p என்ற தளத்திற்கு இணையான தளத்தின் சமன்பாடு ax + by + cz = k, k ∈ ℝ ஆகும்.
எடுத்துக்காட்டு 6.47
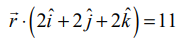மற்றும் 4x−2y+2z=15 ஆகிய தளங்களுக்கு இடைப்பட்ட குறுங்கோணத்தைக் காண்க.
தீர்வு
