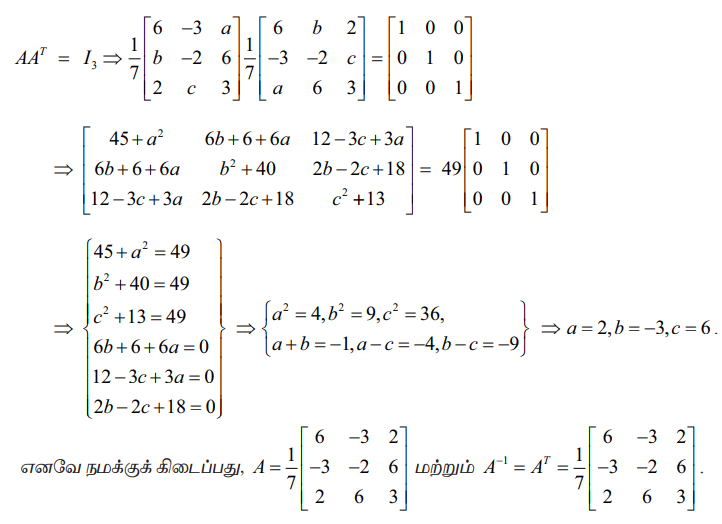வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் | பூச்சியமற்ற கோவை அணியின் நேர்மாறு (Inverse of a Non−Singular square matrix) - வடிவக் கணிதத்தில் அணிகளின் பயன்பாடுகள் (Application of matrices to Geometry) | 12th Maths : UNIT 1 : Applications of Matrices and Determinants

12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 1 : அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள்

வடிவக் கணிதத்தில் அணிகளின் பயன்பாடுகள் (Application of matrices to Geometry)

வடிவக் கணிதத்தில், அணிகளின் பயன்பாடுகளில் ஒரு சிறப்பு வகையான பூச்சியமற்றக் கோவை அணிகள் பரவலாக பயன்படுத்தப்படுகிறது. எளிமையைக் கருத்தில் கொண்டு, நாம் இரு பரிமாண பகுமுறை வடிவக் கணிதத்தை மட்டும் இங்கு கருதுவோம்.

4. வடிவக் கணிதத்தில் அணிகளின் பயன்பாடுகள்

(Application of matrices to Geometry)

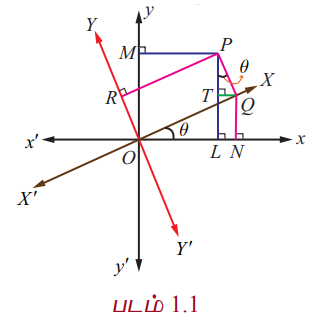
ஆதியை O எனவும் x'Ox மற்றும் y'Oy என்பவற்றை முறையே x − அச்சாகவும் y − அச்சாகவும் கொள்வோம். ஆய தளத்தில் P என்பது (x,y) ஆயத்தொலைவுகளாகக் கொண்ட புள்ளி என்க. x − அச்சையும் y − அச்சையும் ஆதியைப் பொருத்து θ கோணத்திற்கு படத்தில் உள்ளவாறு சுழற்றப்படுகிறது என்க. X’OX மற்றும் Y’OY என்பன முறையே புதிய X − அச்சு மற்றும் Y − அச்சு என்க. (X, Y) என்பது புதிய அச்சில் P−ன் ஆயத்தொலைவுகள் என்க. படம் 1.1−லிருந்து நாம் பெறுவது,

x = OL = ON − LN = X cos θ − QT = X cos θ − Y sin θ,

y = PL = PT + TL = QN + PT = X sin θ + Y cos θ.

இச்சமன்பாடுகள் ஓர் ஆய அச்சுத் தொலைவு முறையினை மற்றொரு ஆய அச்சுத் தொலைவு முறையாக மாற்ற வழி வகுக்கின்றன. மேற்காணும் இரு சமன்பாடுகளை பின்வரும் அணி வடிவமைப்பில் எழுதலாம்.

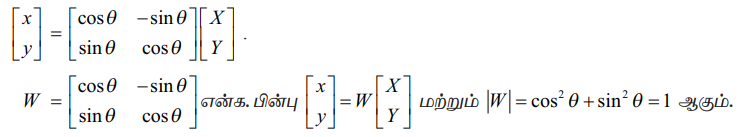
எனவே, W −க்கு நேர்மாறு அணி உள்ளது மற்றும் W −1 = 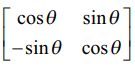. இங்கு W−1 =WT

என்றிருப்பதைக் கவனிக்கவும். நேரெதிர் உருமாற்றத்தினைப் பின்வருமாறு பெறலாம்.

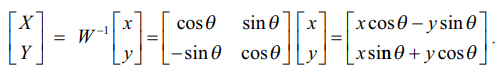
இவ்வாறாக X = x cos θ − y sin θ, Y = x sin θ + y cos θ

என்ற உருமாற்றத்தினைப் பெறுகிறோம். இந்த உருமாற்றம் கணினி வரைபட நுட்பத்தில் பயன்படுத்தப்படுகிறது. இப்பயன்பாட்டினை W = 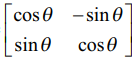என்ற அணி நிர்ணயிக்கின்றது.

அணி W ஆனது W −1 =WT அதாவது WWT =WTW = I என்ற சிறப்புப் பண்பினைப் பெற்றுள்ளதை அறிக.

வரையறை 1.3

ஒரு சதுர அணி A −க்கு AAT = ATA = I எனில், A ஆனது செங்குத்து அணி எனப்படும்.

குறிப்பு

ஒரு அணி A என்பது செங்குத்து அணியாக இருப்பதற்குத் தேவையான மற்றும் போதுமான நிபந்தனையாதெனில் A பூச்சியமற்ற கோவை அணியாகவும் மற்றும் A−1 = AT எனவும் இருக்க வேண்டும்.

எடுத்துக்காட்டு 1.11

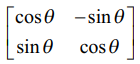என்பது செங்குத்து அணி என நிறுவுக.

தீர்வு

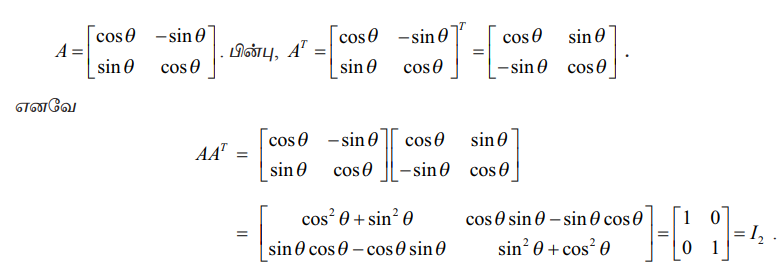
இதேபோல் ATA = I2. எனவே AAT = ATA = I2 ⇒ A ஆனது செங்குத்து அணியாகும்.

எடுத்துக்காட்டு 1.12

A = 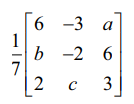என்பது செங்குத்து அணி எனில் a, b மற்றும் c களின் மதிப்பைக் காண்க. இதிலிருந்து A−1 −ஐக் காண்க.

தீர்வு

A என்பது செங்குத்து அணி. எனவே, AAT = ATA = I3 . எனவே நாம் பெறுவது

Tags : Definition, Theorem, Formulas, Solved Example Problems | Inverse of a Non-Singular Square Matrix வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் | பூச்சியமற்ற கோவை அணியின் நேர்மாறு (Inverse of a Non−Singular square matrix).

12th Maths : UNIT 1 : Applications of Matrices and Determinants : Application of matrices to Geometry Definition, Theorem, Formulas, Solved Example Problems | Inverse of a Non-Singular Square Matrix in Tamil : 12th Standard TN Tamil Medium School Samacheer Book Back Questions and answers, Important Question with Answer. 12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 1 : அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் : வடிவக் கணிதத்தில் அணிகளின் பயன்பாடுகள் (Application of matrices to Geometry) - வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் | பூச்சியமற்ற கோவை அணியின் நேர்மாறு (Inverse of a Non−Singular square matrix) : 12 ஆம் வகுப்பு தமிழ்நாடு பள்ளி சமசீர் புத்தகம் கேள்விகள் மற்றும் பதில்கள்.