நேரியச் சமன்பாட்டுத் தொகுப்பின் தீர்வுகள் (Solution to a System of Linear equations)

3. நேரியச் சமன்பாட்டுத் தொகுப்பின் தீர்வுகள்

(Solution to a System of Linear equations)

நேரியச் சமன்பாட்டுத் தொகுப்பின் தீர்வின் இயல்பை பின்வரும் நிலைகளின் மூலம் அறிந்து கொள்ளலாம்:

நிலை (i)

பின்வரும் நேரியச் சமன்பாட்டுத் தொகுப்பைக் கருத்தில் கொள்வோம்.

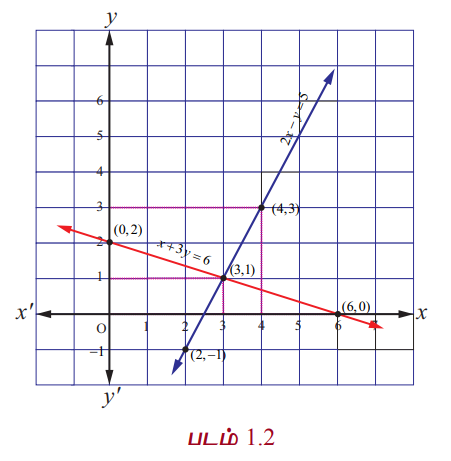
2x − y = 5,     ... (1)

x + 3y = 6.     ... (2)

இந்த இரு சமன்பாடுகள் இருபரிமான பகுமுறை வடிவியலில் இரட்டைக் கோடுகளைக் குறிக்கின்றன. (படம் 1.2 −ஐ பார்க்க). (1) −லிருந்து நாம் பெறுவது

x = (5+y) / 2     ... (3)

(3) −ஐ (2) −ல் பிரதியிட்டுச் சுருக்கக் கிடைப்பது y = 1.

y = 1 என (1) −ல் பிரதியிட்டுச் சுருக்கக் கிடைப்பது x = 3.

x = 3 மற்றும் y = 1 சமன்பாடுகள் (1) மற்றும் (2) நிறைவு செய்கின்றன.

அதாவது (1)−ன் தீர்வானது (2)−க்கும் தீர்வாகிறது.

எனவே இத்தொகுப்பை ஒருங்கமைவு உடையது மற்றும் தொகுப்பிற்கு ஒரே ஒரு தீர்வு (3, 1) எனக் கூறுகிறோம்..

புள்ளி (3, 1) என்பது கோடுகள் 2x − y = 5 மற்றும் x + 3y = 6 வெட்டிக் கொள்ளும் புள்ளியாகும்.

நிலை (ii)

பின்வரும் நேரியச் சமன்பாட்டுத் தொகுப்பை கருத்தில் கொள்வோம்.

3x + 2y = 5,     ...(1) 

6x + 4y = 10    ...(2)

சமன்பாடு (1)−லிருந்து கிடைப்பது

x =  (5 − 2y) / 3      ... (3)

(3)−ஐ (2)−ல் பிரதியிட்டுச் சுருக்கினால் நாம் பெறுவது 0 = 0 .

இதிலிருந்து நாம் அறிவது சமன்பாடு (2) ஆனது சமன்பாடு (1) −ன் தொடக்கநிலை உருமாற்றமாகும். சமன்பாடு (2)−ஐ 2−ஆல் வகுக்கக் கிடைப்பது சமன்பாடு (1) ஆகும். எனவே ஒரே ஒரு சமன்பாடு (1)−ஐ வைத்துக்கொண்டு x மற்றும் y −க்கு ஒரே ஒரு தீர்வு காண இயலாது.

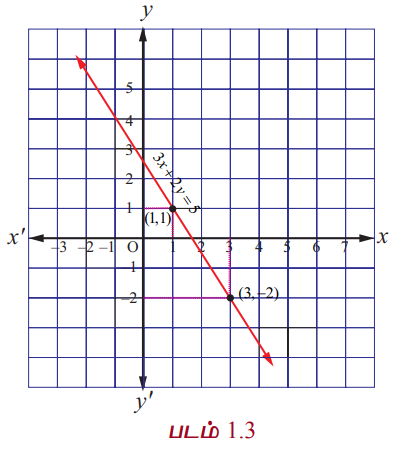
எனவே y = t என்ற மதிப்பை நாம் எடுத்துக்கொள்ள வேண்டிய நிர்ப்பந்தத்திற்கு உள்ளாகிறோம். பின்பு x = (5−2t) / 3. இங்கு t என்பது ஒரு மெய் எண். சமன்பாடுகள் (1) மற்றும் (2) ஒரே ஒரு கோட்டை (ஒன்றின் மீது ஒன்று அமையும் கோடுகள்) இரு பரிமான பகுமுறை வடிவியலில் குறிக்கின்றன.. (படம் 1.3−ஐ பார்க்க). எனவே தொகுப்பானது ஒருங்கமைவு உடையது மற்றும் (1)−ன் தீர்வுகள் (2)−க்கு தீர்வுகளாகும். மற்றும் t எந்த ஒரு மெய்யெண் மதிப்பைப் பெறுவதால் தொகுப்பிற்கு எண்ணற்ற தீர்வுகள் உண்டு.

நிலை (iii)

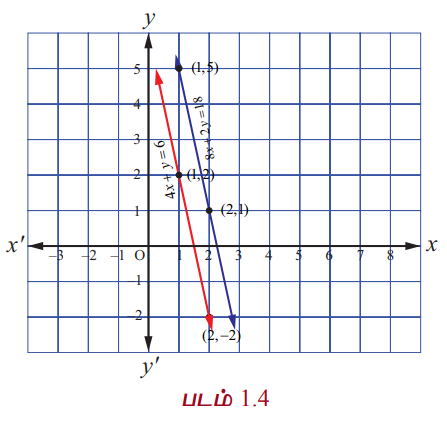
பின்வரும் நேரியச் சமன்பாட்டுத் தொகுப்பை கருத்தில் கொள்வோம்.

4x + y = 6,  ...(1) 

8x + 2y = 18.  ...(2)

சமன்பாடு (1)−லிருந்து நாம் பெறுவது

x = (6 − y) / 4 ...(3)

(3) −ஐ (2) −ல் பிரதியிட்டுச் சுருக்கக் கிடைப்பது 12 = 18.

இது ஒரு முரண்பாடான முடிவு ஆகும். இதிலிருந்து நாம் அறிவது யாதெனில் சமன்பாடு (2) ஆனது சமன்பாடு (1) உடன் ஒருங்கமைவற்றது. எனவே (1) −ன் தீர்வுகள் (2) −க்கு தீர்வாகாது.

எனவே தொகுப்பானது ஒருங்கமைவு அற்றது. மற்றும் தொகுப்பிற்கு தீர்வு கிடையாது. இச்சமன்பாடுகள் இருபரிமான பகுமுறை வடிவியலில் இரு இணை நேர்க்கோடுகளை (ஒன்றின் மீது ஒன்று அமையாத) குறிக்கின்றன. (பார்க்க படம் 1.4). ஒன்றின் மீது ஒன்று அமையாத இரு இணைக்கோடுகள் எப்பொழுதும் மெய் புள்ளியில் சந்திப்பது இல்லை என நாம் அறிவோம். 

குறிப்பு

(1) தொகுப்பில் உள்ள ஏதேனும் இரு சமன்பாடுகளை இடம் மாற்றினால் தொகுப்பிற்கான தீர்வுகளில் மாற்றம் ஏற்படாது.

(2) ஒரு பூச்சியமற்ற மாறிலியால் தொகுப்பில் உள்ள ஒரு சமன்பாட்டைப் பெருக்கி மாற்றி அமைத்தால் தொகுப்பிற்கான தீர்வுகளில் மாற்றம் ஏற்படாது.

(3) நேரியச் சமன்பாடுகளின் தொகுப்பின் எந்தவொரு சமன்பாட்டினை, அச்சமன்பாட்டுடனும், அத்தொகுப்பின் பிறிதொரு சமன்பாட்டின் பூச்சியமில்லா எண்ணின் பெருக்கற்பலனைக் கூட்டிப் பிரதியிடல் அத்தொகுப்பின் தீர்வினை மாற்றாது.

வரையறை1.8

ஒரு நேரியச் சமன்பாட்டுத் தொகுப்பானது குறைந்தது ஒரு தீர்வு பெற்றிருந்தால், தொகுப்பானது ஒருங்கமைவுடையது எனப்படும். ஒரு தீர்வு கூட பெறவில்லையெனில் தொகுப்பானது ஒருங்கமைவற்றது எனப்படும்.

குறிப்புரை

நேரியச் சமன்பாட்டுத் தொகுப்பில் உள்ள சமன்பாடுகளின் எண்ணிக்கைக்கு மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கைக்குச் சமம் எனில் கெழுக்களின் அணி A ஆனது சதுர அணியாக இருக்கும். மேலும் A ஆனது பூச்சியமற்ற கோவை அணியாகவுமிருப்பின் நேரியச் சமன்பாட்டுத் தொகுப்பிற்குப் பின்வரும் முறைகளில் ஏதேனும் ஒரு முறையில் தீர்வு காணலாம். (i) நேர்மாறு அணி காணல் முறை, (ii) கிராமரின் விதி, (iii) காஸ்ஸியன் நீக்கல் முறை