கிராமரின் விதி (Cramer’s Rule)

3. (ii) கிராமரின் விதி (Cramer’s Rule)

நேரியல் சமன்பாட்டுத் தொகுப்பில் உள்ள கெழுக்கள் அணியானது சதுர அணியாகவும் பூச்சியமற்ற அணிக்கோவை அணியாகவம் இருந்தால் மட்டுமே இம்முறையை பயன்படுத்த இயலும். இம்முறையை பின்வரும் சமன்பாட்டுத் தொகுப்பின் மூலம் விவரிப்போம்.

a11 x1 + a12 x2 + a13 x3 = b1,

a21 x1 + a22 x2 + a23 x3 = b2,

a31 x1 + a32 x2 + a33 x3 = b3,

இங்கு கெழுக்கள் அணியானது, 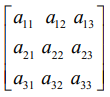  பூச்சியமற்ற கோவை அணி. எனவே 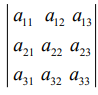≠ 0.

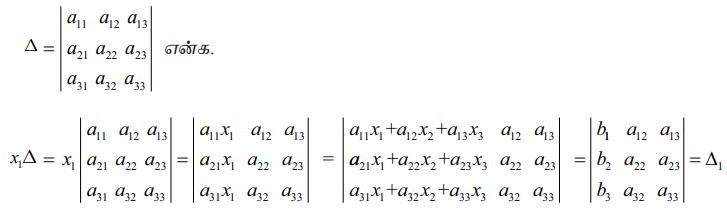
Δ ≠ 0 ஆதலால், நாம் பெறுவது x1 = Δ1 / Δ.

இதேபோல், நாம் பெறுவது

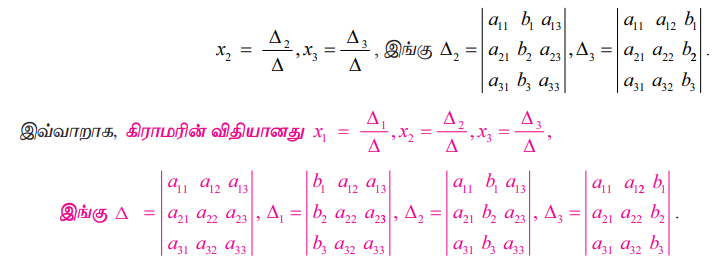
குறிப்பு

Δ −ல் உள்ள முதல் நிரலில் உள்ள உறுப்புகளான a11, a21, a31 களுக்குப் பதில் முறையே b1, b2, b3 களைப் பிரதியிடக் கிடைப்பது Δ1.

Δ−ல் உள்ள இரண்டாவது நிரலில் உள்ள உறுப்புகளான a12, a22, a32 களுக்குப் பதில் முறையே b1, b2, b3 களைப் பிரதியிடக் கிடைப்பது Δ2 ஆகும்.

Δ−ல் உள்ள மூன்றாவது நிரலில் உள்ள உறுப்புகளான a13, a23, a33 களுக்குப் பதில் முறையே b1, b2, b3 களைப் பிரதியிடக் கிடைப்பது Δ3 ஆகும்.

Δ = 0 எனில் கிராமரின் விதியை பயன்படுத்த இயலாது.

எடுத்துக்காட்டு 1.25

x1 − x2 = 3, 2x1 + 3x2 + 4x3 = 17, x2 + 2x3 = 7 என்ற நேரியச் சமன்பாடுகளின் தொகுப்பைத் தீர்க்கவும்.

தீர்வு

பின்வரும் அணிக்கோவைகளின் மதிப்பை முதலில் காண்போம்.

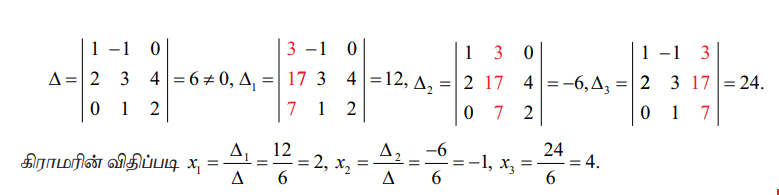
எனவே தீர்வானது (x1 = 2, x2 = −1, x3 = 4).

எடுத்துக்காட்டு 1.26

T20 ஆட்டமொன்றில் கடைசி ஓவரில் 1 பந்து மட்டும் வீசப்பட வேண்டிய நிலையில் ஓர் அணியானது 6 ரன்கள் (ஓட்டங்கள்) பெற்றால் மட்டுமே வெற்றி பெறும் நிலையில் இருந்தது. கடைசி பந்து மட்டையருக்கு வீசப்பட்டது. அவர் அதனை மிக உயரம் செல்லுமாறு அடிக்கிறார். பந்தானது செங்குத்து தளத்தில் சென்ற பாதை அத்தளத்தில் y = ax2 + bx + c என்ற சமன்பாட்டின்படி உள்ளது. பந்தானது (10,8), (20,16), (40,22) என்ற புள்ளிகள் வழியாகச் செல்கிறது எனில் அவ்வணியானது ஆட்டத்தை வென்றதா என்பதை முடிவு செய்யலாமா? உனது விடையினை கிராமர் விதியைக் கொண்டு நியாயப்படுத்துக. (எல்லா தொலைவுகளும் மீட்டர் அளவில் உள்ளன. பந்து சென்ற பாதையின் தளமானது மிகத்தொலைவில் உள்ள எல்லைக் கோட்டினை (70,0) என்ற புள்ளியில் சந்திக்கும்)

தீர்வு

y = ax2 + bx + c என்ற பாதையானது (10,8), (20,16), (40,22) என்ற புள்ளிகள் வழிச் செல்கிறது. ஆதலால் 100a + 10b + c = 8,400a + 20b + c = 16,1600a + 40b + c = 22 என்ற சமன்பாடுகள் கிடைக்கின்றன. கிராமரின் விதியை பயன்படுத்த பின்வருவனவற்றைக் காண்போம்.

x = 70 எனில் y = 6 எனக் கிடைக்கிறது. எனவே பந்தானது எல்லைக்கோட்டிற்கு நேர் மேலாக 6 மீ உயரத்தில் செல்கிறது மற்றும் எல்லைக் கோட்டின் அருகில் உள்ள ஆட்டக்காரர் எகிறிக் குதித்துப் பிடிக்க முயன்றாலும் அவரால் அப்பந்தினைப் பிடிக்க இயலாது. எனவே அப்பந்து மிகப்பெரிய 6 ஆகச் சென்றது மற்றும் அவ்வணி ஆட்டத்தினை வென்றது.