வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் - ஓர் அணியின் தரம் (Rank of a matrix) | 12th Maths : UNIT 1 : Applications of Matrices and Determinants
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 1 : அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள்
ஓர் அணியின் தரம் (Rank of a matrix)
3. ஓர் அணியின் தரம் (Rank of a matrix)
ஓர் அணியின் அணித்தரத்தை வரையறுக்க உபஅணி மற்றும் சிற்றணிக்கோவை பற்றி தெரிந்திருத்தல் அவசியமாகும்.
A என்பது ஏதேனும் ஓர் அணி என்க. இதிலிருந்து சில நிரைகளையும், நிரல்களையும் நீக்குவதால் கிடைக்கும் அணி A−இன் ஓர் உபஅணியாகும். ஓர் அணியே தனக்குத்தானே உபஅணியாகும். ஏனெனில் அவ்வணியிலிருந்து பூச்சிய எண்ணிக்கை நிரைகளையும் மற்றும் பூச்சிய எண்ணிக்கை நிரல்களையும் நீக்குவதால் கிடைக்கப் பெறுவதாகும். ஒரு சதுர உபஅணியின் அணிக்கோவை மதிப்பு சிற்றணிக்கோவையாகும்.
வரையறை 1.6
ஓர் அணி A −இன் தரம் என்பது அதன் பூச்சியமற்ற சிற்றணிக்கோவைகளின் உச்ச வரிசையாகும். A−இன் தரத்தை ρ(A) எனக்குறிப்பிடுவர். ஒரு பூச்சிய அணியின் தரம் ஆனது பூச்சியம் என வரையறுக்கப்படும்.
குறிப்பு
(i) ஓர் அணியில் குறைந்தது ஒரு பூச்சியமற்ற உறுப்பு இருப்பின் ρ(A) ≥ 1.
(ii) அலகு அணி In –ன் தரம் n ஆகும்.
(iii) A என்ற அணியின் தரம் r எனில் A −ல் குறைந்தபட்சம் ஒரு r வரிசையுடைய பூச்சியமற்ற சிற்றணிக்கோவையாவது இடம்பெற்றிருத்தல் வேண்டும் மற்றும் A−ன் ஒவ்வொரு r + 1 வரிசை மற்றும் அதைவிட அதிகமான வரிசை கொண்ட சிற்றணிக் கோவைகளின் மதிப்புகள் பூச்சியங்களாகியிருத்தல் வேண்டும்.
(iv) A −ன் வரிசை m × n எனில் ρ(A) ≤ min {m,n} = m, n களில் குறைந்த எண்.
(v) n வரிசையுடைய ஒரு சதுர அணிக்கு நேர்மாறு காணத் தேவையான மற்றும் போதுமான நிபந்தனை ρ (A) = n.
எடுத்துக்காட்டு 1.15
பின்வரும் அணிகளுக்கு அணித்தரம் காண்க : 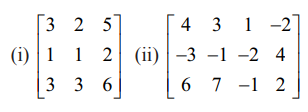
தீர்வு
(i) A = 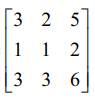 என்க. A ஆனது 3 × 3 வரிசையுடைய அணி. எனவே ρ(A) ≤ min {3,3} = 3.
என்க. A ஆனது 3 × 3 வரிசையுடைய அணி. எனவே ρ(A) ≤ min {3,3} = 3.
உச்ச சிற்றணிக்கோவையின் வரிசை 3.
A −விற்கு ஒரே ஒரு 3 வரிசையுடைய சிற்றணிக்கோவைதான் உண்டு. அதன் மதிப்பு
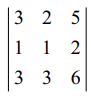 = 3 (6 − 6) − 2 (6 − 6) + 5 (3 − 3) = 0 . எனவே, ρ(A) < 3.
= 3 (6 − 6) − 2 (6 − 6) + 5 (3 − 3) = 0 . எனவே, ρ(A) < 3.
அடுத்து 2 வரிசையுடைய சிற்றணிக்கோவை தேர்வு செய்வோம். அதில் ஒரு 2 வரிசையுடைய சிற்றணிக்கோவை 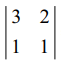 = 3 − 2 = 1 ≠ 0. எனவே p(A) = 2.
= 3 − 2 = 1 ≠ 0. எனவே p(A) = 2.
(ii) 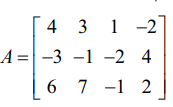 என்க. A ஆனது 3 × 4 வரிசையுடைய அணி.
என்க. A ஆனது 3 × 4 வரிசையுடைய அணி.
எனவே ρ(A) ≤ min {3, 4} = 3.
உச்ச சிற்றணிக்கோவையின் வரிசை 3. அவை
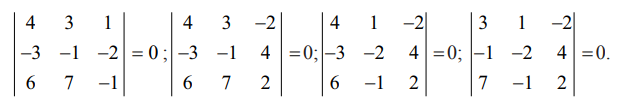
எனவே, ρ(A) < 3 அடுத்து 2−ஆம் வரிசையின் பூச்சியமற்ற சிற்றணிக்கோவை ஏதேனும் ஒன்று A உள்ளதா எனப்பார்ப்போம். இது சாத்தியமாகும்,
ஏனெனில் 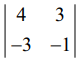 = −4 + 9 = 5 ≠ 0.
= −4 + 9 = 5 ≠ 0.
எனவே, ρ(A) = 2.
குறிப்புரை
ஓர் அணியின் வரிசை அதிகமாக இருக்கும் பட்சத்தில், பூச்சியமற்ற சிற்றணிக்கோவைகளின் உச்ச வரிசை தேடி அணியின் தரம் காண்பது எளிதல்ல. அணித்தரம் காண்பதற்கு வேறு ஒரு எளிமையான முறை உள்ளது. இம்முறையில் அணியின் வரிசை அதிகமாக இருந்தாலும் அணித்தரம் காண்பது எளியது. இம்முறையானது ஒரு அணியின் நிரை−ஏறுபடி வடிவத்திற்கு சமமான அணியின் அணித்தரம் காண்பதாகும். ஓர் அணியானது நிரை−ஏறுபடி வடிவில் இருப்பின் அதன் முதன்மை மூலைவிட்ட உறுப்புகளுக்கு கீழ் உள்ள அனைத்து உறுப்புகளும் பூச்சியங்களாகும். (இது a11, a12,... என்ற நிலைகளில் உள்ள மூலைவிட்ட உறுப்புக்களை சேர்க்கும் கோடாகும்).
எனவே ஒரு சிற்றணிக்கோவையின் மதிப்பு பூச்சியம் அல்லது பூச்சியம் இல்லை எனக் காண்பது எளியது. இதன் மூலம் அணித்தரம் காண்பது எளியது.
எடுத்துக்காட்டு 1.16
பின்வரும் ஏறுபடி வடிவத்திலுள்ள அணிகளுக்கு அணித்தரம் காண்க :
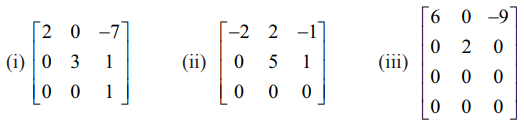
தீர்வு
A = 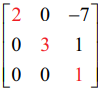 என்க. A −ஆனது 3 × 3 வரிசையுடைய அணி மற்றும் ρ(A) ≤ 3
என்க. A −ஆனது 3 × 3 வரிசையுடைய அணி மற்றும் ρ(A) ≤ 3
மூன்றாம் வரிசையுடைய சிற்றணிக்கோவை |A| = 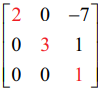 = (2) (3) (1) = 6 ≠ 0.
= (2) (3) (1) = 6 ≠ 0.
எனவே, ρ(A) = 3.
எனவே இங்கு மூன்று அபூச்சிய நிரைகள் உள்ளன என்பதைக் கூர்ந்து நோக்குக.
(ii) A = 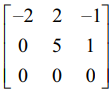 என்க. A ஆனது 3 × 3 வரிசையுடைய அணி எனவே ρ (A) ≤ 3.
என்க. A ஆனது 3 × 3 வரிசையுடைய அணி எனவே ρ (A) ≤ 3.
மூன்றாம் வரிசையுடைய சிற்றணிக்கோவை |A| =  = (−2) (5) (0) = 0
= (−2) (5) (0) = 0
எனவே ρ(A) ≤ 2.
பல இரண்டாம் வரிசையுடைய சிற்றணிக்கோவைகள் உள்ளன. அவற்றுள் ஒன்று
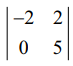 = (−2) (5) = −10 ≠ 0. எனவே, ρ(A) = 2.
= (−2) (5) = −10 ≠ 0. எனவே, ρ(A) = 2.
இங்கு இரண்டு அபூச்சிய நிரைகள் உள்ளன என்பதை நோக்குக. மூன்றாவது நிரை பூச்சிய நிரையாகும்.
(iii) A = 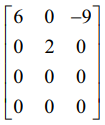 என்க. A ஆனது 4 × 3 வரிசையுடைய அணியாகும் மற்றும் ρ(A) < 3.
என்க. A ஆனது 4 × 3 வரிசையுடைய அணியாகும் மற்றும் ρ(A) < 3.
அனைத்து மூன்றாம் வரிசையுடைய சிற்றணிக் கோவைகளின் மதிப்பு 0 ஆகும். எனவே ρ(A) < 3.
கடைசி இரு நிரைகள் பூச்சிய நிரைகளாகும். நிறைய இரண்டாம் வரிசையுடைய சிற்றணிக்கோவைகள் உள்ளன. அவற்றுள் ஒன்று 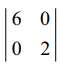 = (6) (2) = 12 ≠ 0. எனவே, ρ(A) = 2.
= (6) (2) = 12 ≠ 0. எனவே, ρ(A) = 2.
இரண்டு அபூச்சிய நிரைகள் உள்ளன என்பதை நோக்குக. மூன்றாவது மற்றும் நான்காவது நிரைகள் பூச்சிய நிரைகளாகும்.
மேல் உள்ள எடுத்துக்காட்டுகளிலிருந்து, ஏறுபடி வடிவிலுள்ள ஓர் அணியின் அணித்தரமானது அபூச்சிய நிரைகளின் எண்ணிக்கைக்குச் சமம் எனக்காண்கிறோம். இதனைப் பின்வரும் தேற்றமாக நிரூபணமில்லாமல் கூறுவோம்.
தேற்றம் 1.11
நிரை ஏறுபடி வடிவிலுள்ள ஓர் அணியின் அணித்தரம் அபூச்சிய நிரைகளின் எண்ணிக்கையாகும்.
இதனைப் பின்வரும் தேற்றமாக நிரூபணமில்லாமல் கூறுவோம்.
தேற்றம் 1.12
அபூச்சிய அணியின் தரமானது அதன் ஏறுபடி வடிவத்தில் உள்ள அபூச்சிய நிரைகளின் எண்ணிக்கைக்குச் சமம்.
எடுத்துக்காட்டு 1.17
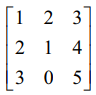 என்ற அணியை ஏறுபடி வடிவத்திற்கு மாற்றி அணித்தரம் காண்க.
என்ற அணியை ஏறுபடி வடிவத்திற்கு மாற்றி அணித்தரம் காண்க.
தீர்வு
A =  என்க. தொடக்க நிலை நிரை செயலிகள் பயன்படுத்தக் கிடைப்பது
என்க. தொடக்க நிலை நிரை செயலிகள் பயன்படுத்தக் கிடைப்பது
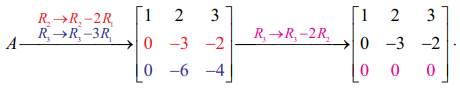
கடைசி சமான அணி ஏறுபடி வடிவத்தில் உள்ளது மற்றும் இரண்டு அபூச்சிய நிரைகளைப் பெற்றுள்ளது. எனவே ρ(A) = 2.
எடுத்துக்காட்டு 1.18
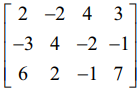 என்ற அணியை ஏறுபடி வடிவில் மாற்றி அணித்தரம் காண்க.
என்ற அணியை ஏறுபடி வடிவில் மாற்றி அணித்தரம் காண்க.
தீர்வு
கொடுத்துள்ள அணியை A என்க. தொடக்க நிலை நிரைச் செயலிகளைப் பயன்படுத்தக் கிடைப்பது
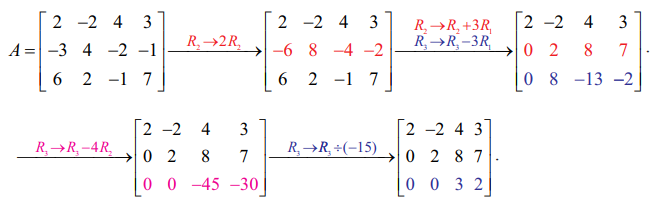
கடைசி சமான அணியானது நிரை−ஏறுபடி வடிவில் உள்ளது மற்றும் மூன்று அபூச்சிய நிரைகளை உடையது. எனவே, ρ(A) = 3.
தொடக்க நிலை நிரைச் செயலிகள் ஓர் அணியின் மீது செயல்படுத்துவது என்பது அந்த அணியை முன்புறமாக ஒரு சிறப்பு வகை (special class) அணிகளால் பெருக்குவதாகும். அந்த அணிகள் தொடக்க நிலை அணிகள் (Elementary matrices) எனப்படும்.
வரையறை 1.7
ஓர் அலகு அணியில் ஒரே ஒரு தொடக்க நிலை உருமாற்றத்தினால் கிடைக்கும் அணியை தொடக்க நிலை அணி என வரையறுக்கப்படுகிறது.
குறிப்புரை
மூன்று வரிசையுடைய அணிகளுக்கான தொடக்க நிலை அணிகள் எல்லாம் 3 வரிசையுடைய சதுர அணிகளாகும். அவ்வணிகள் ஓர் அலகு அணி I3−இல் ஒரே ஒரு தொடக்க நிலை நிரை செயலிகளை செயல்படுத்துவதால் கிடைப்பதாகும். கொடுத்துள்ள அணி A−இல் செயல்படுத்தப்படும் ஒவ்வொரு தொடக்க நிலை நிரை செயலிகளும் A−இன் முன்புறமாக தொடக்க நிலை அணியால் பெருக்கக் கிடைப்பதாகும். இதேபோல் A−இல் செயல்படுத்தப்படும் ஒவ்வொரு தொடக்க நிலை நிரல் செயலிகளும் A−இன் பின்புறமாக தொடக்க நிலை அணியால் பெருக்கக் கிடைப்பதாகும். இந்த அத்தியாயத்தில் தொடக்க நிலை நிரைச் செயலிகள் மட்டுமே நாம் பயன்படுத்துவோம்.
எடுத்துக்காட்டாக A = 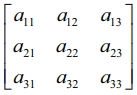 ஐக் கருதுக
ஐக் கருதுக
A −ன் மீது R2 → R2 + λR3 என்ற நிரை உருமாற்றத்தினைச் செயல்படுத்துவோம் என்க. இங்கு λ ≠ 0 என்பது ஒரு மாறிலி. பின்பு கிடைப்பது,
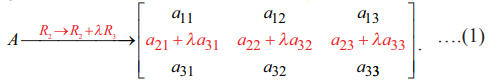 ….(1)
….(1)
இம்மாற்றத்தினைப் பின்வருமாறு தொடக்கநிலை அணியினைக் கொண்டும் பெறலாம்.

எனவே, A −ன் மீது R2 → R2 + λR3 என்ற தொடக்கநிலை உருமாற்றத்தால் ஏற்படும் விளைவானது A −ஐ 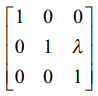 என்ற தொடக்க நிலை அணியால் முன்புறமாகப் பெருக்குவதால் கிடைக்கும் அணியாகும்.
என்ற தொடக்க நிலை அணியால் முன்புறமாகப் பெருக்குவதால் கிடைக்கும் அணியாகும்.
இவ்வாறே, பின்வருவனவற்றைக் காட்ட முடியும்:
(i) R2 ↔ R3 என்ற தொடக்க நிலை உருமாற்றம் செயற்படுத்துவதால் ஏற்படும் விளைவானது A −ஐ 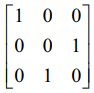 என்ற தொடக்கநிலை அணியால் முன்புறமாகப் பெருக்குவதால் கிடைக்கும் அணியாகும்.
என்ற தொடக்கநிலை அணியால் முன்புறமாகப் பெருக்குவதால் கிடைக்கும் அணியாகும்.
(ii) A−ன் மீது R2 ↔ λR2 என்ற தொடக்க நிலை உருமாற்றத்தால் ஏற்படும் விளைவானது A− ஐ 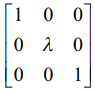 என்ற தொடக்க நிலை அணியால் முன்புறமாகப் பெருக்குதால் கிடைக்கும் அணியாகும்.
என்ற தொடக்க நிலை அணியால் முன்புறமாகப் பெருக்குதால் கிடைக்கும் அணியாகும்.
நிரூபணமின்றி பின்வரும் முடிவைக் கூறுவோம்:
தேற்றம் 1.13
ஒரு வரிசைக்கிரமமான தொடக்கநிலைச் செயலிகளைக் கொண்டு ஒவ்வொரு பூச்சியமற்ற கோவை அணியினை ஓர் அலகு அணியாக உருமாற்றம் செய்யலாம்.
மேற்காணும் தேற்றத்தினை விளக்க A = 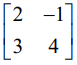 என்ற அணியினைக் கருதுக.
என்ற அணியினைக் கருதுக.
இங்கு |A| = 12 + 3 = 15 ≠ 0. எனவே A ஆனது பூச்சியமற்ற அணிக்கோவை அணியாகும். A –ஐ I2 −ஆக ஒரு வரிசைக்கிரமமான தொடக்கநிலை நிரை செயலிகளால் மாற்றுவோம்.
முதற்படியாக. A −ன் a11ஐ 1 என மாற்றுவதற்கான நிரை மாற்றிகளைத் தேடுவோம்.
இதற்குத் தேவையான தொடக்கநிலை உருமாற்றம் R1 → (1/2) R1, ஆகும்.
இதற்கொத்த தொடக்கநிலை அணி E1 = 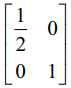 ஆகும்.
ஆகும்.
பின்பு, நமக்குக் கிடைப்பது, E1 A = 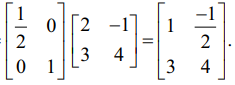
அடுத்தாக E1A என்ற அணியின் a11 –ற்குக் கீழுள்ள அனைத்து உறுப்புகளைப் பூச்சியமாக்குவோம். இந்த விளக்க எடுத்துக்காட்டில் a21 என்ற உறுப்பு மட்டுமே உள்ளது. இதற்குத் தேவையான தொடக்க நிலை உருமாற்றம் R2 → R2 + (−3)R1 ஆகும்.
இதற்கொத்த தொடக்க நிலை அணி E2 = 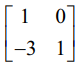 ஆகும்.
ஆகும்.
பின்பு, நமக்குக் கிடைப்பது E2 (E1 A) = 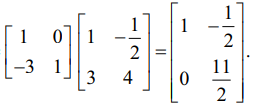
அடுத்தாக, E2 (E1 A) − இல் உள்ள a22 −ஐ 1−ஆக மாற்ற வேண்டும். இதற்குத் தேவையான தொடக்க நிலை உருமாற்றம் R2 → (2/11)R2 ஆகும்.
இதற்கொத்த தொடக்க நிலை அணியானது E3 = 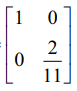 ஆகும்.
ஆகும்.
பின்பு நமக்குக் கிடைப்பது E3 (E2 (E1A)) = 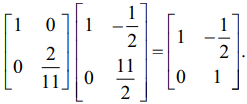
முடிவாக, E3 (E2 (E1A)) −ன் a12 −ஐ பூச்சியமாக்குவோம். இதற்குத் தேவையான தொடக்கநிலை நிரை மாற்றம் R1 → R1 + (1/2) R2 ஆகும். இதற்கொத்த தொடக்கநிலை அணி E4 =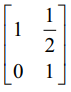 ஆகும்.
ஆகும்.
பின்பு, நமக்குக் கிடைப்பது, E4 (E3 (E2 (E1A))) = 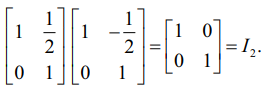
மேல் உள்ள தொடர்ச்சியாக உள்ள தொடக்க நிலை உருமாற்றங்களை பின்வருமாறு எழுதுவோம்.

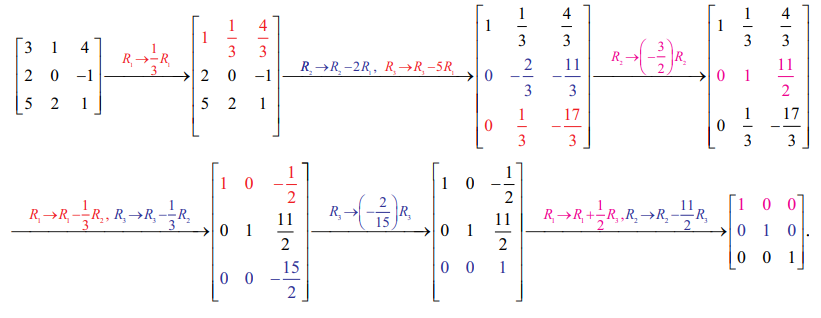
எடுத்துக்காட்டு 1.19
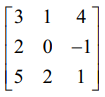 என்பது பூச்சியமற்ற அணிக்கோவை அணி எனக்காட்டுக மற்றும் இவ்வணியை தொடக்க நிலை உருமாற்றங்கள் மூலம் அலகு அணியாக மாற்றுக.
என்பது பூச்சியமற்ற அணிக்கோவை அணி எனக்காட்டுக மற்றும் இவ்வணியை தொடக்க நிலை உருமாற்றங்கள் மூலம் அலகு அணியாக மாற்றுக.
தீர்வு
A = 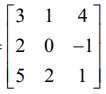 என்க. |A| = 3 (0 + 2) – 1 (2 + 5) + 4 (4 − 0) = 6 – 7 + 16 = 15 ≠ 0. எனவே, A ஆனது பூச்சியமற்ற அணிக்கோவை அணியாகும்.
என்க. |A| = 3 (0 + 2) – 1 (2 + 5) + 4 (4 − 0) = 6 – 7 + 16 = 15 ≠ 0. எனவே, A ஆனது பூச்சியமற்ற அணிக்கோவை அணியாகும்.