வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் | பூச்சியமற்ற கோவை அணியின் நேர்மாறு (Inverse of a Non−Singular square matrix) - நேர்மாறு அணிகளின் பண்புகள் (Properties of inverse of matrices) | 12th Maths : UNIT 1 : Applications of Matrices and Determinants
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 1 : அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள்
நேர்மாறு அணிகளின் பண்புகள் (Properties of inverse of matrices)
3. நேர்மாறு அணிகளின் பண்புகள் (Properties of inverse of matrices)
நேர்மாறு காணத்தக்க அணிகளின் பண்புகள் சிலவற்றையும் அதில் ஒரு சில பண்புகளையும் நிரூபிக்க உள்ளோம்.
தேற்றம் 1.4
A என்பது பூச்சியமற்றக் கோவை அணி எனில்
(i) |A−1| = 1 / |A|
(ii) (AT)−1 = (A−1)T
(iii) (λ A)−1 = (1 / λ) A−1, இங்கு λ என்பது பூச்சியமற்ற திசையிலி
நிரூபணம்
A என்பது பூச்சியமற்றக் கோவை அணி என்க. எனவே |A| ≠ 0 மற்றும் A−1 காண இயலும். வரையறைப்படி,
AA−1 = A−1A = In … (1)
(i) சமன்பாடு (1) மூலம் கிடைப்பது |AA−1| = |A−1A│= |In|.
அணிக்கோவையின் பெருக்கல் விதியைப் பயன்படுத்த |A| |A−1| = |In| = 1.
எனவே, |A−1| = 1 / |A|
(ii) சமன்பாடு (1) − இலிருந்து, (AA−1)T = (A−1A)T = (In)T.
நிரை நிரல் அணியின் வரிசைமாற்று விதிப்படி, (A−1)T AT = AT (A−1)T = In
எனவே, (AT)−1 =(A−1)T.
(iii) λ என்பது பூச்சியமற்ற திசையிலி ஆதலால் சமன்பாடு (1) − இலிருந்து,
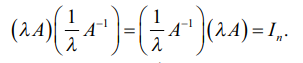
எனவே, (λA)−1 = (1 / λ) A−1
தேற்றம் 1.5 (இடது நீக்கல் விதி)
A, B மற்றும் C என்பன n வரிசையுடைய சதுர அணிகள் என்க. A என்பது பூச்சியமற்றக் கோவை அணி மற்றும் AB = AC எனில், B = C.
நிரூபணம்
A ஆனது பூச்சியமற்றக் கோவை அணி. எனவே A−1 காண இயலும் மற்றும் AA−1 = A−1A = In. AB = AC −இன் இருபுறமும் முன்புறமாக A−1 −ஆல் பெருக்கக் கிடைப்பது A−1(AB) = A−1(AC). அணிப்பெருக்கலின் சேர்ப்பு மற்றும் அணியின் நேர்மாறு பண்பைப் பயன்படுத்த நமக்குக் கிடைப்பது B = C.
தேற்றம் 1.6 (வலது நீக்கல் விதி)
A, B மற்றும் C என்பன n வரிசையுடைய சதுர அணிகள் என்க. A என்பது பூச்சியமற்றக் கோவை அணி மற்றும் BA = CA எனில், B = C.
நிரூபணம்
A ஆனது பூச்சியமற்ற கோவை அணி. எனவே A−1 காண இயலும் மற்றும் AA−1 = A−1A = In. BA = CA −யின் இருபுறமும் பின்புறமாக A−1 −ஆல் பெருக்கக் கிடைப்பது (BA)A−1 = (CA)A−1. அணிப்பெருக்கலின் சேர்ப்பு மற்றும் அணியின் நேர்மாறு பண்பைப் பயன்படுத்த நமக்குக் கிடைப்பது B = C.
குறிப்பு
A ஆனது பூச்சியக்கோவை அணி மற்றும் AB = AC அல்லது BA = CA, எனில் B − யும் C − யும் சமமாக இருக்க வேண்டியது இல்லை. எடுத்துக்காட்டாக,
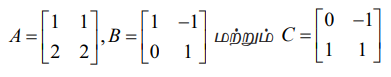 எனக்கொள்க.
எனக்கொள்க.
இங்கு |A| = 0 மற்றும் AB = AC ஆனால் B ≠ C என்பது குறிப்பிடத்தக்கது.
தேற்றம் 1.7 (நேர்மாறுகளின் வரிசை மாற்று விதி)
A மற்றும் B என்பன ஒரே வரிசையுடைய பூச்சியமற்ற கோவை அணிகள் எனில் அவற்றின் பெருக்கற்பலன் AB −யும் பூச்சியமற்ற கோவை அணியாகும் மற்றும் (AB)−1 = B−1A−1.
நிரூபணம்
A மற்றும் B என்பன n வரிசையுடைய பூச்சியமற்ற கோவை அணிகள் என்க. எனவே |A| ≠ 0, |B| ≠ 0, எனவே A−1 மற்றும் B−1 காணமுடியும் மற்றும் அவைகள் n வரிசையுடையனவாக இருக்கும். மேலும் AB மற்றும் B−1A−1 −களின் பெருக்கற்பலன்கள் n வரிசையுடையனவாக இருக்கும். அணிக்கோவைகளின் பெருக்கற்பலன் விதிப்படி கிடைப்பது |AB| = |A| |B| ≠ 0. எனவே AB −யும் பூச்சியமற்ற கோவை அணியாகும் மற்றும்
(AB) (B−1A−1) = (A(BB−1)) A−1 = (AIn) A−1 = AA−1 = In ;
(B−1A−1) (AB) = (B−1(A−1A))B = (B−1 In)B = B−1B = In.
எனவே (AB)−1 = B−1A−1
தேற்றம் 1.8 (இரட்டிப்பு நேர்மாறு விதி)
A என்பது பூச்சியமற்றக் கோவை அணி எனில் A−1−யும் பூச்சியமற்ற கோவை அணி மற்றும் (A−1) −1 = A.
நிரூபணம்
A என்பது பூச்சியமற்றக் கோவை அணி என்க. எனவே |A| ≠ 0 மற்றும் A−1 காண இயலும்.
|A−1| = 1 / |A| ≠ 0 ⇒ A−1 ஆனது பூச்சியமற்ற கோவை அணியாகும் மற்றும்
AA−1 = A−1A = I.
AA−1 = 1 ⇒ (AA−1)−1 = I ⇒ (A−1) −1 A −1 = I. … (1)
(1)−ன் இருபுறமும் A −ஆல் பின்புறமாக பெருக்கக் கிடைப்பது (A−1)−1 = A.
தேற்றம் 1.9
A என்பது n வரிசையுடைய பூச்சியமற்றக் கோவை அணி எனில்
(i) (adj A)−1 = adj (A−1) = (1 / |A|) A
(ii) |adj A│ = |A|n−1
(iii) adj (adj A) = |A|n−2 A
(iv) adj (λA) = λ n−1 adj (A) λ என்பது பூச்சியமற்ற திசையிலி
(v) |adj (adj A)| = |A|(n−1)2
(vi) (adj A)T = adj (AT)
நிரூபணம்
A என்பது பூச்சியமற்றக் கோவை அணி ஆதலால் |A| ≠ 0. எனவே
(i) A−1 = (1 / | A|) (adj A) ⇒ adj A = | A| A−1 ⇒ (adj A)−1 = (|A |) A−1)−1 = (1 / |A |) (A−1)-1 = (1 / |A |) A.
A −விற்கு பதில் A−1 –ஐ adj A = | A| A−1 −ல் பிரதியிட adj (A)−1 = | A−1| (A−1)−1 = (1 / |A |) A.
எனவே கிடைப்பது (adj A)−1 = adj (A−1) = (1/|A |) A.
(ii) A(adj A) = (adj A)A = |A|In ⇒ det (A(adj A)) = det ((adj A) A) = det (|A| In)
⇒ |A| |adj A| = |A|n ⇒ |adj A| = |A| n−1
(iii) B என்பது n வரிசையுடைய பூச்சியமற்றக் கோவை அணி எனில்
B (adj B) = (adj B) B = |B| In.
B = adj A எனப்பிரதியிடக் கிடைப்பது, (adj A) (adj (adj A)) = |adj A| In.
|adj A| = |A|n−1 ஆதலால், (adj A) (adj (adj A)) = |A|n−1 In.
இருபுறமும் A ஆல் முன்புறமாக பெருக்கக் கிடைப்பது
A ((adj A) (adj (adj A))) = A (|A|n−1 In).
அணிப்பெருக்கலின் சேர்ப்பு விதியைப் பயன்படுத்தக் கிடைப்பது,
(A (adj A)) (adj (adj A)) = A (|A| n−1 In).
எனவே (|A| In) (adj (adj A)) = |A| n−1 A. அதாவது adj (adj A) = |A|n−2 A.
(iv) A −விற்கு λA என adj (A) = |A|A−1 என்பதில் பிரதியிடக் கிடைப்பது
adj(λA) = |λA| (λ.A)−1 = λn |A│ (1/λ) A−1 = λn−1 |A| A−1 = λn−1 adj(A) .
(v) (iii) −ன்படி adj (adj A) = |A|n−2 A. இருபுறமும் அணிக்கோவை காணக் கிடைப்பது
|adj (adj A)| = | | A| n−2 A | = (|A| n−2)n |A| = |A| n2−2+1 = |A|( n−1)2
(vi) A −விற்கு பதில் AT என A−1 = (1 / |A|) adj A என்பதில் பிரதியிடக் கிடைப்பது,
(AT)−1 = (1 / |AT|) adj (AT) எனவே
adj (AT) = |AT| (AT)−1 = |A| (A−1)T = ( |A| A−1) T = (|A| (1 / |A|) adj A)T = (adj A)T.
குறிப்பு
A என்பது 3 வரிசையுடைய பூச்சியமற்றக் கோவை அணி எனில் |A| ≠ 0. தேற்றம் 1.9 (ii) படி கிடைப்பது |adj A| = |A|2 மற்றும் |adj A| ஆனது மிகை. எனவே | A| = ± √ [ |adj A| ].
எனவே 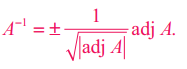
மேலும் தேற்றம் 1.9 (iii) இன் படி கிடைப்பது, A = (1 / |A|) adj (adj A).
எனவே, A ஆனது 3 படி வரிசையுடைய பூச்சியமற்றக் கோவை எனில், 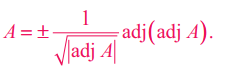
எடுத்துக்காட்டு 1.4
A என்பது ஒற்றை வரிசையுடைய பூச்சியமற்றக் கோவை அணி எனில் |adj A| என்பது மிகை என நிறுவுக.
தீர்வு
A என்பது 2m + 1 வரிசையுடைய பூச்சியமற்றக் கோவை அணி என்க. இங்கு m = 0, 1, 2, . . . எனவே |A| ≠ 0 மற்றும் தேற்றம் 1.9 (ii) இன் படி கிடைப்பது, |adj A| = |A|(2m+1)−1 = |A|2m.
|A|2m என்பது எப்பொழுதும் மிகை, எனவே |adj A| ஆனது மிகை.
எடுத்துக்காட்டு 1.5
adj (A) = 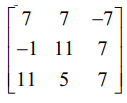 எனில், A −ஐக் காண்க.
எனில், A −ஐக் காண்க.
தீர்வு
|adj (A)| = 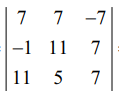 = 7 (77 − 35) – 7 (−7 − 77) − 7 (−5 − 121) = 1764 > 0.
= 7 (77 − 35) – 7 (−7 − 77) − 7 (−5 − 121) = 1764 > 0.
எனவே
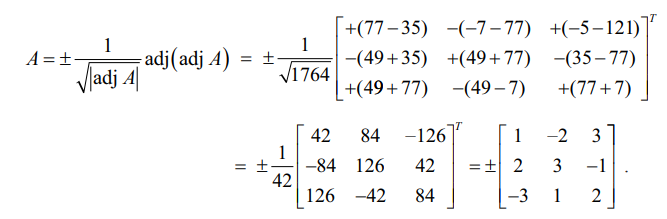
எடுத்துக்காட்டு 1.6
adj A = 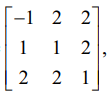 எனில் A−1 −ஐக் காண்க.
எனில் A−1 −ஐக் காண்க.
தீர்வு
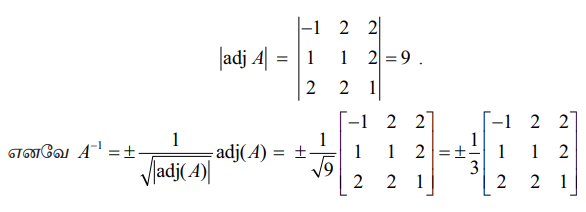
எடுத்துக்காட்டு 1.7
A என்பது சமச்சீர் அணி எனில் adj A சமச்சீர் அணி என நிறுவுக.
தீர்வு
A என்பது சமச்சீர் அணி என்க. எனவே AT = A மற்றும் தேற்றம் 1.9 (vi) இன் படி கிடைப்பது adj (AT) = (adj A)T ⇒ adj A = (adj A)T ⇒ adj A ஆனது சமச்சீராகும்.
தேற்றம் 1.10
A மற்றும் B என்பன n வரிசையுடைய பூச்சியமற்ற கோவை அணிகள் எனில்
adj (AB) = (adj B) (adj A).
நிரூபணம்
A−விற்கு பதில் AB என adj (A) = |A| A−1 −ல் பிரதியிட
adj (AB) = |AB| (AB)−1 = (|B| B−1) (|A| A−1) = adj(B) adj(A).
எடுத்துக்காட்டு 1.8
A = 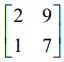 எனில் (AT)−1 = (A−1)T என்ற பண்பை சரிபார்க்க.
எனில் (AT)−1 = (A−1)T என்ற பண்பை சரிபார்க்க.
தீர்வு
| A| = (2) (7) − (9) (1) = 14 − 9 = 5. எனவே, A−1 = 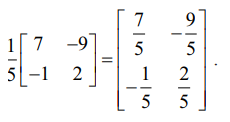
எனவே,
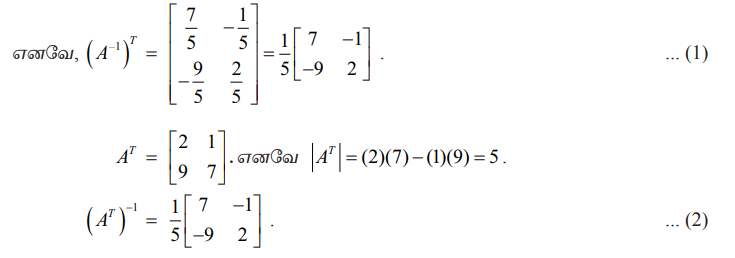
(1) மற்றும் (2)−லிருந்து கிடைப்பது, (A−1)T = (AT)−1. எனவே கொடுத்துள்ள பண்பு சரிபார்க்கப்பட்டது.
எடுத்துக்காட்டு 1.9
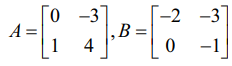 எனக்கொண்டு (AB)−1 = B−1A−1 என்பதைச் சரிபார்க்க.
எனக்கொண்டு (AB)−1 = B−1A−1 என்பதைச் சரிபார்க்க.
தீர்வு
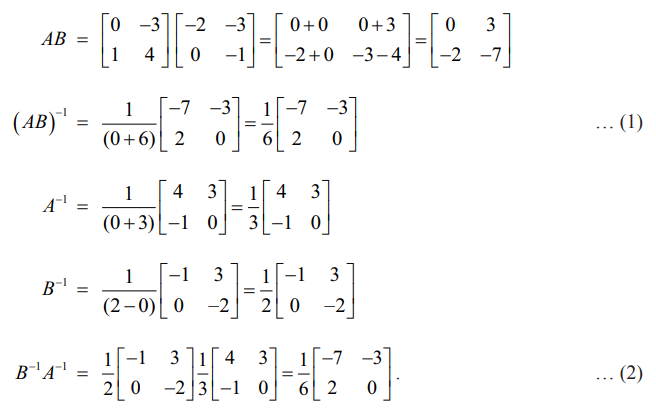
அணிகள் (1) மற்றும் (2) சமம். எனவே (AB)−1 = B−1A−1 என்பது சரிபார்க்கப்பட்டது.
எடுத்துக்காட்டு 1.10
A = 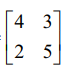 எனில், A2 + xA + yI2 =O2 எனுமாறு x மற்றும் y −ஐ காண்க. இதிலிருந்து A−1 காண்க.
எனில், A2 + xA + yI2 =O2 எனுமாறு x மற்றும் y −ஐ காண்க. இதிலிருந்து A−1 காண்க.
தீர்வு
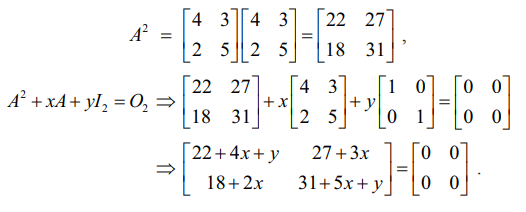
இதிலிருந்து நமக்குக் கிடைப்பவை 22 + 4x + y = 0, 31 + 5x + y = 0, 27 + 3x = 0 மற்றும் 18 + 2x = 0
எனவே x = −9 மற்றும் y = 14. பின்பு நமக்குக் கிடைப்பது A2 − 9A + 14I2 = O2.
இச்சமன்பாட்டின் இருபுறமும் A−1 −ஆல் பெருக்கக் கிடைப்பது A − 9I2 + 14A−1 = O2.
இதிலிருந்து கிடைப்பது