கூட்டுச் சராசரி (அ) (சராசரி)

கூட்டுச் சராசரி (அ) (சராசரி)

இப்போது, மையப்போக்கு அளவீடுகளில் ஒன்றான கூட்டுச் சராசரியைக் காண்போம். இந்தச் சூழ்நிலையைக் கவனியுங்கள்

மணியும் இரவியும் கடற்கரையில் ஓர் ஒப்பந்தத்தின் அடிப்படையில் இருவரும் சமமாகப் பகிர்ந்து கொள்ள கிளிஞ்சல்களைச் சேகரிக்கத் தொடங்கினர். அந்த ஒப்பந்தமானது, சேகரிக்கப்பட்ட கிளிஞ்சல்களை இருவரும் சமமாகப் பிரித்துக்கொள்வது என்பதாகும். இறுதியாக, மணி 50 கிளிஞ்சல்களையும் இரவி 30 கிளிஞ்சல்களையும் மட்டுமே சேகரித்தனர். இப்போது இருவரும் கிளிஞ்சல்களைச் சமமாகப் பகிர்ந்துகொண்டால், ஒவ்வொருவரும் பெறும் கிளிஞ்சல்களின் எண்ணிக்கையைக் கண்டுபிடிக்கவும்? 

நாம் கூட்டுச் சராசரி அல்லது சராசரியைப்பயன்படுத்தி இதைக் காண்போம். சராசரியைக் கண்டுபிடிக்க இரண்டு எண்களையும் கூட்டி 2 ஆல் வகுக்கவும்.

எனவே, சராசரி = 50+30/2 = 80/2 = 40

சராசரியானது 30 இக்கும் மற்றும் 50 இக்கும் இடையே அமைந்துள்ளது.

எனவே ஒவ்வொருவரும் பெறும் கிளிஞ்சல்களின் எண்ணிக்கை 40 ஆகும்.

இவ்வாறு சராசரியைக் கண்டுபிடிக்க விவரங்களைக் கூட்டி அவற்றின் எண்ணிக்கையால் வகுக்க வேண்டும்.

சராசரி = விவரங்களின் கூடுதல் (மதிப்புகள்) / விவரங்களின் எண்ணிக்கை 

முயன்று பார்

பின்வரும் தரவுகளைக் கொண்டு கூட்டுச் சராசரி அல்லது சராசரியைக் காண்க.

(i) ஒரு வாரத்தில் கதிர் படிப்பதற்காக எடுத்துக்கொண்ட நேரம், 3 மணி, 4மணி 5மணி, 3 மணி, 4மணி, 3.45 மணி, மற்றும் 4.15 மணி.

தீர்வு :

சராசரி = விவரங்களின் கூடுதல் (மதிப்புகள்) / விவரங்களின் எண்ணிக்கை

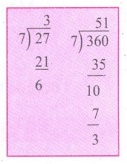
= [ 3 + 4 + 5 + 3 + 4 + 3.45 + 4.15 ] / 7

= 27 / 7 = 3 மணி  52 நி

சராசரி = 3 : 52 மணி

(ii) ஐந்து பாடங்களில் முகில் பெற்ற மதிப்பெண்கள் 75, 91, 48, 63, 51.

தீர்வு :

சராசரி = விவரங்களின் கூடுதல் (மதிப்புகள்) / விவரங்களின் எண்ணிக்கை

= [ 75 + 91+ 48 + 63 + 51 ] / 5 = 328 / 5

சராசரி = 65.6

(iii) காய்கறிகளுக்காக ஐந்து நாட்களுக்குச் செலவழித்த பணம் ₹ 120, ₹ 80, ₹ 75, ₹ 95 மற்றும் ₹ 86 ஆகும்.

தீர்வு :

சராசரி = விவரங்களின் கூடுதல் (மதிப்புகள்) / விவரங்களின் எண்ணிக்கை

= [120 + 80 + 75 + 95 + 86] / 5 = 456 / 5

 சராசரி = 91.2

எடுத்துக்காட்டு 5.1  

ஒரு தொழிலாளியின் தினசரி ஊதியம், 10 நாள்களுக்குப் பின்வருமாறு தரப்பட்டுள்ளது எனில், அவரது சராசரி வருமானத்தைக் கண்டுபிடி.

தீர்வு

சராசரி = விவரங்களின் கூடுதல் (மதிப்புகள்) / விவரங்களின் எண்ணிக்கை

= [250+350+100+400+150+270+450+320+610+750] / 10

= 3650/10 = 365

எனவே, அவருடைய சராசரி வருமானம் ₹ 365 ஆகும்.

எடுத்துக்காட்டு 5.2 

9 விவரங்களின் சராசரி 24 எனில், அவ்விவரங்களின் கூட்டுத்தொகையைக் காண்க. 

தீர்வு

சராசரி = மதிப்புகளின் கூடுதல்/மதிப்புகளின் எண்ணிக்கை

எனவே, 24 = மதிப்புகளின் கூடுதல்/9

மதிப்புகளின் கூடுதல் =9×24 = 216.

எடுத்துக்காட்டு 5.3 

ஒரு பள்ளியிலுள்ள 15 ஆசிரியர்களின் சராசரி வயது 42 ஆகும். அந்த ஆசிரியர்களின் வயதானது 35, 42, 48, X, X + 8, 40, 43, 50, 46, 50, 37, 32, 38, 41 மற்றும் 40 (ஆண்டுகளில்) ஆகும் எனில், X இன் மதிப்பைக் கண்டுபிடித்து, ஆசிரியர்களின் வயதுகளையும் காண்க. 

தீர்வு

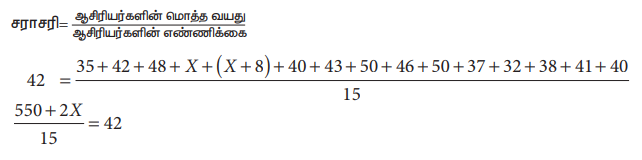
சாரசரி = ஆசிரியர்களின் மொத்த வயது/ஆசிரியர்களின் எண்ணிக்கை

42 = 35+42 +48 + X+ (X +8) +40 +43 +50+46 +50 +37+32 + 38 +41+40 / 15

550 + 2X/15 = 42

550 + 2X = 42×15

= 630 

2X = 630 – 550 

2X = 80

X = 80/2

X = 40

ஆகவே, (X) என்ற ஆசிரியரின் வயது 40 மற்றும் (X + 8) என்ற ஆசிரியரின் வயது 48 ஆகும் (40 + 8).

எடுத்துக்காட்டு 5.4 

பின்வரும் எண்களின் சராசரி 38 என்றால், x இன் மதிப்பைக் கண்டறியவும்? 

48, x, 37, 38, 36, 27, 35, 34, 38, 49, 33. 

தீர்வு

சராசரி = எண்களின் கூடுதல்/எண்களின் எண்ணிக்கை

38 = [48 + x + 37 + 38 + 36 + 27 + 35 + 34 + 38 + 49 + 33] /11

38 =[ 375 + x]/11

38×11= 375 + x

 418 = 375+x

 x = 418-375

 x = 43

எனவே, x இன் மதிப்பு 43 ஆகும்.

சிந்திக்க

கீழேக் கொடுக்கப்பட்டுள்ள எடுத்துக்காட்டுக்குச் சராசரியின் பண்புகளைச் சரிபார்க்கவும்.

(i) சராசரியுடன் 2 ஐக் கூட்டினால், தனிப்பட்ட மதிப்புகளில் என்ன நிகழும். 

தீர்வு :

கொடுக்கப்பட்ட எண்கள்  3, 6, 9, 12, 15

சராசரி = எண்களின் கூடுதல்/எண்களின் எண்ணிக்கை

= [3 + 6 + 9 + 12 + 15] / 5 = 45 / 5 = 9

 2 ஆல் அதிகரித்தால் ,

9 + 2 = எண்களின் கூடுதல் / 5

எண்களின் கூடுதல் = 5 × 11 = 55

வேறுபாடு  = 55 – 45 = 10

∴ சராசரி 2 ஆல்  அதிகரித்தால் ஒவ்வொரு எண்ணும் 2 ஆல் அதிகரிக்கப்படும்.

(ii) முதல் இரண்டு மதிப்புகளில் 3 ஐக் கூட்டியும் கடைசி இரண்டு மதிப்புகளில் 3 ஐக் குறைத்தால், புதிய சராசரி என்னவாக இருக்கும்?

தீர்வு :

முதல் இரண்டு மதிப்புகளில் 3 ஐக் கூட்டினால் கிடைக்கும் எண்களின் சராசரி

3 + 3, 6 + 3 => 6, 9.

இரண்டு மதிப்புகளில் 3 ஐக் குறைத்தால் கிடைக்கும் எண்களின் சராசரி

12 – 3, 15 – 3 => 9, 12.

∴ புதிய எண்களின் சராசரி  = [ 6 + 9 + 9+ 9+ 12 ] / 5

 = 45 / 9 = 9

சராசரியில் எந்த மாற்றமும் இல்லை.

சில ஆச்சரியமான சராசரிகள் இங்கே! 

1. சராசரியாக, ஒருவர் நிமிடத்திற்கு 17 முறை கண் சிமிட்டுகிறார். அதாவது வருடத்திற்கு 5.2 மில்லியன் முறை. 

2. ஒரு மனிதன் ஆண்டுக்குச் சராசரியாகச் சுமார் 1460 கனவுகள் காண்கிறான். அதாவது, ஓர் இரவுக்குச் சுமார் 4 கனவுகள். 

3. ஒரு G2 நட்சத்திரத்தின் சராசரி வாழ்க்கையின் அடிப்படையில் சூரியனின் தற்போதைய வயது 4.5 பில்லியன் ஆண்டுகள் என மதிப்பிடப்பட்டுள்ளது.