Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я»Ї | Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ««Я»Ї Я«фЯ«░Я»ЂЯ«хЯ««Я»Ї Я«ЁЯ«▓Я«ЋЯ»Ђ 5 | 7Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ - Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ (Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ) | 7th Maths : Term 3 Unit 5 : Statistics
7Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ««Я»Ї Я«фЯ«░Я»ЂЯ«хЯ««Я»Ї Я«ЁЯ«▓Я«ЋЯ»Ђ 5 : Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я»Ї
Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ (Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ)
Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ (Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ)
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«фЯ«┐Я«░Я«цЯ«┐Я«еЯ«┐Я«цЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«х Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕЯ«»Я»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ«ЪЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«џЯ»ѓЯ«┤Я»ЇЯ«еЯ«┐Я«▓Я»ѕЯ«ЋЯ«│Я»ѕ Я«еЯ«ЙЯ««Я»Ї Я«хЯ«┐Я«хЯ«ЙЯ«цЯ«┐Я«цЯ»ЇЯ«цЯ»ІЯ««Я»Ї. Я«ЄЯ«хЯ»ѕЯ«цЯ«хЯ«┐Я«░ Я«хЯ»ЄЯ«▒Я»єЯ«еЯ»ЇЯ«ц Я««Я«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ«фЯ»Ї Я«фЯ«┐Я«░Я«цЯ«┐Я«еЯ«┐Я«цЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«х Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«│Я«хЯ»ѕЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«»Я»ЂЯ««Я»Ї Я«џЯ«┐Я«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї? Я«ЄЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«џЯ»ѓЯ«┤Я»ЇЯ«еЯ«┐Я«▓Я»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї.
Я«цЯ«ЪЯ«ЋЯ«│Я«фЯ»Ї Я«фЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЋЯ«цЯ»Ї Я«цЯ»ЄЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»єЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ 15 Я««Я«ЙЯ«БЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«» Я«ЋЯ»ЂЯ«┤Я»ЂЯ«хЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«еЯ«┐Я«цЯ«┐Я«»Я»ЂЯ«цЯ«хЯ«┐ Я«хЯ«┤Я«ЎЯ»ЇЯ«ЋЯ«фЯ»Ї Я«фЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«фЯ«┤Я»ѕЯ«» Я««Я«ЙЯ«БЯ«хЯ«┐ Я«░Я«ЙЯ«юЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ«░Я»Ї Я«хЯ«┐Я«░Я»ЂЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ«ЙЯ«░Я»Ї. Я«ЁЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я«цЯ»Ђ Я«ЋЯ»ЂЯ«ЪЯ»ЂЯ««Я»ЇЯ«ф Я«хЯ«░Я»ЂЯ««Я«ЙЯ«ЕЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЅЯ«цЯ«х Я«хЯ«┐Я«░Я»ЂЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ«ЙЯ«░Я»Ї. Я«ЁЯ«еЯ»ЇЯ«ц 15 Я«ЋЯ»ЂЯ«ЪЯ»ЂЯ««Я»ЇЯ«фЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я«ЙЯ«ц Я«хЯ«░Я»ЂЯ««Я«ЙЯ«ЕЯ««Я»Ї Я«ЋЯ»ђЯ«┤Я»ЄЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
Рѓ╣3300, Рѓ╣5000, Рѓ╣4000, Рѓ╣4200, Рѓ╣3500, Рѓ╣4500, Рѓ╣3200, Рѓ╣3200, Рѓ╣4100, Рѓ╣4000, Рѓ╣4300, Рѓ╣3000, Рѓ╣3200, Рѓ╣4500, Рѓ╣4100.
Я«░Я«ЙЯ«юЯ««Я»Ї, Я««Я«ЙЯ«БЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ЂЯ«ЪЯ»ЂЯ««Я»ЇЯ«ф Я«хЯ«░Я»ЂЯ««Я«ЙЯ«ЕЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЈЯ«▒Я»ЇЯ«▒Я«хЯ«ЙЯ«▒Я»Ђ Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЋЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ«┐Я«░Я»ЂЯ««Я»ЇЯ«фЯ»ЂЯ«ЋЯ«┐Я«▒Я«ЙЯ«░Я»Ї.
Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї, Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«цЯ»Ђ.
Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ = Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї/15
=[3300+5000+4000+4200+3500+4500+3200+3200+4100+4000+4300+3000+3200+ 4500+4100]/15
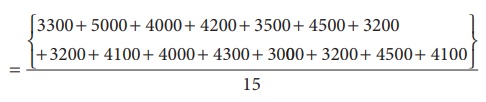
= 58100/15 = 3873.3
Рѓ╣3873.3 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЋЯ»ѕЯ«»Я»ѕ Я««Я«ЙЯ«БЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«ЕЯ»ѕЯ«хЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї, Я«ЁЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЪЯ»ѕЯ«» Я«ЋЯ»ЂЯ«ЪЯ»ЂЯ««Я»ЇЯ«ф Я«хЯ«░Я»ЂЯ««Я«ЙЯ«ЕЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«ЪЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«цЯ»Ђ Я«хЯ«┤Я«ЎЯ»ЇЯ«Ћ Я««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я«Й? Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є Рѓ╣3873.3 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ««Я«ЙЯ«Е Я«фЯ«┐Я«░Я«цЯ«┐Я«еЯ«┐Я«цЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«хЯ«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ѕЯ«»Я«Й? Я«ЄЯ«▓Я»ЇЯ«▓Я»ѕ, Я«ЄЯ«цЯ»Ђ Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«цЯ»Ђ. Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЋЯ»ЂЯ«ЪЯ»ЂЯ««Я»ЇЯ«ф Я«хЯ«░Я»ЂЯ««Я«ЙЯ«ЕЯ««Я»Ї Рѓ╣3000 Я«љЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«њЯ«░Я»Ђ Я««Я«ЙЯ«БЯ«хЯ«░Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«ЪЯ»ЂЯ««Я»ЇЯ«ф Я«хЯ«░Я»ЂЯ««Я«ЙЯ«ЕЯ««Я»Ї Рѓ╣5000 Я«љЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«њЯ«░Я»Ђ Я««Я«ЙЯ«БЯ«хЯ«░Я»ЂЯ««Я»Ї Я«њЯ«░Я»Є Я«цЯ»іЯ«ЋЯ»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЂЯ«хЯ«ЙЯ«░Я»ЇЯ«ЋЯ«│Я»Ї. Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я«ЙЯ«Е Я«ЄЯ«еЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ«┐Я«░Я«цЯ«┐Я«еЯ«┐Я«цЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«х Я«ЁЯ«│Я«хЯ»Ђ Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«хЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ.
Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ, Я««Я»ЂЯ«ЋЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«┐Я«ЪЯ«┐Я«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
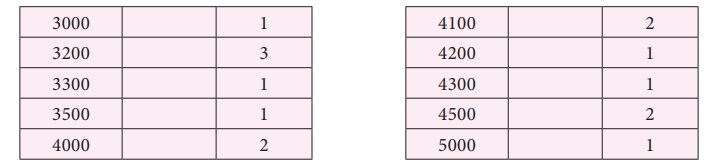
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є Я««Я»ЂЯ«ЋЯ«ЪЯ«ЙЯ«ЕЯ«цЯ»Ђ 3200 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«│Я»Ї Я«ЋЯ»ЂЯ«ЪЯ»ЂЯ««Я»ЇЯ«ф Я«хЯ«░Я»ЂЯ««Я«ЙЯ«ЕЯ««Я»Ї Рѓ╣3200 Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я««Я«ЙЯ«БЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«цЯ«┐Я«ЋЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«ЕЯ«░Я»Ї. Я«єЯ«ЋЯ«хЯ»Є Я«ЄЯ«цЯ»Ђ Я«еЯ««Я«цЯ»Ђ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«цЯ»Ђ.
Я«јЯ«ЕЯ«хЯ»Є, Я««Я»ЂЯ«ЋЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ««Я«ЙЯ«ЕЯ«цЯ«▓Я»ЇЯ«▓. Я«ЁЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«ЄЯ«еЯ»ЇЯ«ц Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«фЯ«┐Я«░Я«цЯ«┐Я«еЯ«┐Я«цЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«х Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ«хЯ«┐Я«░, Я«хЯ»ЄЯ«▒Я»Ђ Я«фЯ«┐Я«░Я«┐Я«цЯ«┐Я«еЯ«┐Я«цЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«х Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ«Й? Я«єЯ««Я»Ї, Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ, Я«цЯ«░Я«хЯ»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ«│Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«┐Я«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»іЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я««Я»ЂЯ«цЯ«▓Я«┐Я«▓Я»Ї Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЈЯ«▒Я»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ 3000, 3200, 3200, 3200, 3300, 3500, 4000, 4000, 4100, 4100, 4200, 4300, 4500, 4500, 5000.
Я«хЯ«░Я»ЂЯ««Я«ЙЯ«ЕЯ«цЯ»ЇЯ«цЯ»ѕ Я«ЈЯ«▒Я»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«цЯ»ЇЯ«цЯ«фЯ«┐Я«▒Я«ЋЯ»Ђ, Я«░Я«ЙЯ«юЯ««Я»Ї Я«ЁЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї, 8 Я«хЯ«цЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«Е Рѓ╣4000 Я«ЄЯ«цЯ»ЇЯ«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ«│Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«┐Я«░Я«┐Я«фЯ»ЇЯ«фЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«ЋЯ«┐Я«▒Я«ЙЯ«░Я»Ї. Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я««Я«ЙЯ«БЯ«хЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ«┤Я«ЎЯ»ЇЯ«ЋЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«┐Я«» Я«еЯ«┐Я«цЯ«┐ Я«ЅЯ«цЯ«хЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЁЯ«│Я«хЯ»ѕЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ««Я«ЙЯ«ЕЯ«┐Я«ЋЯ»ЇЯ«Ћ Я«ЄЯ«цЯ»Ђ Я«ЅЯ«цЯ«хЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. 4000 Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»Ї Я«ЄЯ«еЯ»ЇЯ«цЯ«цЯ»Ї Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«еЯ«ЪЯ»ЂЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Е Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«еЯ«ЪЯ»ЂЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Е Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«цЯ»Ї Я«цЯ»ЄЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»єЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«фЯ»єЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЄЯ«еЯ»ЇЯ«ц Я«хЯ«ЋЯ»ѕЯ«»Я«ЙЯ«Е Я«фЯ«┐Я«░Я«цЯ«┐Я«еЯ«┐Я«цЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«х Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я»Ї, Я«ЈЯ«▒Я»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЄЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«»Я»ЄЯ«▓Я«Й Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«еЯ«ЪЯ»ЂЯ«еЯ«┐Я«▓Я»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕ Я«ЁЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я»Ї 13, 14, 15, 16, 17 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 18 Я«єЯ«ЋЯ«┐Я«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«ЙЯ«Е, Я«ЄЯ«░Я»ЂЯ«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»іЯ«░Я»Ђ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«хЯ«ЕЯ«┐Я«»Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї. Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»ѕ Я«јЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«ЋЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«┐Я«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«цЯ»Ђ? Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ 6 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ»Ђ Я«ЊЯ«░Я»Ї Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є Я«еЯ«ЪЯ»ЂЯ«еЯ«┐Я«▓Я»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«ЙЯ«Ћ 3 Я«єЯ«хЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 4 Я«єЯ«хЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«Е. Я«єЯ«ЋЯ«хЯ»Є, Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ 3 Я«єЯ«хЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 4 Я«єЯ«хЯ«цЯ»Ђ Я«єЯ«ЋЯ«┐Я«» Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕ Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Ћ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ = 1/2 {3 Я«єЯ«хЯ«цЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ + 4 Я«єЯ«хЯ«цЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ}
= 1/2 {15 + 16}
= 15+16/2 = 31/2 = 15.5
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є, Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«┐Я«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ«░Я«хЯ«┐Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЈЯ«▒Я»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЄЯ«▒Я«ЎЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»І Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«░Я»Ї, Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«еЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«░ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«»Я«хЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«┐Я«ЪЯ«┐Я«ЋЯ»ЇЯ«Ћ,
i) Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЈЯ«▒Я»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЄЯ«▒Я«ЎЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»І Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
ii) Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ (n) Я«єЯ«ЕЯ«цЯ»Ђ Я«њЯ«▒Я»ЇЯ«▒Я»ѕ (Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ) Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«░Я»Ї (n+1/2) Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
iii) Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ (n) Я«єЯ«ЕЯ«цЯ»Ђ Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї (n/2) Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (n/2+1) Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»Є Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я««Я»ЂЯ«»Я«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ«ЙЯ«░Я»Ї
1. 3, 8, 7, 8, 4, 5, 6 Я«єЯ«ЋЯ«┐Я«» Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«еЯ«ЪЯ»ЂЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ :
Я«ЈЯ«▒Я»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї: 3, 4, 5, 6, 7, 8.8.
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є n = 7, Я«ЄЯ«цЯ»Ђ Я«њЯ«▒Я»ЇЯ«▒Я»ѕ Я«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї.
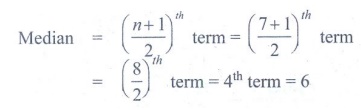
Я«јЯ«ЕЯ«хЯ»Є Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ 6.
2. 11, 14, 10, 9, 14, 11, 12, 6, 7, 7 Я«єЯ«ЋЯ«┐Я«» Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«еЯ«ЪЯ»ЂЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ :
Я«ЈЯ«▒Я»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї: 6, 7, 7, 9, 10, 11, 11, 12, 14, 14
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є is n = 10, Я«ЄЯ«цЯ»Ђ Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕ Я«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї..
Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ
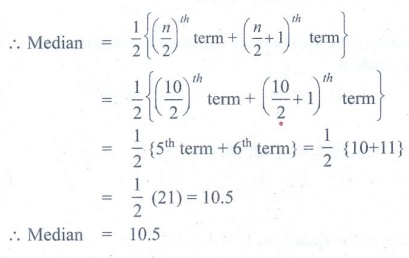
Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ = 10.5
Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
6 Я««Я»ЂЯ«цЯ«▓Я»Ї 7 Я««Я«ЙЯ«БЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЋЯ»ЂЯ«┤Я»ЂЯ«хЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐, Я«ЅЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я««Я«ЙЯ«БЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЪЯ»ѕЯ«» Я«јЯ«ЪЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«цЯ«░Я«хЯ»ѕЯ«џЯ»Ї Я«џЯ»ЄЯ«ЋЯ«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЋЯ»ЂЯ«┤Я»ЂЯ«хЯ«┐Я«▓Я»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐, Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, Я«ЋЯ»ЂЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЪЯ»ѕЯ«»Я»Є Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕ Я«њЯ«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї. Я«ЁЯ«хЯ»ѕ, Я«јЯ«▓Я»ЇЯ«▓Я«ЙЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Є Я««Я«ЙЯ«цЯ«┐Я«░Я«┐ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«Й?
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я««Я»ЂЯ«┤Я»Ђ Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«Ћ. Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЋЯ»ЂЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ЂЯ«ЪЯ«ЕЯ»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕ Я«њЯ«фЯ»ЇЯ«фЯ«┐Я«ЪЯ«хЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.10
Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«▓Я»ЇЯ«ЃЯ«фЯ»ЇЯ«хЯ«┐Я«│Я»ѕЯ«»Я«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї (Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я»Ї) Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї (Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»єЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї) Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«»Я«хЯ»ЂЯ««Я»Ї. 68, 79, 78, 65, 75, 70, 73.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЋЯ»ІЯ«▓Я»ЇЯ«ЃЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕ Я«ЈЯ«▒Я»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, 65, 68, 70, 73, 75, 78, 79.
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є n=7, Я«ЄЯ«цЯ»Ђ Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї.
Я«јЯ«ЕЯ«хЯ»Є Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ = ([n+1]/2) Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ
= ([7+1]/2) Я«єЯ«хЯ«цЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
= (8/2) Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ
= 4 Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
= 73
Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ 73 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.11
10 Я««Я«ЙЯ«БЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«ЪЯ»ѕЯ«ЋЯ«│Я»Ї (Я«ЋЯ«┐Я«▓Я»ІЯ«хЯ«┐Я«▓Я»Ї) Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. 35, 42, 40, 38, 25, 32, 29, 45, 20, 24. Я«ЁЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЪЯ»ѕЯ«» Я«јЯ«ЪЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«Ъ Я«▒Я«┐Я«»Я«хЯ»ЂЯ««Я»Ї.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ«хЯ«ЕЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«ЈЯ«▒Я»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
20, 24, 25, 29, 32, 35, 38, 40, 42, 45.
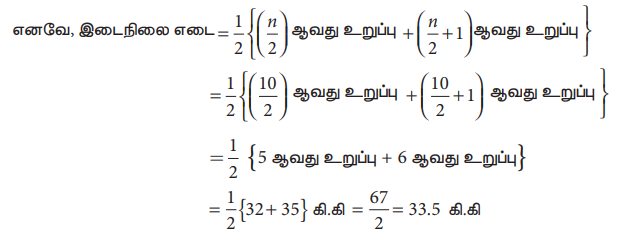
Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ Я«јЯ«ЪЯ»ѕ 33.5 Я«ЋЯ«┐.Я«ЋЯ«┐ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.12
Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ 16 Я«ЅЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ 12 Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«еЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«░ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«еЯ»ЇЯ«ц Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ 16 Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ 16 Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«еЯ»ЇЯ«цЯ«џЯ»Ї Я«џЯ»ІЯ«ЪЯ«┐ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЋЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«┐Я«ЪЯ«┐Я«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«ЁЯ«цЯ»Ђ 14 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 18 Я«јЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ»ѓЯ«▒Я«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ 16 Я«єЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2, 4, 7, 9, 12, 14, 18, 24, 28, 30, 45, 62 Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
Я«ЄЯ«еЯ»ЇЯ«цЯ«ЋЯ»Ї Я«ЋЯ»ЄЯ«│Я»ЇЯ«хЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ЄЯ«▒Я»ЇЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«фЯ«цЯ«┐Я«▓Я»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я««Я»Ї
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.13
11 Я«хЯ«ЋЯ»ѕЯ«»Я«ЙЯ«Е Я«јЯ«▓Я»ЇЯ«ѕЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї (Я«хЯ«ЙЯ«┤Я»ЇЯ«еЯ«ЙЯ«│Я»Ї) Я«єЯ«»Я»ЂЯ«ЪЯ»ЇЯ«ЋЯ«ЙЯ«▓Я««Я»Ї Я«еЯ«ЙЯ«ЪЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
365, 547, 730, 1095, 547, 912, 365, 1460, 1825, 1500, 2000. Я«јЯ«▓Я»ЇЯ«ѕЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ Я«єЯ«»Я»ЂЯ«ЪЯ»ЇЯ«ЋЯ«ЙЯ«▓Я«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«┐Я«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«цЯ«░Я«хЯ»ѕ Я«ЈЯ«▒Я»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї 365, 365, 547, 547, 730, 912, 1095, 1460, 1500, 1825, 2000. Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї (Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї) Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ 11 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї.
Я«јЯ«ЕЯ«хЯ»Є Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ Я«єЯ«ЕЯ«цЯ»Ђ (n+1/2) Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
= (11+1/2) Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ
= 6 Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ
Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ«ЙЯ«ЕЯ«цЯ»Ђ 912 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«▓Я»ЇЯ«ѕЯ«ЪЯ«┐ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»Ї Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ Я«єЯ«»Я»ЂЯ«ЪЯ»ЇЯ«ЋЯ«ЙЯ«▓Я««Я»Ї 912 Я«еЯ«ЙЯ«ЪЯ»ЇЯ«ЋЯ«│Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.14
Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«еЯ«ЪЯ»ЂЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«»Я«хЯ»ЂЯ««Я»Ї
12, 7, 23, 14, 19, 10, 5, 26.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЈЯ«▒Я»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї
5, 7, 10, 12, 14, 19, 23, 26
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є , n = 8, Я«ЄЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї.
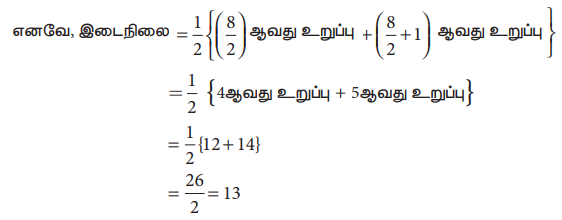
Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ 13 Я«єЯ«ЋЯ»ЂЯ««Я»Ї
Я«џЯ«┐Я«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«Ћ
Я«ЋЯ»ђЯ«┤Я»ЄЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ»ѓЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐ Я«џЯ»єЯ«»Я»ЇЯ«цЯ»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«ЋЯ»ЄЯ«│Я»ЇЯ«хЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«фЯ«цЯ«┐Я«▓Я«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
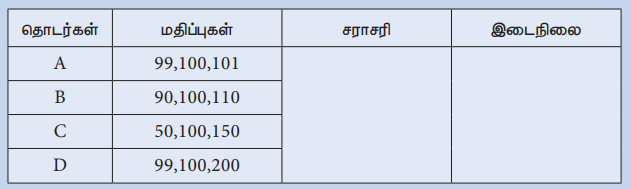
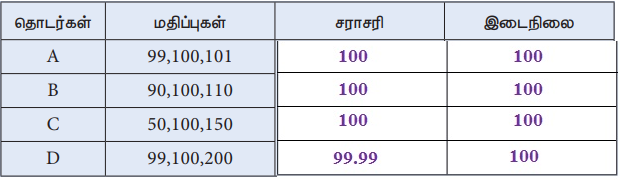
(i) Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Е Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї Я«»Я«ЙЯ«хЯ»ѕ?
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ : A, B Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї C.
(ii) 4 Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»Ђ Я«ЈЯ«ЕЯ»Ї Я«њЯ«░Я»Є Я««Я«ЙЯ«цЯ«┐Я«░Я«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ?
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ: Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ 100Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї .
(iii) A,B Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї C Я«єЯ«ЋЯ«┐Я«» Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«јЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐Я«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я««Я«ЙЯ«▒Я«ЙЯ««Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ: Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я«ЙЯ«Е Я«хЯ»ЄЯ«▒Я»ЂЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«џЯ««Я««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«┐Я«ЕЯ«ЙЯ«▓Я»Ї .
(iv) Я«цЯ«░Я«хЯ«┐Я«▓Я»Ї Я«јЯ«ЕЯ»ЇЯ«Е Я««Я«ЙЯ«▒Я»ЇЯ«▒Я««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«цЯ«ЙЯ«▓Я»Ї D Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«│Я«хЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ: 99Я«љ 0 Я«хЯ«ЙЯ«Ћ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ 200Я«љ 101 Я«єЯ«Ћ Я««Я«ЙЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ«ЙЯ«▓Я»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ 100Я«єЯ«Ћ Я««Я«ЙЯ«▒Я»ЂЯ««Я»Ї .