முகடு

முகடு

கூட்டுச் சராசரி என்பது தரவுகளின் மையப்போக்கின் பிரதிநிதித்துவ மதிப்பு அல்லது மையப்போக்கு அளவீடுகளில் ஒன்றாகும் என்பதை நாம் முன்பு விவாதித்தோம். தரவுகள் மற்றும் அதன் நோக்கத்தைப் பொறுத்து மையப்போக்கின் பிற அளவீட்டு முறைகளும் பயன்படுத்தப்படலாம். உதாரணமாக, ஒரு வாரத்திற்கு ஒரு கடையில் வெவ்வேறு அளவிலான காலணிகளின் விற்பனை விவரங்களைக் கவனியுங்கள்

கடைக்காரர் வார இறுதியில் தன்னிடமுள்ள இருப்பு விவரங்களைக் கணக்கிடவேண்டும். விற்கப்பட்ட காலணிகளின் எண்ணிக்கையைக் கூட்டுச் சராசரியைக் கொண்டு கண்டுபிடிப்பதாக வைத்துக்கொள்வோம்.

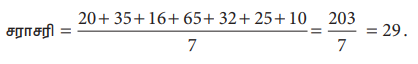
சராசரி = [ 20+35+16+65+32+25+10]/7 = 203/7 = 29.

இங்கே காலணிகளின் சராசரி எண்ணிக்கை 29 எனக் கணக்கிட்டுள்ளோம். இதன் பொருள் கடைக்காரர் ஒவ்வொரு அளவிலும் 29 சோடி காலணிகளைப் பெறவேண்டும். இப்படி முடிவெடுப்பது புத்திசாலித்தனமா?

அதிகபட்சமாக வாங்கவேண்டிய காலணிகளின் அளவு 8 அங்குலத்தில்தான் உள்ளது என்பதைக் கவனிக்க வேண்டும். எனவே, கடைக்காரர் 8 அங்குல அளவுள்ள காலணிகளை அதிக அளவில் பெறவேண்டும். எனவே கூட்டுச் சராசரியானது இந்த நோக்கத்திற்குப் பொருந்தாது. இங்கே நமக்கு ‘முகடு' எனப்படும் தரவின் மற்றொரு வகையான பிரதிநிதித்துவ மதிப்பீடு தேவைப்படுகிறது.

'முகடு' என்பது அதிகபட்ச எண்ணிக்கையில் நிகழும் தரவுகளின் மதிப்பாகும். 

மற்றொரு உதாரணத்தைக் கவனிக்கவும்,

ஒரு கடைக்காரர் தேவைக்கேற்ப இருப்பு விவரங்களைத் திட்டமிட ரெடிமேட் (ஆயத்த) சட்டைகளின் விற்பனையைக் கூர்ந்து ஆய்வு செய்கிறார். விற்பனையான ரெடிமேட் (ஆயத்த) சட்டைகளின் விவரங்கள் கீழேக் கொடுக்கப்பட்டுள்ளன. 

சட்டைகளின் அளவுகளான 30" மற்றும் 34" ஆகியவைகளுக்குச் சமமான தேவை இருப்பதை இங்கே அவர் கவனிக்கிறார். இப்போது இத்தரவுகள் இரண்டு முகடுகளைக் கொண்டுள்ளன. ஏனெனில், இத்தரவுகளில் இரண்டு அதிகபட்ச நிகழ்வுகள் உள்ளன. இந்த இரண்டு அளவுகளான 30" மற்றும் 34" ரெடிமேட் (ஆயத்த) சட்டைகளை அவர் இருப்பில் வைத்துக்கொள்ள ஆயத்தப்படுகிறார். இந்தத் தரவு இரண்டு முகடுகளைக் கொண்டுள்ளது என்பதை நினைவில் கொள்க. எனவே, இது இருமுகடுகளின் தரவு என்று அழைக்கப்படுகிறது.

முயன்று பார் 

(1) பின்வரும் தரவுகளைக் கொண்டு முகடு காண்க. 

    2, 6, 5, 3, 0, 3, 4, 3, 2, 4, 5, 2 

தீர்வு :

கொடுக்கப்பட்ட எண்களை ஏறுவரிசையில் அமைத்தால், நமக்குப் பின்வருமாறு எண்கள் கிடைக்கும். 0, 2, 2, 2, 3, 3, 3,4, 4, 5, 5, 6

இந்தத் தரவுகளின் முகடு  2 மற்றும்  3 ஆகும். ஏனெனில் இது மற்ற தரவுகளை விட அதிக எண்ணிக்கையில் நிகழ்கிறது.

(2) பின்வரும் தரவுகளின் முகடு காண்க. 

 3, 12, 15, 3, 4, 12, 11, 3, 12, 9, 19 

தீர்வு :

கொடுக்கப்பட்ட எண்களை ஏறுவரிசையில் அமைத்தால், நமக்குப் பின்வருமாறு எண்கள் கிடைக்கும் : 3, 3, 3, 4, 9, 11, 12, 12, 12, 15, 19.

இந்தத் தரவுகளின் முகடு  3 மற்றும்  12 ஆகும். ஏனெனில் இது மற்ற தரவுகளை விட அதிக எண்ணிக்கையில் நிகழ்கிறது.

(3) 20 க்குள் உள்ள இரட்டை எண்களின் முகடு காண்க.

தீர்வு :

20இல்  உள்ள இரட்டை எண்கள் 2,4, 6, 8, 10, 12. 14. 16, 18.

இந்தத் தரவுகளில் எந்த முகடும் இல்லை . 

எடுத்துக்காட்டு 5.5   

கொடுக்கப்பட்ட எண்களின் முகடு காண்க.

5, 7, 10, 12, 4, 5, 3, 10, 3, 4, 5, 7, 9, 10, 5, 12, 16, 20, 5 

தீர்வு

எந்த மதிப்பையும் விட்டுவிடாமல் எண்களை ஏறு வரிசையில் அமைக்கவும். நமக்குப் பின்வருமாறு எண்கள் கிடைக்கும்.

3, 3, 4, 4, 5, 5, 5, 5, 5, 7, 7, 9, 10, 10, 10, 12, 12, 16, 20

இந்தத் தரவுகளின் முகடு 5 ஆகும். ஏனெனில் இது மற்ற தரவுகளை விட அதிக எண்ணிக்கையில் நிகழ்கிறது.

குறிப்பு 

‘முகடு’ கண்டுபிடிக்கக் கொடுக்கப்பட்ட தரவுகளை ஏறுவரிசையில் அமைப்பது கட்டாயமில்லை. 'முகடு' காணுவதற்கு ஒவ்வொரு மதிப்பையும் கணக்கில் எடுத்துக்கொள்ளப்படுவதை உறுதிப்படுத்த உதவுவதோடு முகடின் மதிப்பை எளிதில் அடையாளம் காணவும் இது உதவுகிறது.

எடுத்துக்காட்டு 5.6 

ஒரு தேர்வில் ஒரு வகுப்பிலுள்ள 11 மாணவர்கள் பெற்ற மதிப்பெண்கள் கீழேக் கொடுக்கப்பட்டுள்ளன 23, 2, 15, 38, 21, 19, 23, 23, 26, 34, 23. இம்மதிப்பெண்களின் முகடு காண்க.

தீர்வு 

கொடுக்கப்பட்ட மதிப்பெண்களை ஏறுவரிசையில் அமைத்தால், நமக்குப் பின்வருமாறு எண்கள் கிடைக்கும்.

2, 15, 19, 21, 23, 23, 23, 23, 26, 34, 38.

இங்கு தெளிவாக, 23 என்பதே அதிகபட்ச எண்ணிக்கையில் நிகழ்கிறது. எனவே, மதிப்பெண்களின் முகடு '23' ஆகும்.

எடுத்துக்காட்டு 5.7   

பின்வரும் தரவுகளின் முகடு காண்க. 123, 132, 145, 176, 180, 120

தீர்வு

கொடுக்கப்பட்ட தரவுகளிலிருந்து எந்தவொரு மதிப்பும் மீண்டும் மீண்டும் வரவில்லை என்பதைக் காணலாம். இங்கு ஒவ்வொரு மதிப்பும் ஒரு முறை மட்டுமே உள்ளது. எனவே, இதில் முகடே இல்லை.

குறிப்பு 

ஒவ்வொரு மதிப்பும் ஒரு முறை மட்டுமே நிகழ்ந்தால், அந்த தரவுகளுக்கு எந்த முகடும் இல்லை. 

சிந்திக்க

1. குழந்தைகளுக்காகப் பலவிதமான பொம்மைகளை உருவாக்கும் ஒரு பொம்மை தொழிற்சாலை, எல்லாக் குழந்தைகளும் விரும்பக்கூடிய மிகப் பிரபலமான பொம்மையை அறிய விரும்புகிறது. எந்தச் சராசரி அதற்கு மிகவும் பொருத்தமானதாக இருக்கும்? 

தீர்வு : முகடு

2. 20 இக்கும் 40 இக்கும் இடையிலுள்ள ஒற்றை எண்களில் ஏதேனும் முகடு உள்ளதா? விவாதிக்க.

தீர்வு :  20 முதல்  40 வரையிலான ஒற்றை படை எண்கள் 21, 23, 25, 27, 29, 31, 33, 35, 37, 39.

இங்கு ஒவ்வொரு மதிப்பும் ஒரு முறை மட்டுமே உள்ளது. எனவே, இதில் முகடு இல்லை.

1. அதிகமான தரவுகளின் முகடு

தரவுகளின் எண்ணிக்கை அதிகமாக இருக்கும்போது நிகழும் மதிப்பை அடையாளம் காண்பது எளிதானதல்ல. அவ்வாறான நிலையில், நேர்க்கோட்டுக் குறிகளைப் பயன்படுத்தித் தரவுகளைக் குழுக்களாகப் பிரித்துப் பின்னர் முகடைக் கண்டுபிடிக்கலாம்.

25 போட்டிகளில் ஒரு கால்பந்து அணி அடித்த கோல்களின் எண்ணிக்கையை எடுத்துக்கொள்க. அவ்வணி அடித்த கோல்கள் ஆனது, 1, 3, 2, 5, 4, 6, 2, 2, 2, 4, 6, 4, 3, 2, 1, 1, 4, 5, 3, 2, 2, 4, 3, 0, 1 ஆக இருக்கிறது.

இந்தத் தரவுகளின் முகடைக் காண்பதற்கு, அடித்த கோல்களின் எண்ணிக்கையை அட்டவணையில் குறிக்கவும். கோல்களின் எண்ணிக்கை 0 வில் ஆரம்பித்து அதிகபட்சமாக 6 இல் முடிவடைகிறது.

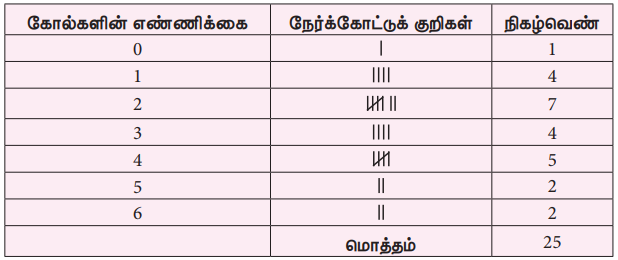
அட்டவணையிலிருந்து, நாம் கவனிப்பது, 2 கோல்கள் அதிகபட்சமாக இருமுறை நிகழ்கிறது என்பதை அறியலாம். இதில் அதிகபட்சநிகழ்வெண்ணான 7 உடன் ஒத்த மதிப்பு 2 ஆகும். எனவே முகடு '2' ஆகும்.

எடுத்துக்காட்டு 5.8   

பின்வரும் தரவுகளின் முகடைக் காண்க . 14, 15, 12, 14, 16, 15, 17, 13, 16, 16, 15, 12, 16, 15, 13, 14, 15, 13, 15, 17, 15, 14, 18, 19, 12, 14, 15, 16, 15, 16, 13, 12. 

தீர்வு

நாம் தரவுகளைப் பின்வருமாறு அட்டவணைப்படுத்துவோம். 

மொத்தத் தரவுகளும் 12 முதல் 19 வரை இருக்கிறது.

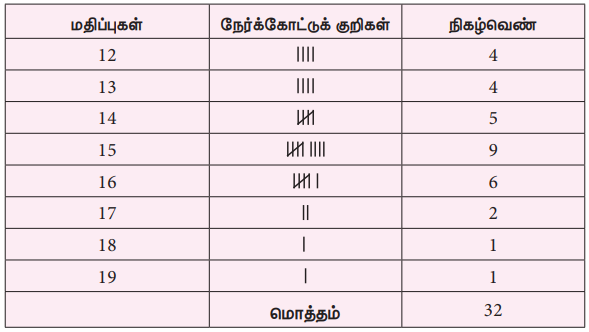
அதிக பட்ச நிகழ்வெண்ணான 9 ஆனது 15 என்ற மதிப்புடன் ஒத்திருக்கிறது. எனவே, இந்தத் தரவுகளின் முகடு 15 ஆகும்.

எடுத்துக்காட்டு 5.9 

மாணவர்கள் படிப்பதற்காக எத்தனை மணிநேரம் எடுத்துக்கொண்டனர் என்பதைப் பின்வரும் தரவுகள் காட்டுகிறது.

முகடு காண்க. 

தீர்வு

அதிகபட்சமாகப்படிக்கும் நேரத்தை 4 மாணவர்கள் ஒருமணி நேரமாக எடுத்துக் கொண்டதால், இத்தரவின் முகடு 1 மணி நேரம் ஆகும்.

சிந்திக்க 

பின்வரும் பொருள்களை உற்பத்திசெய்யும் நிறுவனங்களுக்கு எந்தச் சராசரி பொருத்தமானதாக இருக்கும்? ஏன்? 

(i) நாட்குறிப்பேடுகளும் குறிப்பேடுகளும்.

(ii) பள்ளிப் பைகள். 

(iii) கால்சட்டை மற்றும் மேல்சட்டைகள்.

தீர்வு : மேலே உள்ள அனைத்து சராசரியும் பொருத்தமானதாக இருக்கும்