Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ, Я«ЁЯ«цЯ«ЕЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї - Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»їЯ«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї | 11th Physics : UNIT 7 : Properties of Matter
11Я«хЯ«цЯ»Ђ Я«ЄЯ«»Я«▒Я»ЇЯ«фЯ«┐Я«»Я«▓Я»Ї : Я«ЁЯ«▓Я«ЋЯ»Ђ 7 : Я«фЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ»іЯ«░Я»ЂЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї
Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»їЯ«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї
Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»їЯ«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї
Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я«┐Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ«« Я«еЯ«┐Я«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«хЯ»ђЯ«цЯ«цЯ»ЇЯ«цЯ»ѕ Я«ЁЯ«▒Я«┐Я«» Я«еЯ»ђЯ«░Я»ЇЯ««Я««Я»Ї Я«фЯ«ЙЯ«»Я»ЇЯ«хЯ«цЯ»Ђ Я«џЯ»ђЯ«░Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«еЯ»ђЯ«░Я»ЇЯ««Я««Я»Ї Я«фЯ«ЙЯ«»Я»ЇЯ«хЯ«цЯ»Ђ Я«џЯ»ђЯ«░Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»єЯ«ЕЯ«┐Я«▓Я»Ї Я«фЯ«ЙЯ«»Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я»ЂЯ««Я»Ї Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»іЯ«▒Я»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«»Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«» Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЊЯ«ЪЯ»ЇЯ«ЪЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ЇЯ«џЯ»ђЯ«░Я»Ї Я«ЊЯ«ЪЯ»ЇЯ«ЪЯ««Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.
Я«џЯ»ђЯ«░Я«▒Я»ЇЯ«▒ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ a1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a2 Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ a1 > a2. Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ AB Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«Ћ. Я«фЯ«ЙЯ«ЋЯ»ЂЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я«ЁЯ««Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я«ЙЯ«ц Я«еЯ»ђЯ«░Я»ЇЯ««Я««Я»Ї Я«џЯ»ђЯ«░Я«ЙЯ«Ћ v1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї v2 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є a1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a2 Я«фЯ«░Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ«┤Я«┐Я«»Я»Є Я«фЯ«ЪЯ««Я»Ї 7.32 Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«фЯ«ЙЯ«»Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
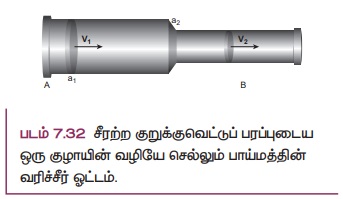
╬ћt Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«ЙЯ«▓ Я«ЁЯ«│Я«хЯ«┐Я«▓Я»Ї A Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ«┐Я«▒Я»ѕ m1 Я«јЯ«ЕЯ«┐Я«▓Я»Ї m1 = (a1v1 ╬ћt) ¤Ђ
╬ћt Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«ЙЯ«▓ Я«ЁЯ«│Я«хЯ«┐Я«▓Я»Ї B Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ«┐Я«▒Я»ѕ m2 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, m2 = (a2v2 ╬ћt) ¤Ђ
Я«ЁЯ««Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я«ЙЯ«ц Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«еЯ«┐Я«▒Я»ѕ Я««Я«ЙЯ«▒Я«ЙЯ«цЯ»Ђ m1 = m2
a1 v1 ╬ћt ¤Ђ = a2 v2 ╬ћt ¤Ђ
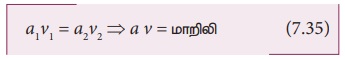
Я«ЄЯ«цЯ»ЂЯ«хЯ»Є Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ, Я«фЯ«ЙЯ«»Я»ЂЯ««Я»Ї Я«фЯ«ЙЯ«»Я»ЇЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«еЯ«┐Я«▒Я»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я««Я«ЙЯ«▒Я«ЙЯ««Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ av = Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐, Я«ЄЯ«цЯ«ЕЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«│Я»Ї Я«фЯ«░Я»ЂЯ««Я«фЯ»ЇЯ«фЯ«ЙЯ«»Я««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«фЯ«ЙЯ«»Я»ЂЯ««Я»Ї Я«хЯ»ђЯ«цЯ««Я»Ї Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я»Ї Я««Я»ЂЯ«┤Я»ЂЯ«хЯ«цЯ»ЂЯ««Я»Ї Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я««Я«ЙЯ«▒Я«ЙЯ«Ћ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«хЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«фЯ«ЙЯ«»Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ««Я»Ї Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 7.14
Я«њЯ«░Я»Ђ Я«џЯ«ЙЯ«цЯ«ЙЯ«░Я«Б Я««Я«ЕЯ«┐Я«цЯ«ЕЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«еЯ«ЙЯ«ЪЯ«┐ Я«хЯ«┤Я«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я«цЯ»ЇЯ«цЯ««Я»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«хЯ»ЄЯ«ЋЯ««Я»Ї 0.33 ms-1. (Я«єЯ«░Я««Я»Ї r = 0.8 cm) Я«фЯ»єЯ«░Я»ЂЯ«еЯ«ЙЯ«ЪЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 0.4 cm Я«єЯ«░Я««Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ 30 Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«фЯ»єЯ«░Я»ЂЯ««Я»Ї Я«цЯ««Я«ЕЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«░Я«цЯ»ЇЯ«цЯ««Я»Ї Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«цЯ««Я«ЕЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«ЄЯ«░Я«цЯ»ЇЯ«цЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
a1v1 = 30 a2 v2 РЄњ ¤ђ r12v1 = 30 ¤ђ r22v2
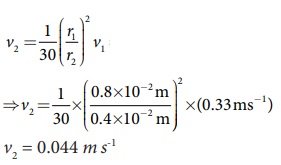
Я«еЯ»ђЯ«░Я»ЇЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц, Я«ЄЯ«»Я«ЋЯ»ЇЯ«Ћ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ«┐Я«▓Я»ѕ Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї
Я«џЯ»ђЯ«░Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«ЙЯ«»Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ѓЯ«хЯ«ЋЯ»ѕЯ«»Я«ЙЯ«Е Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»ЇЯ«ЋЯ«│Я»Ї Я«ЅЯ«БЯ»ЇЯ«ЪЯ»Ђ. Я«ЁЯ«хЯ»ѕ 1) Я«ЄЯ«»Я«ЋЯ»ЇЯ«Ћ Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї 2) Я«еЯ«┐Я«▓Я»ѕ Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 3) Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
1. Я«ЄЯ«»Я«ЋЯ»ЇЯ«Ћ Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї : m Я«еЯ«┐Я«▒Я»ѕЯ«»Я»ЂЯ««Я»Ї v Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ««Я»ЂЯ««Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«»Я«ЋЯ»ЇЯ«Ћ Я«єЯ«▒Я»ЇЯ«▒Я«▓Я«ЙЯ«ЕЯ«цЯ»Ђ
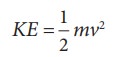
Я«ЊЯ«░Я«▓Я«ЋЯ»Ђ Я«еЯ«┐Я«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ЄЯ«»Я«ЋЯ»ЇЯ«Ћ Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї =
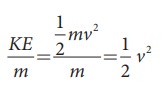
Я«ЄЯ«цЯ»ЄЯ«фЯ»ІЯ«▓Я»Ї, Я«ЊЯ«░Я«▓Я«ЋЯ»Ђ Я«фЯ«░Я»ЂЯ««Я«ЕЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ЄЯ«»Я«ЋЯ»ЇЯ«Ћ Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї
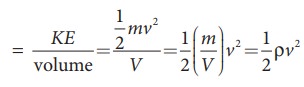
2. Я«еЯ«┐Я«▓Я»ѕЯ«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї: Я«цЯ«░Я»ѕЯ««Я«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ h Я«ЅЯ«»Я«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ m Я«еЯ«┐Я«▒Я»ѕЯ«ЋЯ»іnЯ«БЯ»ЇЯ«Ъ Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«▒Я»ЇЯ«▒Я«▓Я»Ї
PE = mgh
Я«ЊЯ«░Я«▓Я«ЋЯ»Ђ Я«еЯ«┐Я«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«▒Я»ЇЯ«▒Я«▓Я»Ї
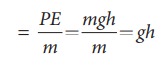
Я«ЄЯ«цЯ»ЄЯ«фЯ»ІЯ«▓Я»Ї Я«ЊЯ«░Я«▓Я«ЋЯ»Ђ Я«фЯ«░Я»ЂЯ««Я«ЕЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«▒Я»ЇЯ«▒Я«▓Я»Ї
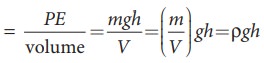
3. Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї: Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ЇЯ««Я»ђЯ«цЯ»Ђ Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ«цЯ»ЇЯ«цЯ»ѕЯ«џЯ»Ї Я«џЯ»єЯ«▓Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«хЯ«цЯ«ЙЯ«▓Я»Ї
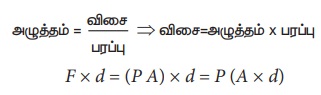
Я«јЯ«ЕЯ«хЯ»Є Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї EP = PV
Я«ЊЯ«░Я«▓Я«ЋЯ»Ђ Я«еЯ«┐Я«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї
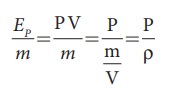
Я«ЄЯ«цЯ»ЄЯ«фЯ»ІЯ«▓Я»Ї Я«ЊЯ«░Я«▓Я«ЋЯ»Ђ Я«фЯ«░Я»ЂЯ««Я«ЕЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї
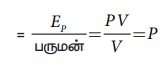
Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї
1738 Я«єЯ««Я»Ї Я«єЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«џЯ»ЂЯ«хЯ«┐Я«ИЯ»Ї Я«еЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЁЯ«▒Я«┐Я«хЯ«┐Я«»Я«▓Я»Ї Я«ЁЯ«▒Я«┐Я«ъЯ«░Я»Ї Я«ЪЯ»ЄЯ«ЕЯ«┐Я«»Я«▓Я»Ї Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐ Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ«░Я»Ї Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«хЯ«░Я«┐Я«џЯ»ЇЯ«џЯ»ђЯ«░Я»Ї Я«ЊЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ѕ Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«░Я»Ї. Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї Я««Я«ЙЯ«▒Я«Й Я«хЯ«┐Я«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ«хЯ«░Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«хЯ«░Я«┐Я«џЯ»ЇЯ«џЯ»ђЯ«░Я»Ї Я«ЊЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ѕЯ«цЯ»Ї Я«цЯ«░Я»ЂЯ«хЯ«┐Я«цЯ»ЇЯ«цЯ«ЙЯ«░Я»Ї.
Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї
Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐ Я«хЯ«░Я«┐Я«џЯ»ЇЯ«џЯ»ђЯ«░Я»Ї Я«ЊЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ««Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я«ЙЯ«ц, Я«фЯ«ЙЯ«ЋЯ»ЂЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«▒Я»ЇЯ«▒, Я«ЊЯ«░Я«▓Я«ЋЯ»Ђ Я«еЯ«┐Я«▒Я»ѕЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї, Я«ЄЯ«»Я«ЋЯ»ЇЯ«Ћ Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«▒Я»ЇЯ«▒Я«▓Я»Ї Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЋЯ»ѕ Я«јЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»ЂЯ««Я»Ї Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЋЯ«БЯ«┐Я«цЯ««Я»ЂЯ«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐
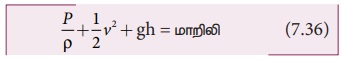
Я«ЄЯ«цЯ»ЂЯ«хЯ»Є Я«фЯ»єЯ«░Я»ЇЯ«│Я»єЯ«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«цЯ»ЇЯ«цЯ«▓Я»Ї :

Я«фЯ«ЪЯ««Я»Ї 7.33 Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ AB Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я«┐Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я«ЙЯ«Ћ Я«еЯ»ђЯ«░Я»ЇЯ««Я««Я»Ї Я«фЯ«ЙЯ«»Я»ЇЯ«хЯ«цЯ«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ V Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«ЕЯ»ѕ A Я«хЯ«┤Я«┐Я«»Я«ЙЯ«Ћ t Я«ЋЯ«ЙЯ«▓Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«еЯ»ЂЯ«┤Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«░Я»ЂЯ««Я«ЕЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я««Я»ЂЯ«ЕЯ»ѕ B Я«хЯ«┤Я«┐Я«»Я«ЙЯ«Ћ Я«ЁЯ«цЯ»Є Я«ЋЯ«ЙЯ«▓Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«хЯ»єЯ«│Я«┐Я«»Я»ЄЯ«▒Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«░Я»ЂЯ««Я«ЕЯ»ЂЯ««Я»Ї V Я«єЯ«ЋЯ»ЂЯ««Я»Ї. aA, vA Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї PA Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ»ѕ A Я«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я«┐Я«ЕЯ»Ї Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ, Я«еЯ»ђЯ«░Я»ЇЯ«« Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ«« Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ««Я»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«Ћ.
A Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«еЯ»ђЯ«░Я»ЇЯ««Я««Я»Ї Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«хЯ«┐Я«џЯ»ѕ
FA = PAaA
t Я«ЋЯ«ЙЯ«▓ Я«ЁЯ«│Я«хЯ«┐Я«▓Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я««Я»Ї Я«ЋЯ«ЪЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ
d = vA t
Я«јЯ«ЕЯ«хЯ»Є Я«џЯ»єЯ«»Я»ЇЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«хЯ»ЄЯ«▓Я»ѕ
W = FAd = PAaAvA t
Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї aAvAt = aAd =V, A Я«ЄЯ«▓Я»Ї Я«еЯ»ЂЯ«┤Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«░Я»ЂЯ««Я«ЕЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є Я«џЯ»єЯ«»Я»ЇЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«хЯ»ЄЯ«▓Я»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ A Я«ЄЯ«▓Я»Ї Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«єЯ«▒Я»ЇЯ«▒Я«▓Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
W = FAd = PAV
A Я«ЄЯ«▓Я»Ї Я«ЊЯ«░Я«▓Я«ЋЯ»Ђ Я«фЯ«░Я»ЂЯ««Я«ЕЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї

A Я«ЄЯ«▓Я»Ї Я«ЊЯ«░Я«▓Я«ЋЯ»Ђ Я«еЯ«┐Я«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї =
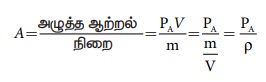
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ m Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї A Я«ЄЯ«▓Я»Ї Я«еЯ»ЂЯ«┤Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ«┐Я«▒Я»ѕ. Я«јЯ«ЕЯ«хЯ»Є A Я«ЄЯ«▓Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї
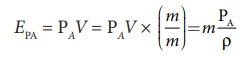
A Я«ЄЯ«▓Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«▒Я»ЇЯ«▒Я«▓Я»Ї
PEA = mg hA,
A Я«ЄЯ«▓Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ«« Я«ЊЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЋЯ«ЙЯ«░Я«БЯ««Я«ЙЯ«Ћ Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«»Я«ЋЯ»ЇЯ«Ћ Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї
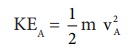
Я«јЯ«ЕЯ«хЯ»Є A Я«ЄЯ«▓Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ«« Я«ЊЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ«ЙЯ«▓Я»Ї Я««Я»іЯ«цЯ»ЇЯ«ц Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї
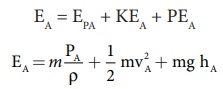
Я«ЄЯ«цЯ»ЄЯ«фЯ»ІЯ«▓Я»Ї aB, vB, Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї PB Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ»ѕ Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є B Я«ЄЯ«▓Я»Ї Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я«┐Я«ЕЯ»Ї Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ, Я«еЯ»ђЯ«░Я»ЇЯ«« Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«░Я»ЇЯ«« Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ.
B Я«ЄЯ«▓Я»Ї Я««Я»іЯ«цЯ»ЇЯ«ц Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї
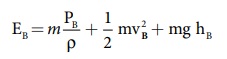
Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї Я««Я«ЙЯ«▒Я«Й Я«хЯ«┐Я«цЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ
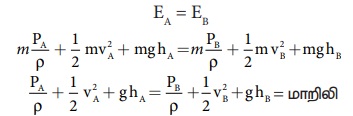
Я««Я»ЄЯ«▓Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
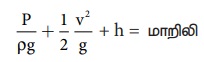
Я««Я»ЄЯ«▓Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї Я««Я«ЙЯ«▒Я«Й Я«хЯ«┐Я«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«хЯ«┐Я«│Я»ѕЯ«хЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЅЯ«░Я«ЙЯ«»Я»ЇЯ«хЯ«┐Я«ЕЯ«ЙЯ«▓Я»Ї Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї Я«ЄЯ«┤Я«фЯ»ЇЯ«фЯ»Ђ Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ«ЙЯ«цЯ«хЯ«░Я»ѕ Я«ЄЯ«џЯ»ЇЯ«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я««Я»єЯ«»Я»ЇЯ«»Я«ЙЯ«ЕЯ«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ , Я«еЯ»ђЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЈЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«џЯ»єЯ«▓Я»ЇЯ«хЯ«цЯ«ЙЯ«▓Я»Ї Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▒Я»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«»Я»Є Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЅЯ«░Я«ЙЯ«»Я»ЇЯ«хЯ»Ђ Я«хЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«ЕЯ«ЙЯ«▓Я»Ї Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї Я«ЄЯ«┤Я«фЯ»ЇЯ«фЯ»Ђ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«цЯ»ЇЯ«цЯ«ЋЯ»ѕЯ«» Я«єЯ«▒Я»ЇЯ«▒Я«▓Я»Ї Я«ЄЯ«┤Я«фЯ»ЇЯ«фЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ Я«хЯ»єЯ«фЯ»ЇЯ«ф Я«єЯ«▒Я»ЇЯ«▒Я«▓Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЇЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ«ЙЯ«ЕЯ«цЯ»Ђ, Я«џЯ»ЂЯ«┤Я«┐ Я«фЯ«ЙЯ«ЋЯ»ЂЯ«еЯ«┐Я«▓Я»ѕЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«фЯ«ЙЯ«ЋЯ»ЂЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я«еЯ»ђЯ«░Я»ЇЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»ЂЯ««Я»Ї. Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«Ћ Я«еЯ»ђЯ«░Я»ЇЯ««Я««Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«цЯ»ЇЯ«цЯ«│Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я»Ї Я«хЯ«┤Я«┐Я«»Я»Є Я«хЯ»єЯ«│Я«┐Я«»Я»ЄЯ«▒Я«┐Я«ЕЯ«ЙЯ«▓Я»Ї
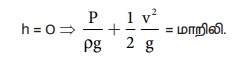
Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐ Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
(Я«Ё) Я«џЯ»ѓЯ«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«ЋЯ»ѓЯ«░Я»ѕЯ«ЋЯ«│Я»Ї Я«цЯ»ѓЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«јЯ«▒Я«┐Я«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї
Я««Я»ЂЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«хЯ»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЋЯ»ЂЯ«ЪЯ«┐Я«џЯ»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ»ѓЯ«░Я»ѕЯ«ЋЯ«│Я»Ї Я«фЯ«ЪЯ««Я»Ї 7.34 Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«џЯ«ЙЯ«»Я»ЇЯ«хЯ«ЙЯ«Ћ Я«хЯ«ЪЯ«┐Я«хЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«Е. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я««Я«ЙЯ«Е Я«ЁЯ«▒Я«┐Я«хЯ«┐Я«»Я«▓Я»Ї Я«ЋЯ«ЙЯ«░Я«БЯ««Я»Ї Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ«цЯ»ЇЯ«цЯ»ЂЯ«хЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐ Я«ЁЯ««Я»ѕЯ«хЯ«цЯ«ЙЯ«▓Я»Ї Я«хЯ»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«џЯ»ѓЯ«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«▒Я»ЇЯ«▒Я»Ђ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«фЯ»ЂЯ«»Я«▓Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«фЯ«ЙЯ«цЯ»ЂЯ«ЋЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е.
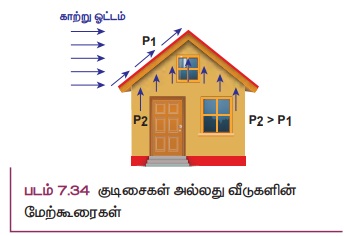
Я«фЯ»ЂЯ«»Я«▓Я»ЇЯ«ЋЯ«ЙЯ«▒Я»ЇЯ«▒Я»Ђ Я«хЯ»ђЯ«џЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒ Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»ЄЯ«цЯ««Я»Ї Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ«ЙЯ«хЯ«БЯ»ЇЯ«БЯ««Я»Ї Я«ЋЯ»ЂЯ«ЪЯ«┐Я«џЯ»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«░Я»ѕЯ«ЋЯ«│Я»Ї Я«цЯ»ѓЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«јЯ«▒Я«┐Я«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«ЁЯ«цЯ«┐Я«хЯ»ЄЯ«ЋЯ««Я«ЙЯ«Ћ Я«хЯ»ђЯ«џЯ»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«▒Я»ЇЯ«▒Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЋЯ»ѓЯ«░Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»Є P1 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«еЯ»ЇЯ«ц Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ«цЯ»ЇЯ«цЯ»ѕ Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЋЯ»ѓЯ«░Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ»ђЯ«┤Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ P2 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ««Я»Ї Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«хЯ»ЄЯ«▒Я»ЂЯ«фЯ«ЙЯ«ЪЯ»Ђ (P1 - P2) Я««Я»ЄЯ«▓Я»ЇЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«ЅЯ«еЯ»ЇЯ«цЯ»Ђ Я«хЯ«┐Я«џЯ»ѕЯ«»Я»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЋЯ»ѓЯ«░Я»ѕ Я««Я»ЄЯ«▓Я»єЯ«┤Я»ЂЯ««Я»ЇЯ«фЯ«┐ Я«ЋЯ«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ«ЪЯ«ЕЯ»Ї Я«џЯ»ЄЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ Я«цЯ»ѓЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«јЯ«▒Я«┐Я«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
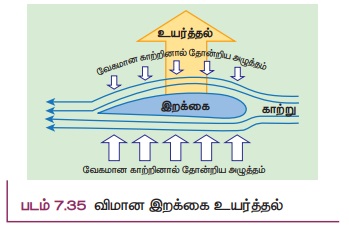
(Я«є) Я«хЯ«┐Я««Я«ЙЯ«Е Я«ЄЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ѕ Я«ЅЯ«»Я«░Я»ЇЯ«цЯ»ЇЯ«цЯ«▓Я»Ї (Aerofol lift)
Я«хЯ«ЙЯ«ЕЯ»ѓЯ«░Я»ЇЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЄЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«ЋЯ«│Я«ЙЯ«ЕЯ«цЯ»Ђ, Я««Я»ЄЯ«▓Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐ Я«ЋЯ»ђЯ«┤Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я»ѕ Я«хЯ«┐Я«Ъ Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«Ћ Я«хЯ«│Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ««Я»Ї, Я««Я»ЂЯ«ЕЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«ЕЯ»ѕ Я«фЯ«┐Я«ЕЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐ Я««Я»ЂЯ«ЕЯ»ѕЯ«»Я»ѕЯ«хЯ«┐Я«Ъ Я«ЁЯ«ЋЯ«▓Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«хЯ«ЪЯ«┐Я«хЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»Ї Я«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е. Я«хЯ«ЙЯ«ЕЯ»ѓЯ«░Я»ЇЯ«цЯ«┐ Я«ЄЯ«»Я«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«ЄЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«ЋЯ»ђЯ«┤Я»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ«ЙЯ«▒Я»ЇЯ«▒Я»ѕЯ«хЯ«┐Я«Ъ Я«ЄЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я««Я»ЄЯ«▓Я»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ«ЙЯ«▒Я»ЇЯ«▒Я»Ђ Я«фЯ«ЪЯ««Я»Ї 7.35 Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«хЯ»ЄЯ«ЋЯ««Я«ЙЯ«Ћ Я«еЯ«ЋЯ«░Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ«цЯ»ЇЯ«цЯ»ЂЯ«хЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«ЄЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«ЋЯ»ђЯ«┤Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ, Я««Я»ЄЯ«▓Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я»ѕЯ«хЯ«┐Я«Ъ Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї Я«џЯ«ЋЯ»ЇЯ«цЯ«┐ Я«хЯ«ЙЯ«»Я»ЇЯ«еЯ»ЇЯ«ц Я«ЅЯ«»Я«░Я»ЇЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ЄЯ«▓Я»ЇЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«ЅЯ«еЯ»ЇЯ«цЯ»ЂЯ«хЯ«┐Я«џЯ»ѕ Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЁЯ«цЯ»Ђ Я«хЯ«ЙЯ«ЕЯ»ѓЯ«░Я»ЇЯ«цЯ«┐Я«»Я»ѕ Я««Я»ЄЯ«▓Я»ЇЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЅЯ«»Я«░Я«џЯ»Ї Я«џЯ»єЯ«»Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
(Я«Є) Я«фЯ»ЂЯ«ЕЯ»ЇЯ«џЯ«ЕЯ»Ї Я«џЯ»ЂЯ«ЪЯ«░Я«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ
Я«фЯ»ЂЯ«ЕЯ»ЇЯ«џЯ«ЕЯ»Ї Я«џЯ»ЂЯ«ЪЯ«░Я«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«јЯ«░Я«┐Я«хЯ«ЙЯ«»Я»Ђ Я«еЯ»ЂЯ«БЯ»ЇЯ«цЯ»ЂЯ«│Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я«ЙЯ«Ћ Я«ЁЯ«цЯ«┐Я«Ћ Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«хЯ»єЯ«│Я«┐Я«хЯ«░Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є Я«хЯ»єЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«▒Я»ЇЯ«▒Я«ЙЯ«ЕЯ«цЯ»Ђ Я«хЯ»ЄЯ«ЋЯ««Я«ЙЯ«Ћ Я«ЁЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ЂЯ«│Я»Ї Я«ЋЯ«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ«цЯ»Ї Я«цЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я»Є Я«еЯ»ЂЯ«┤Я»ѕЯ«еЯ»ЇЯ«цЯ»Ђ Я«јЯ«░Я«┐Я«хЯ«ЙЯ«»Я»ЂЯ«хЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«ЋЯ«▓Я«еЯ»ЇЯ«цЯ»Ђ Я«фЯ«ЪЯ««Я»Ї 7.36 Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«еЯ»ђЯ«▓ Я«еЯ«┐Я«▒Я«џЯ»Ї Я«џЯ»ЂЯ«ЪЯ«░Я»ѕЯ«цЯ»Ї Я«цЯ«░Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
(Я«ѕ) Я«хЯ»єЯ«ЕЯ»ЇЯ«џЯ»ЂЯ«░Я«┐Я««Я«ЙЯ«ЕЯ«┐ (Venturimeter)
Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ«░Я»ЂЯ«хЯ«┐Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ, Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я«┐Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«ЁЯ««Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я«ЙЯ«ц Я«еЯ»ђЯ«░Я»ЇЯ««Я««Я»Ї Я«фЯ«ЙЯ«»Я»ЂЯ««Я»Ї Я«хЯ»ђЯ«цЯ«цЯ»ЇЯ«цЯ»ѕ Я«фЯ«ЙЯ«»Я»ЂЯ««Я»Ї Я«хЯ»ЄЯ«ЋЯ««Я»Ї) Я«ЁЯ«│Я«хЯ«┐Я«Ъ Я«ЅЯ«цЯ«хЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«цЯ»Ђ Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«цЯ»Ђ A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї AРђЎ Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«░Я»Ђ Я«ЁЯ«ЋЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ (Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ A). Я«ЁЯ«хЯ»ѕ B Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ«▓Я«ЙЯ«Е (Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ a) Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е. U Я«хЯ«ЪЯ«┐Я«х Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ««Я«ЙЯ«ЕЯ«┐Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я«ЁЯ«ЋЯ«ЕЯ»ЇЯ«▒ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ«▓Я«ЙЯ«Е Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«»Я»Є Я«фЯ«ЪЯ««Я»Ї 7.37 Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ««Я«ЙЯ«ЕЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ«┐Я«░Я«хЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐ Рђў¤ЂmРђЎ
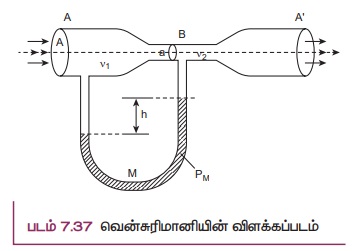
A Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«ЋЯ«▓Я««Я«ЙЯ«Е Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«фЯ«ЙЯ«»Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ««Я»Ї P1 Я«јЯ«ЕЯ»ЇЯ«Ћ. Рђў¤ЂРђЎ Я«ЁЯ«ЪЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«»Я»ЂЯ«ЪЯ«ЕЯ»Ї Рђўv1РђЎ Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ«ЙЯ«»Я»ЇЯ««Я««Я»Ї Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я«┐Я«ЕЯ»ЂЯ«│Я»ЇЯ«│Я»Є Я«фЯ«ЙЯ«»Я»ЇЯ«хЯ«цЯ«ЙЯ«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ«▓Я«ЙЯ«Е Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«хЯ»ЄЯ«ЋЯ««Я»Ї Рђўv2РђЎ Я«јЯ«Е Я«ЁЯ«цЯ«┐Я«ЋЯ«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«Ћ. Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«ЄЯ«еЯ»ЇЯ«ц Я«хЯ»ЄЯ«Ћ Я«ЁЯ«цЯ«┐Я«ЋЯ«░Я«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«ЕЯ«цЯ»Ђ B Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ«┐Я«» Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«фЯ«ЙЯ«»Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ««Я«ЙЯ«Е P2 Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є A Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї, B Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«хЯ»ЄЯ«▒Я»ЂЯ«фЯ«ЙЯ«ЪЯ«ЙЯ«ЕЯ«цЯ»Ђ (╬ћP = P1РѕњP2) Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ««Я«ЙЯ«ЕЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ«┐Я«░Я«хЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░ Я«хЯ»ЄЯ«▒Я»ЂЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї Я«ЁЯ«│Я«хЯ«┐Я«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐
Av1 = a v2
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ
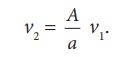
Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц
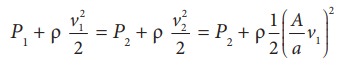
Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«БЯ»ЇЯ«Ъ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«ц Я«хЯ»ЄЯ«▒Я»ЂЯ«фЯ«ЙЯ«ЪЯ«ЙЯ«ЕЯ«цЯ»Ђ
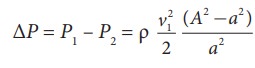
Я«јЯ«ЕЯ«хЯ»Є Я«ЁЯ«ЋЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я«┐Я«ЕЯ»Ї A Я««Я»ЂЯ«ЕЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«цЯ«┐Я«░Я«х Я«ЊЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«хЯ»ЄЯ«ЋЯ««Я»Ї
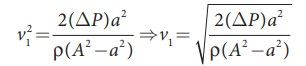
Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЕЯ«ЙЯ«ЪЯ«┐Я«»Я«┐Я«▓Я»Ї AЯ«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«ЙЯ«»Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«цЯ«┐Я«░Я«хЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«░Я»ЂЯ««Я«ЕЯ»Ї,
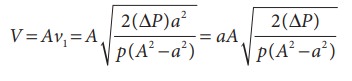
(Я«Ѕ) Я«фЯ«┐Я«▒Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
Я«фЯ»єЯ«░Я»ЇЯ«ЕЯ»єЯ«│Я«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я«ЙЯ«ЕЯ«цЯ»Ђ, Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я««Я«ЙЯ«Ћ Я«цЯ«ЙЯ«ЕЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«┐ Я«хЯ«ЙЯ«ЋЯ«ЕЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«░Я»ЄЯ«ЪЯ»ЇЯ«ЪЯ«░Я»Ї, Я«хЯ«ЪЯ«┐Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«┐ Я«фЯ««Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї, Я«цЯ»єЯ«│Я«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«хЯ«ЪЯ«┐Я«хЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЅЯ«цЯ«ЙЯ«░Я«БЯ««Я«ЙЯ«Ћ Я«ЋЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«░Я»ЄЯ«ЪЯ»ЇЯ«ЪЯ«░Я«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я»ЇЯ««Я»ЂЯ«ЕЯ»ѕ (nozzle) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«еЯ»ЂЯ«БЯ»ЇЯ«БЯ«┐Я«» Я«цЯ»ЂЯ«│Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я«ЙЯ«Ћ Я«ЋЯ«ЙЯ«▒Я»ЇЯ«▒Я«ЙЯ«ЕЯ«цЯ»Ђ Я««Я«┐Я«Ћ Я«хЯ»ЄЯ«ЋЯ««Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я»Є Я«хЯ«░Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«еЯ»ЇЯ«еЯ»ЄЯ«░Я»ЇЯ«хЯ«┐Я«▓Я»Ї Я«еЯ»ЂЯ«БЯ»ЇЯ«БЯ«┐Я«» Я«ЋЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЁЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, Я«фЯ»єЯ«ЪЯ»ЇЯ«░Я»ІЯ«▓Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«јЯ«░Я«┐Я«фЯ»іЯ«░Я»ЂЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«┐Я«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«хЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«ЋЯ«▓Я«ЕЯ«┐Я«▓Я»Ї Я«фЯ«▒Я»ЇЯ«▒Я«хЯ»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ«░Я«┐Я«»Я«ЙЯ«Е Я«ЁЯ«│Я«хЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«░Я«┐Я«фЯ»іЯ«░Я»ЂЯ«│Я»ЂЯ««Я»Ї Я«ЋЯ«▓Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
Я«њЯ«░Я»Ђ Я«џЯ«ЙЯ«ЪЯ«┐Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«цЯ»єЯ«░Я»ЇЯ««Я»ІЯ«ЋЯ»ІЯ«▓Я»Ї Я«фЯ«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«њЯ«░Я»Ђ Я«хЯ«│Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«┐Я«» Я«ЋЯ»ЂЯ«┤Я«ЙЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«џЯ«ЙЯ«ЪЯ«┐Я«»Я«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«фЯ«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»ЂЯ«│Я»Ї Я««Я»ѓЯ«┤Я»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«цЯ«┐Я«▒Я«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«хЯ»єЯ«│Я«┐ Я««Я»ЂЯ«ЕЯ»ѕЯ«»Я»ѕ Я«џЯ»ЂЯ«┤Я«▒Я»ЇЯ«▒Я«┐Я«ЕЯ«ЙЯ«▓Я»Ї, Я«цЯ»єЯ«░Я»ЇЯ««Я»ІЯ«ЋЯ»ІЯ«▓Я»Ї Я«фЯ«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я»Ї Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»ЂЯ««Я»Ї Я«цЯ»єЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«хЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«цЯ»ЂЯ«хЯ»Є Я«њЯ«░Я»Ђ Я«цЯ»єЯ«│Я«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«ЕЯ«┐Я«ЕЯ»Ї Я«цЯ«цЯ»ЇЯ«цЯ»ЂЯ«хЯ««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЅЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»єЯ«░Я«┐Я«»Я»ЂЯ««Я«Й?
Я«њЯ«░Я»Ђ Я«џЯ«┐Я«▓Я«еЯ»ЇЯ«цЯ«┐ Я«хЯ«▓Я»ѕ Я«еЯ«ЙЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ«хЯ«цЯ»ѕ Я«хЯ«┐Я«Ъ Я««Я«┐Я«ЋЯ«хЯ»ЂЯ««Я»Ї Я«хЯ«▓Я»ЂЯ«хЯ«ЙЯ«ЕЯ«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«џЯ«┐Я«▓Я«еЯ»ЇЯ«цЯ«┐ Я«хЯ«▓Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«цЯ«ЕЯ«┐ Я«еЯ»ѓЯ«▓Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЁЯ«цЯ«ЕЯ»Ї Я«еЯ«┐Я«▒Я»ѕЯ«»Я»ѕЯ«хЯ«┐Я«Ъ Я«фЯ«▓ Я«єЯ«»Я«┐Я«░Я««Я»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«еЯ«┐Я«▒Я»ѕ Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«фЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї. Я«џЯ«┐Я«▓Я«еЯ»ЇЯ«цЯ«┐ Я«хЯ«▓Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«»Я«ЎЯ»ЇЯ«ЋЯ»ЂЯ«БЯ«ЋЯ««Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Ћ 4.5├Ќ109Nm-2. Я«ЄЯ«еЯ»ЇЯ«ц Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕ Я««Я«░Я«ЋЯ»ЇЯ«ЋЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«»Я«ЎЯ»Ї Я«ЋЯ»ЂЯ«БЯ«Ћ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«њЯ«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«Ћ.
