Я«цЯ«ЕЯ«┐Я«еЯ«┐Я«▓Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї | Я«ЋЯ«БЯ«┐Я«цЯ«хЯ«┐Я«»Я«▓Я»Ї - Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«»Я«▓Я»ЇЯ«ЋЯ«│Я»Ї : Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я«јЯ«БЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї (Modular Arithmetic) | 12th Maths : UNIT 12 : Discrete Mathematics
12 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї : Я«ЁЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«»Я««Я»Ї 12 : Я«цЯ«ЕЯ«┐Я«еЯ«┐Я«▓Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї
Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«»Я«▓Я»ЇЯ«ЋЯ«│Я»Ї : Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я«јЯ«БЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї (Modular Arithmetic)
Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я«јЯ«БЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї (Modular Arithmetic)
Я«ЄЯ«цЯ»ЂЯ«хЯ«░Я»ѕ Я«хЯ«┤Я«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«Е Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«ц Я«џЯ»єЯ«»Я«▓Я«┐Я«ЋЯ«│Я»Ї, Я«ЁЯ«БЯ«┐Я«ЋЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї, Я«ЁЯ«БЯ«┐Я«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї, Я«фЯ»ѓЯ«▓Я«┐Я«»Я«ЕЯ»Ї Я«ЁЯ«БЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЄЯ«БЯ»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«єЯ«ЋЯ«┐Я«» Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«»Я«▓Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«хЯ«┐Я«хЯ«ЙЯ«цЯ«┐Я«цЯ»ЇЯ«цЯ»ІЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»Ї 'Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я«јЯ«БЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї' Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«цЯ«┐Я«» Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«»Я«▓Я«┐ Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«хЯ«┐Я«хЯ«ЙЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї. n > 1 Я«њЯ«░Я»ЂЯ««Я«┐Я«ЋЯ»ѕ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ n Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я«јЯ«БЯ»Ї' Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
a, b Я«єЯ«ЋЯ«┐Я«» Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я»ЂЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я»Ї n -Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ n -Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї a -Я««Я»Ї b - Я««Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«џЯ»ѕЯ«хЯ»Ђ Я«ЅЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»ѕЯ«»Я»Є Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ѓЯ«▓Я««Я»Ї, a = b(modn) Я«јЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«хЯ«░Я»Ї.
Я«ЄЯ«цЯ«ЕЯ»ЇЯ«фЯ«ЪЯ«┐ a - b = n k, k Рѕѕ Рёц Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a - Я«љ n Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ђЯ«цЯ«┐ b Я«єЯ«ЕЯ«цЯ»Ђ Я««Я«┐Я«ЋЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«еЯ»ЇЯ«ц Я««Я«┐Я«ЋЯ»ѕ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, 25 РЅА 4(mod7),-20 РЅА -2(mod3) РЅА 1(mod3) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 15 РЅА 0(mod5),... Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я««Я»ЂЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ»ѕ n Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ђЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«џЯ«ЙЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«ЋЯ»Ї Я«ЋЯ»ѓЯ«▒Я»ЂЯ«ЋЯ«│Я»Ї 0,1,2,...,n - 1 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Рёц5Я«▓Я»Ї
[0] = { .. ., Рѕњ15, Рѕњ10, Рѕњ5, 0, 5,10,15, Рђд }
[1] = {Рђд , Рѕњ14, Рѕњ9, Рѕњ4,1, 6, 11, Рђд}
[2] = {Рђд , Рѕњ13, Рѕњ8, Рѕњ3, 2, 7,12,Рђд]
[3] = {Рђд, Рѕњ12, Рѕњ7, Рѕњ2, 3,8,13,Рђд}
[4] = {Рђд , Рѕњ11, Рѕњ6, Рѕњ1, 4, 9,14,Рђд}.
Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ
Рёц5 = {[0],[1],[ 2],[3],[ 4]} . Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»ЂЯ««Я»Ї Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ 5Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«џЯ»ѕЯ«хЯ»Ђ Я«ЅЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЋЯ»ЂЯ«▒Я»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Рёц5 Я«»Я»ѕ Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«Ћ Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЅЯ«фЯ«»Я»ІЯ«ЋЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
2007Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЕЯ»Ї, Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ 10-Я«ЄЯ«▓Я«ЋЯ»ЇЯ«Ћ ISBN (Я«џЯ«░Я»ЇЯ«хЯ«цЯ»ЄЯ«џ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Е Я«цЯ«░ Я«фЯ»ЂЯ«цЯ»ЇЯ«цЯ«Ћ Я«јЯ«БЯ»Ї/International Standard Book Number) Я«јЯ«БЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ. Я«ЅЯ«цЯ«ЙЯ«░Я«БЯ««Я«ЙЯ«Ћ, Я«ЋЯ«ЪЯ»ѕЯ«џЯ«┐ Я«ЄЯ«▓Я«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ Я«џЯ««Я«еЯ«┐Я«▓Я»ѕ Я«џЯ»ІЯ«цЯ«ЕЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ {0,1,2,3,4,5,6,7,8,9,X} Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. 81-7808-755-3 Я«јЯ«ЕЯ»ЇЯ«▒ ISBN Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«▓Я»Ї Я«ЋЯ«ЪЯ»ѕЯ«џЯ«┐ Я«ЄЯ«▓Я«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«Е 3 Я«єЯ«ЕЯ«цЯ»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ»єЯ«▒Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
1*8+2*1+3*7+ 4*8+5*0+6*8 + 7*7+8*5+9*5 = 8+2+21+32 +0+48+49 +40+45 = 245 РЅА 3 (Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ 11).
Я««Я«ЙЯ«▒Я»ЇЯ«▒Я«ЙЯ«Ћ Я«еЯ«┐Я«▒Я»ѕЯ«»Я«┐Я«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«фЯ«┐Я«ЕЯ»Ї Я«цЯ«┐Я«░Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ѕ Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
9*8+8*1+7*7+6*8 +5*0+4*8+3*7+2*5+1*5 = 245 = 3 (Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ 11).
Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«┤Я«┐Я«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї, Я«еЯ«ЙЯ««Я»Ї Я«њЯ«░Я»Є Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ»Ђ (check) Я«јЯ«БЯ»Ї 3 Я«љЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЂЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
2007-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ«┐Я«▒Я«ЋЯ»Ђ 13- Я«ЄЯ«▓Я«ЋЯ»ЇЯ«Ћ ISBN Я«јЯ«БЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«фЯ«▒Я»ЇЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. (Я«ЄЯ«ЪЯ««Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«хЯ«▓Я««Я«ЙЯ«Ћ) Я«хЯ«▓Я««Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЄЯ«ЪЯ««Я«ЙЯ«ЋЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї 12 Я«ЄЯ«▓Я«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ 3, 1, 3, 1,. Я«јЯ«ЕЯ»ЇЯ«ЋЯ«┐Я«▒ Я«еЯ«┐Я«▒Я»ѕЯ«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«░Я»Ї Я«еЯ«┐Я«▒Я»ѕЯ«»Я«┐Я«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. 10 -Я«ЕЯ»Ї Я«ЁЯ«цЯ«┐Я«Ћ Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«░Я»Ї Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ 10 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ«цЯ«┐Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«ЄЯ«▓Я«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЅЯ«цЯ«ЙЯ«░Я«БЯ««Я«ЙЯ«Ћ, 978-81-931995-6-5 Я«јЯ«ЕЯ»ЇЯ«▒ ISBN Я«јЯ«БЯ»ЇЯ«БЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї. Я«ЄЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«ЪЯ««Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«хЯ«▓Я««Я«ЙЯ«Ћ 12 Я«ЄЯ«▓Я«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї.

Я«ЄЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«▒Я»ЂЯ«цЯ«┐ Я«еЯ«┐Я«░Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 155 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. 10 -Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЁЯ«░Я»ЂЯ«ЋЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ (Я«ЅЯ«»Я«░Я»Ї) Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї 160 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. 160-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 155-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я»Ї 5 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є 5-Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ 10 - Я«љ Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»Ђ 5 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ ISBN Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«▓Я»Ї 13-Я«хЯ«цЯ»Ђ Я«ЄЯ«▓Я«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї, n Я«љ Я«хЯ«┐Я«Ъ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«хЯ«ЙЯ«Е Я««Я«┐Я«ЋЯ»ѕ Я««Я»ЂЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЋЯ«БЯ««Я»Ї Рёцn -Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ "n-Я«ЕЯ»Ї Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї n( +n ) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї "n-Я«ЕЯ»Ї Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї n(├Ќn ) Я«єЯ«ЋЯ«┐Я«» Я«фЯ»ЂЯ«цЯ«┐Я«» Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«џЯ»єЯ«»Я«▓Я«┐Я«ЋЯ«│Я»ѕ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ 12.6
(i) n -Я«ЕЯ»Ї Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я«ЙЯ«ЕЯ«цЯ»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. - a,b Рѕѕ Рёцn Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«фЯ«┐Я«▒Я«ЋЯ»Ђ a + b Я«љ n Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«Ћ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ђЯ«цЯ«┐ a + nb
(ii) n -Я«ЕЯ»Ї Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ«ЕЯ«цЯ»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
a,b Рѕѕ Рёцn., Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«фЯ«┐Я«▒Я«ЋЯ»Ђ a ├Ќ b Я«љ n Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«Ћ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ђЯ«цЯ«┐ a + nb
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 12.9
Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї 5 Я«џЯ»єЯ«»Я«▓Я«┐ Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«ЋЯ«БЯ««Я»Ї Рёц5 -Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ +5 Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ»єЯ«»Я«▓Я«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ (i) Я«ЁЯ«ЪЯ»ѕЯ«хЯ»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ (ii) Я«фЯ«░Я«┐Я««Я«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ (iii) Я«џЯ»ЄЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ (iv) Я«џЯ««Я«ЕЯ«┐Я«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (v) Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕЯ«ЋЯ«│Я»ѕЯ«џЯ»Ї Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Рёц5 = {[ 0 ], [1], [2], [3], [4]} Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ 5 Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї Я«џЯ»єЯ«»Я«▓Я«┐ Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕ Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«фЯ»єЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я««Я»ђЯ«цЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ {0,1,2,3,4} {[0],[1],[2],[3],[4]} Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
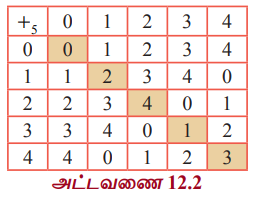
(i) Я«џЯ»єЯ«»Я«▓Я«┐ Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Рёц5.-Я«ЕЯ»Ї Я«џЯ«░Я«┐Я«»Я«ЙЯ«Ћ Я«ЊЯ«░Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ѓЯ«▓Я««Я»ЇЯ«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї a+5 b -Я«ЕЯ»Ї Я«хЯ«┐Я«│Я»ѕЯ«хЯ»Ђ Я«њЯ«░Я»ЂЯ««Я»ѕЯ«цЯ»ЇЯ«цЯ«ЕЯ»ЇЯ««Я»ѕ Я«хЯ«ЙЯ«»Я»ЇЯ«еЯ»ЇЯ«цЯ«цЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є, +5 Я«єЯ«ЕЯ«цЯ»Ђ Рёц5-Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ѕЯ«хЯ»Ђ Я«фЯ»єЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
(ii) Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«фЯ«цЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«цЯ«ЕЯ»ЇЯ««Я»ѕ Я««Я»ѓЯ«▓Я»ѕЯ«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«џЯ««Я«џЯ»ЇЯ«џЯ»ђЯ«░Я«ЙЯ«Ћ Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ«ЙЯ«▓Я»Ї +5 Я«єЯ«ЕЯ«цЯ»Ђ Я«фЯ«░Я«┐Я««Я«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ»Ђ.
(iii) Я«џЯ»ЄЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ѕ Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«»Я«▓Я«┐ Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«»Я»ѕ Я«еЯ»ЄЯ«░Я«ЪЯ«┐Я«»Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ««Я»ЂЯ«ЪЯ«┐Я«»Я«ЙЯ«цЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«цЯ»ѕ Я«хЯ«┤Я«ЋЯ»ЇЯ«ЋЯ««Я»ЇЯ«фЯ»ІЯ«▓ Я«ЊЯ«░Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
2,3,4 Рѕѕ Рёц5, Я«јЯ«ЕЯ«┐Я«▓Я»Ї, (2+5, 3) +5 4 = 0+5 4 = 4 (Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ 5)
2+5 (3+5 4) = 2+5 2 = 4 (Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ 5)
Я«јЯ«ЕЯ«хЯ»Є, (2+5 3) +5 4 = 2+5 (3+5 4).
Я«ЄЯ«цЯ»Ђ Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«џЯ«ЙЯ«цЯ»ЇЯ«цЯ«┐Я«»Я««Я«ЙЯ«Е Я««Я»ЂЯ««Я»ЇЯ««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«цЯ»ѕ Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ Я««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я»Ї. Я««Я»ЂЯ«ЪЯ«┐Я«хЯ«ЙЯ«Ћ, +5 Я«єЯ«ЕЯ«цЯ»Ђ Я«џЯ»ЄЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ѕ Я«еЯ«┐Я«▒Я»ѕЯ«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї Я«јЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«▓Я«ЙЯ««Я»Ї.
(iv) 0 Я«цЯ«▓Я»ѕЯ««Я»ѕЯ«»Я«┐Я«▓Я«ЙЯ«Е Я«еЯ«┐Я«░Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я«▓Я»Ї Я«њЯ«░Я»Є Я««Я«ЙЯ«цЯ«┐Я«░Я«┐Я«»Я«ЙЯ«ЕЯ«хЯ»ѕ. Я«јЯ«ЕЯ«хЯ»Є, 0 Рѕѕ Рёц5 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«џЯ««Я«ЕЯ«┐ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
(v) Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«еЯ«┐Я«░Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я«▓Я«┐Я«▓Я»ЂЯ««Я»Ї Я«џЯ««Я«ЕЯ«┐ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ 0 Я«ЅЯ«│Я»ЇЯ«│Я«цЯ«ЙЯ«▓Я»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«цЯ«┐Я«џЯ»єЯ«»Я»ЇЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є, Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕ 12.2-Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ Я«ЅЯ«БЯ»ЇЯ««Я»ѕ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»єЯ«│Я«┐Я«хЯ«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ
Рђб Рёц5 -Я«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«ЊЯ«░Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Рђў2' Я«ЄЯ«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я«ЋЯ»ђЯ«┤Я»Є Я«ЋЯ»ІЯ«ЪЯ«┐Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
Рђб 2 Я«цЯ«▓Я»ѕЯ««Я»ѕЯ«»Я«┐Я«▓Я«ЙЯ«Е III Я«хЯ«цЯ»Ђ Я«еЯ«┐Я«░Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«џЯ««Я«ЕЯ«┐ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«еЯ«┐Я«▓Я»ѕЯ«»Я»ѕ Я««Я»ЂЯ«цЯ«▓Я«┐Я«▓Я»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«»Я«хЯ»ЂЯ««Я»Ї. III Я«хЯ«цЯ»Ђ Я«еЯ«┐Я«░Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ««Я«ЪЯ»ЇЯ«ЪЯ««Я«ЙЯ«Ћ Я«еЯ«ЋЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ 0 Я«љ Я«ЁЯ«ЪЯ»ѕЯ«еЯ»ЇЯ«ц Я«фЯ«┐Я«▒Я«ЋЯ»Ђ IV Я«хЯ«цЯ»Ђ Я«еЯ«┐Я«░Я«▓Я«┐Я«▓Я»Ї 0 - Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»Є Я«еЯ«ЋЯ«░Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 3-Я«љЯ«цЯ«ЙЯ«ЕЯ»Ї 2-Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«хЯ«░Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЄЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«ЁЯ«цЯ»ЇЯ«цЯ«ЙЯ«ЪЯ»ЇЯ«џЯ«┐Я«»Я«ЙЯ«Ћ 2+3 = 0 (Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ 5) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ЂЯ««Я»Ї Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«ЙЯ«хЯ«цЯ«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї. Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї, 0 Я«єЯ«ЕЯ«цЯ»Ђ III Я«хЯ«цЯ»Ђ Я«еЯ«┐Я«░Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї IVЯ«хЯ«цЯ»Ђ Я«еЯ«┐Я«░Я«▓Я»ѕ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. IV Я«хЯ«цЯ»Ђ Я«еЯ«┐Я«░Я«▓Я«┐Я«▓Я»Ї Я««Я«┐Я«Ћ Я«ЅЯ«»Я«░Я»ЇЯ«еЯ»ЇЯ«ц Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ»єЯ«▒Я»ЇЯ«▒ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ 3 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є 2-Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ 3 Я«љЯ«цЯ»Ї Я«цЯ«хЯ«┐Я«░ Я«хЯ»ЄЯ«▒Я«┐Я«▓Я»ЇЯ«▓Я»ѕ. Я«ЄЯ«цЯ»ЄЯ«хЯ«┤Я«┐Я«»Я«┐Я«▓Я»Ї Рёц5 -Я«ЕЯ»Ї Я«њЯ«хЯ»ЇЯ«хЯ»ІЯ«░Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Рђб Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я«ЙЯ«Ћ 0-Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ 0 Рѕѕ Рёц5 1 -Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ 4 Рѕѕ Рёц5 2-Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ 3 Рѕѕ Рёц5 3-Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ 2 Рѕѕ Рёц5, 4 -Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ 1 Рѕѕ Рёц5 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 12.10
Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ 11Я«љЯ«фЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«јЯ«џЯ»ЇЯ«џЯ«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ««Я»Ї {0,1,2,3,4,5,6,7,8,9,10} -Я«ЄЯ«ЕЯ»Ї Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ«БЯ««Я»Ї A = {1,3,4,5,9} -Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ ├Ќ11 Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ»єЯ«»Я«▓Я«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ (i) Я«ЁЯ«ЪЯ»ѕЯ«хЯ»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ (ii) Я«фЯ«░Я«┐Я««Я«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ (iii) Я«џЯ»ЄЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ (iv) Я«џЯ««Я«ЕЯ«┐Я«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ (V) Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕЯ«ЋЯ«│Я»ѕЯ«џЯ»Ї Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
├Ќ11 Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ»єЯ«»Я«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«џЯ»єЯ«»Я«▓Я«┐ Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕ Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ.
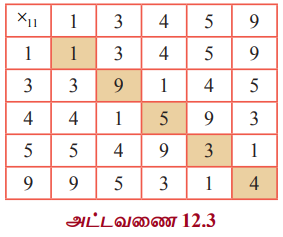
Я««Я»ЂЯ«еЯ»ЇЯ«цЯ»ѕЯ«» Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«хЯ«┐Я«хЯ«░Я«┐Я«цЯ»ЇЯ«цЯ«фЯ«ЪЯ«┐ ├Ќ11 Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ»єЯ«»Я«▓Я«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ A-Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«џЯ»Ї Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«БЯ»ЇЯ«ЪЯ«хЯ«ЙЯ«▒Я»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
(i) Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї A-Я«▓Я»Ї Я«џЯ«░Я«┐Я«»Я«ЙЯ«Ћ Я«ЊЯ«░Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ѓЯ«▓Я««Я»ЇЯ«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї ├Ќ11, A -Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ѕЯ«хЯ»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ Я«фЯ»єЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
(ii) Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«цЯ«ЕЯ»ЇЯ««Я»ѕ Я««Я»ѓЯ«▓Я»ѕЯ«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«џЯ««Я«џЯ»ЇЯ«џЯ»ђЯ«░Я«ЙЯ«ЋЯ«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї, ├Ќ11 Я«фЯ«░Я«┐Я««Я«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
(iii) ├Ќ11 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«хЯ«┤Я«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«Ћ Я«џЯ»ЄЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
(iv) 1 Я«цЯ«▓Я»ѕЯ««Я»ѕЯ«»Я«┐Я«▓Я«ЙЯ«Е Я«еЯ«┐Я«░Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я«▓Я»Ї Я«њЯ«░Я»Є Я««Я«ЙЯ«цЯ«┐Я«░Я«┐Я«»Я«ЙЯ«ЕЯ«хЯ»ѕ. Я«јЯ«ЕЯ«хЯ»Є, 1 Рѕѕ A Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«џЯ««Я«ЕЯ«┐ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
(v) Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«еЯ«┐Я«░Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я«▓Я«┐Я«▓Я»Ї Я«џЯ««Я«ЕЯ«┐ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ 1 Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ ├Ќ11-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. 1 -Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ 1Рѕѕ A, 3 -Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ 4 Рѕѕ A , 4-Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ 3Рѕѕ A, 5 -Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ 9 Рѕѕ A, 9-Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ««Я«▒Я»ѕ 5 Рѕѕ A Я«єЯ«ЋЯ»ЂЯ««Я»Ї.