தனிநிலைக் கணிதம் | கணிதவியல் - ஈருறுப்புச் செயலிகள் (Binary Operations) வரையறைகள் (Definitions) | 12th Maths : UNIT 12 : Discrete Mathematics
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 12 : தனிநிலைக் கணிதம்
ஈருறுப்புச் செயலிகள் (Binary Operations) வரையறைகள் (Definitions)
ஈருறுப்புச் செயலிகள் (Binary Operations)
வரையறைகள் (Definitions)
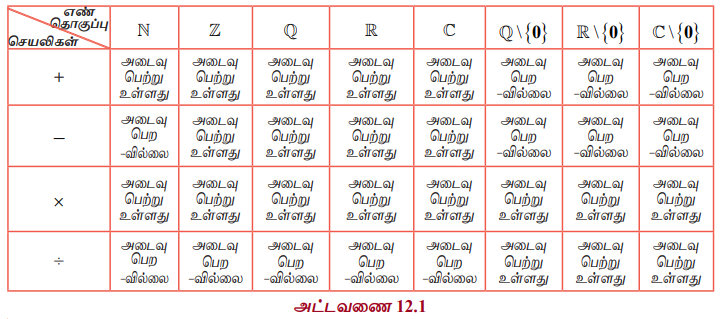
ℝ-ன் மீது அடிப்படை எண்கணித ஈருறுப்புச் செயலிகள் கூட்டல் (+), கழித்தல் (-), பெருக்கல் (×), மற்றும் வகுத்தல் (÷) என்பவைகளாகும். 19ஆம் நூற்றாண்டின் இறுதியிலும் மற்றும் 20ஆம் நூற்றாண்டின் தொடக்கத்திலும் வாழ்ந்த கணித அறிஞர்கள் எபேல், கெய்லி, கோஷி போன்றோர் மேற்கூறிய வழக்கமான இயற்கணிதச் செயலிகள் நிறைவு செய்யும் பண்புகளை பொதுமைப்படுத்த முயற்சி செய்தார்கள். அதன் மூலம் அவர்கள் புதிய நுண் இயற்கணித அமைப்புகளைக் கொள்கை ரீதியான அணு குமுறை மூலம் உருவாக்கினார்கள். அவ்வாறு பெறப்பட்ட இந்த புதிய பிரிவு நுண் இயற்கணிதம் என்று அழைக்கப்படுகின்றது.
எடுத்துக்காட்டாக ஏதேனும் இரு இயல் எண்களின் கூடுதல் ஓர் இயல் எண் என்றும் அவற்றின் பெருக்கலும் ஓர் இயல் எண் என்றும் அறிவோம். அதாவது, வழக்கமான கூட்டல் (+) மற்றும் (×) பெருக்கல் செயலிகள் ℕ என்ற கணத்தில் இரு உறுப்புகளைக் கொண்டு செயல்படுத்துவதால் ஈருறுப்புச் செயலி என்று அழைக்கப்படுகின்றன.
அதையே குறியீட்டு வடிவில், m + n ∈ ℕ ; m × n ∈ ℕ, ∀m, n ∈ ℕ = {1, 2, 3,...}என்று எழுதுகிறோம்.
மேற்கூறிய இரண்டு ஈருறுப்புச் செயல்களும் கீழ்க்காணும் விதிகளை நிறைவுச் செய்வதைக் கவனிக்க.
(1) ℕ-ல் இருந்து ஒரே நேரத்தில் இரண்டு எண்கள் எடுக்கப்பட்டு செயல்படுத்தப்படுகின்றன.
(2) அவைகளின் முடிவில் கிடைக்கும் உறுப்பு மீண்டும் ℕ என்ற கணத்திலேயே இருக்கிறது.இவ்வாறாக ஒரு வெற்றற்ற கணம் மீது வரையறுக்கப்படும் எந்த ஒரு செயலையும் நுண்கணிதத்தில் ஒரு ஈருறுப்பு செயலி அல்லது ஈருறுப்புத் தொகுப்பு எனப்படும்.
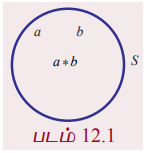
வரையறை 12.1
ஒரு வெற்றற்ற கணம் S-இன் மீது வரையறுக்கப்பட்ட * என்ற ஏதேனும் ஒரு செயல், ஓர் ஈருறுப்புச் செயல் என அழைக்கப்படவேண்டுமெனில் அது பின்வரும் பண்புகளைக் கொண்டிருக்க வேண்டும்.
(i) S × S -ல் உள்ள ஒவ்வொரு வரிசைச் சோடி (a,b)-க்கு * என்ற செயல் கண்டிப்பாக வரையறுக்கப்பட்டிருக்க வேண்டும்.
(ii) S × S -ல் ஒவ்வொரு வரிசைச் சோடி (a,b)-யுடன் S-ல் a* b என்ற ஒரே ஓர் உறுப்புஇருக்கும்.
வேறுவிதமாகச் கூறினால், S -ன் மீது வரையறுக்கப்படும் * என்ற ஈருறுப்புச் செயலானது S -ல் உள்ள உறுப்புகளின் ஒவ்வொரு வரிசைச் சோடியையும் S -ல் ஒரே ஓர் உறுப்பைத் தொடர்புபடுத்தும் ஒரு விதி ஆகும். இதனை ஒரு சார்பாகவும் பின்வருமாறு வரையறுக்கலாம்.
* S × S → S ; அதாவது, *(a, b) = a*b ∈ S, இங்கு a*b என்பது ஒரே ஓர் உறுப்பாகும்.
*-ன்விளைவு a * b எப்பொழுதும் கண்டிப்பாக S -ல் அமைய வேண்டும் மற்றும் S - க்கு வெளியே அமையக்கூடாது. இந்நிலையில் S-ஆனது *-ன் கீழ் அடைவு பெற்றுள்ளது எனக் கூறலாம். இப்பண்பை அடைவுப் பண்பு என்று கூறுவர்.
வரையறை 12.2
ஒன்று அல்லது அதற்கு மேற்பட்ட ஈருறுப்புச் செயல்களைப் பொருத்து ஏதேனும் ஒரு வெற்றற்ற கணத்தின் மீது வரையறுக்கப்பட்டால் அது இயற்கணித அமைப்பு எனப்படும்.
* என்ற ஈருறுப்புச் செயலை S-இன் மீது பின்வருமாறும் வரையறுக்கலாம்: ∀ a , b ∈ S , a* b என்பது ஒருமைத்தன்மை வாய்ந்தது, மேலும் a*b ∈ S.
குறிப்பு
மேலேயுள்ள வறையறையிலிருந்து ஒவ்வொரு ஈருறுப்புச் செயலும் அடைவுப் பண்பை நிறைவு செய்யும் என்பது தெளிவாகிறது.
குறிப்பு
* என்ற செயல் ஒரு குறியீடுதான். இது +, × , - , ÷ அணிக் கூட்டல், அணிப் பெருக்கல், அணிவகுத்தல் ஆகியவை ஈருறுப்புச் செயலியாக இருப்பதோ (அ) இல்லாமலிருப்பதோ அது வரையறுக்கப்படும் கணத்தைப் பொருத்ததாகும்.
எடுத்துக்காட்டாக, வழக்கமான கூட்டல் + மற்றும் பெருக்கல் × ஆனது ℕ -ன் மீது ஓர் ஈருறுப்புச் செயல் ஆகும். ஆனால், கழித்தல் - ஆனது ℕ -ன் மீது ஓர் ஈருறுப்புச் செயல் ஆகாது.
இதனை சரிபார்க்க. (3,4) ∈ ℕ × ℕ என்க.
∗ ( a , b) = − (3, 4) = 3 − 4 = −1 ∉ ℕ.
எனவே -ஆனது ℕ -ன் மீது ஓர் ஈருறுப்புச் செயல் ஆகாது. அதே சமயத்தில் - ஆனது ℤ -ன் மீது ஓர் ஈருறுப்புச் செயல் என்பது தெளிவு. எனவே, ℤ ஆனது +, × மற்றும் - ஐ பொருத்து கீழ் அடைவு பெற்றுள்ளது. எனவே, (ℤ , +, ×, -) ஓர் இயற்கணித அமைப்பு ஆகும்.
உற்றுநோக்கி அறிந்தவை
ஒரு செயலின் ஈருறுப்புப் பண்பானது அது வரையறுக்கப்படும் கணத்தைப் பொருத்ததாகும்.
(a) ℕ உடன் 0 மற்றும் குறை முழு எண்களையும் சேர்த்து விரிவுபடுத்தப்பட்ட கணம்தான் ℤ எனப்படும் முழு எண் கணம் ஆகும். ℤ -ன் மீது - ஆனது ஒரு ஈருறுப்புச் செயலி ஆகும். ஆனால் ℕ -ன் மீது - ஒரு ஈருறுப்புச் செயலி ஆகாது.
(b) செயலி ÷ ஆனது, ℤ -ன் மீது ஓர் ஈருறுப்புச் செயல் ஆகாது. எடுத்துக்காட்டாக, (1,2) ∈ ℤ × ℤ க்கு ÷ (1, 2) = 1/2 ∉ ℤ. எனவே, ℤ. என்ற கணத்தை விரிவுபடுத்தக் கிடைக்கப்பெறும கணம் ℚ ஆகும்.
(c) எண்களைக் கொண்ட அடிப்படைச் செயல்பாடுகளில் '0' ஆல் வகுப்பது
வரையறுக்கப்படவில்லை என்ற உண்மையை அறிவோம். எனவே, ÷ ஆனது ℚ \{0} -ன் மீது ஓர் ஈருறுப்புச் செயல் ஆகும். இவ்வாறே +, × , - ஆகியவைகள் Q -ன் மீது ஈருறுப்புச் செயல்கள் ஆகும் ஆனால் ÷ ஆனது ℚ \{0}-ன் மீது அமையும் ஓர் ஈருறுப்புச் செயல் ஆகும்.
மேற்கொண்டு ℚ ஐ ℝ -க்கும் மற்றும் ℝ ஐ C-க்கும் விரிவுபடுத்துவதற்குக் காரணம் என்ன? என்ற வினா எழுந்துள்ளது. எனவே, +, -, ×, ÷ ஆகிய அடிப்படையான எண்கணித செயல்களுடன் " x2 − 2 = 0 ” ; “ x2 + 1 = 0 ”. என்ற சமன்பாட்டு வகைகளின் மூலங்களையும் உள்ளடக்கிய ஒரு எண் தொகுப்பு தேவைப்படுகிறது. எனவே, ஏற்கனவே உள்ள எண் தொகுப்புடன் விகிதமுறா எண்களையும்திரட்டி (அத்தியாயம் 3ஐப் பார்க்க உள்ளடக்கும் பொழுது கிடைக்கும் எண் தொகுப்பானது ℝ -ம் C-ம் ஆகும். இதில் மிகப்பெரிய எண் தொகுப்பான C ஆனது முறையே ℕ, ℤ, ℚ மற்றும் ℝ ஆகிய எண் தொகுப்புகளை கொண்டிருக்கும் உட்கணங்களாக இருக்கும்.
எடுத்துக்காட்டு 12.1
கீழ்க்காணும் ஈருறுப்புச் செயலிகள், அதற்குரிய கணங்களில் அடைவுப் பண்பைப் பெற்றுள்ளதா என்பதைச் சோதிக்க. அவ்வாறில்லாதவற்றிற்கு ஈருப்புச் செயலியின் நிபந்தனையை நிறைவேற்றும் முறையைக் காண்க.
(i) a ∗ b = a + 3ab − 5b2 ; ∀ a,b ∈ ℤ
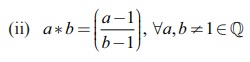
தீர்வு
(i) ℤ -இன் மீது × ஆனது ஈருறுப்புச் செயலி என்பதால் ∀ a , b ∈ ℤ ⇒ a × b = ab ∈ ℤ மற்றும் b × b = b2 ∈ ℤ ... (1)
ℤ -ன் மீது + ஆனது ஈருறுப்புச் செயலி என்பதால் (1) ⇒ 3ab = ( ab + ab + ab) ∈ ℤ மற்றும் 5b2 = (b2 + b2 + b2 + b2 + b2) ∈ ℤ. .... (2)
மேலும், a ∈ ℤ மற்றும் 3ab ∈ ℤ ⇒ a + 3ab ∈ ℤ. ... (3)
(2), (3) ஆகியவற்றிலிருந்து ℤ -ன் மீது ‘-‘ ஆனது ஈருறுப்புச் செயலி என்பதாலும் a*b = (a + 3ab – 5b2) ∈ ℤ கிடைக்கும். எனவே a* b ∈ ℤ என்பதால் * ஆனது ℤ -ன் மீதுஅடைவு பெற்றுள்ளது.
(ii) இந்த எடுத்துக்காட்டில், a*b ஆனது ஒரு பின்ன வடிவில் உள்ளது. 0 ஆல் வகுப்பது வரையறுக்கப்படாததால் கொடுக்கப்பட்ட பின்னத்தின் பகுதி b - 1 கண்டிப்பாக பூச்சியமற்றதாக இருக்க வேண்டும்.
b = 1 எனில், b - 1 = 0 என்பது உண்மை . 1 ∈ ℚ என்பதால் * ஆனது ℚ -ன் மீது அடைவு பெறவில்லை . எனவே ℚ -ல் இருந்து 1 ஐ நீக்க a* b -ன் விளைவு ℚ \{1}-ல் இருக்கும்.எனவே, * ஆனது ℚ \{1}-ன் மீது அடைவு பெற்றுள்ளது.