வரையறை, விளக்கம், தீர்க்கப்பட்ட எடுத்துக்காட்டு சிக்கல்கள் - பயட் - சாவர்ட் விதி | 12th Physics : UNIT 3 : Magnetism and Magnetic Effects of Electric Current
12 வது இயற்பியல் : அலகு 3 : காந்தவியல் மற்றும் மின்னோட்டத்தின் காந்தவிளைவுகள்
பயட் - சாவர்ட் விதி
பயட் - சாவர்ட் விதி (BIOT - SAVART LAW)
ஆர்ஸ்டெட்டின்கண்டுபிடிப்பைத் தொடர்ந்து, ஜீன்
- பாப்டிஸ்ட் பயட் மற்றும் பெலிக்ஸ் சாவர்ட் இருவரும் 1819 இல் மின்னோட்டம் பாயும்
கடத்திக்கு அருகே வைக்கப்பட்ட காந்தம் உணரும் விசையை அளந்தறியும் சோதனைகளை மேற்கொண்டு
கணிதவியல் சமன்பாட்டை உருவாக்கினார்கள்.
இச்சமன்பாடு வெளியில் ஒரு புள்ளியில் உருவாகும்
காந்தப்புலத்தை, அக்காந்தப்புலத்தை உருவாக்கும் மின்னோட்டத்தின் அடிப்படையில் கணக்கிடுகிறது.
இது எல்லா வித வடிவ அமைப்புள்ள கடத்திகளுக்கும் பொருந்தும்.
1. பயட் - சாவர்ட் விதியின் வரையறை மற்றும் விளக்கம்
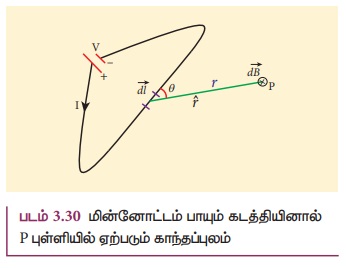
மின்னோட்டம் பாயும் கடத்தியின் நீளத்தின் சிறு
கூறிலிருந்து r தொலைவில் உள்ள P புள்ளியில் படம் 3.30 உருவாகும் காந்தப்புலம் ![]() இன் எண்மதிப்பை பயட் மற்றும் சாவர்ட் சோதனையின் அடிப்படையில் கண்டறிந்தனர். இதன் அடிப்படையில்
காந்தப்புலம்
இன் எண்மதிப்பை பயட் மற்றும் சாவர்ட் சோதனையின் அடிப்படையில் கண்டறிந்தனர். இதன் அடிப்படையில்
காந்தப்புலம் ![]() இன் எண்மதிப்பு
இன் எண்மதிப்பு
(i) மின்னோட்டத்தின் (I) வலிமைக்கு நேர்த்தகவிலும்
(ii) நீளக் கூறின் ![]() எண்மதிப்புக்கு
நேர்த்தகவிலும்
எண்மதிப்புக்கு
நேர்த்தகவிலும்
(iii) ![]() மற்றும் r^ க்கு இடையே உள்ள
கோணத்தின்θசைன் மதிப்புக்கு நேர்த்தகவிலும்
மற்றும் r^ க்கு இடையே உள்ள
கோணத்தின்θசைன் மதிப்புக்கு நேர்த்தகவிலும்
(iv) புள்ளி P மற்றும் நீளக்கூறு ![]() இவற்றுக்குஇடையே உள்ள தொலைவின் இருமடிக்கு எதிர்த்தகவிலும் இருக்கும்.
இவற்றுக்குஇடையே உள்ள தொலைவின் இருமடிக்கு எதிர்த்தகவிலும் இருக்கும்.
இதனை பின்வருமாறு எழுதலாம்


இங்கு k = μo/ 4π(SI அலகில்)
வெக்டர் குறியீட்டின்படி,
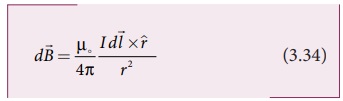
இங்கு ![]() வெக்டரானது, மின்னோட்டம் பாயும்
திசையைக் காட்டும் I
வெக்டரானது, மின்னோட்டம் பாயும்
திசையைக் காட்டும் I![]() மற்றும்
மற்றும் ![]() யில் இருந்து P புள்ளியை நோக்கிச் செயல்படும்
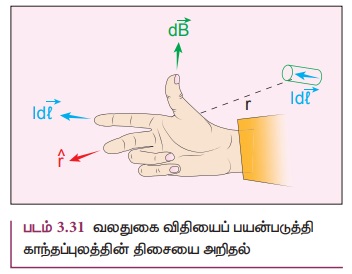
ஓரலகு வெக்டர் r^ ஆகிய இரண்டிற்கும் செங்குத்தாக இருக்கும் (படம் 3.31).
யில் இருந்து P புள்ளியை நோக்கிச் செயல்படும்
ஓரலகு வெக்டர் r^ ஆகிய இரண்டிற்கும் செங்குத்தாக இருக்கும் (படம் 3.31).
சமன்பாடு (3.34) ஐப் பயன்படுத்தி, கடத்தியின்
சிறு நீளக்கூறினால் ஏற்படும் காந்தப்புலத்தை மட்டுமே கணக்கிட இயலும். அனைத்து மின்னோட்டக்கூறுகளின் I![]() பங்களிப்பையும் கருத்தில் கொண்டு, மேற்பொருந்துதல் தத்துவத்தைப் பயன்படுத்தி
கடத்தியினால், P புள்ளியில் உருவாகும் நிகர காந்தப்புலத்தைக் கண்டறியலாம். எனவே சமன்பாடு
(3.34) ஐ தொகைப்படுத்தும்போது
பங்களிப்பையும் கருத்தில் கொண்டு, மேற்பொருந்துதல் தத்துவத்தைப் பயன்படுத்தி
கடத்தியினால், P புள்ளியில் உருவாகும் நிகர காந்தப்புலத்தைக் கண்டறியலாம். எனவே சமன்பாடு
(3.34) ஐ தொகைப்படுத்தும்போது
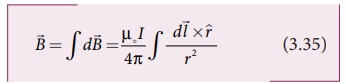
என்று கிடைக்கும். இங்கு முழு மின்னோட்டப்பகிர்விற்கும்
தொகைப்படுத்த வேண்டும்.
சிறப்பு
நேர்வுகள்
1. புள்ளி P கடத்தியின் மீதே அமைந்தால், θ =
0°.எனவே ![]() சுழியாம்.
சுழியாம்.
2. புள்ளி P கடத்திக்கு செங்குத்தாக அமைந்தால்,θ =
90° எனவே ![]() பெருமமாகும். மேலும் இதனை பின்வருமாறு எழுதலாம்.
பெருமமாகும். மேலும் இதனை பின்வருமாறு எழுதலாம்.
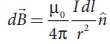 இங்கு n^ என்பது I
இங்கு n^ என்பது I![]() மற்றும் r^ க்குச் செங்குத்தான ஓரலகு வெக்டராகும்.
மற்றும் r^ க்குச் செங்குத்தான ஓரலகு வெக்டராகும்.
குறிப்பு
மின்னோட்டம் ஒரு வெக்டர் அளவல்ல. இது ஒரு ஸ்கேலர்அளவாகும்.
ஆனால் கடத்தியில் பாயும் மின்னோட்டத்திற்கு திசை உண்டு. எனவே கடத்தியின் சிறு கூறில்
பாயும் மின்னோட்டத்தை வெக்டர்- அளவாகக் கருதலாம். அதாவது ![]()
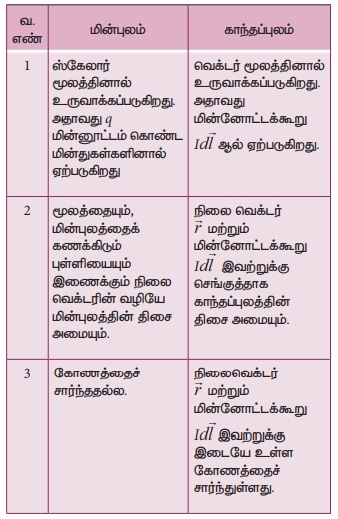
மின்புலம்
(கூலூம் விதியிலிருந்து) மற்றும் காந்தப்புலத்திற்கு (பயட் - சாவர்ட் விதியிலிருந்து)
இடையேயான ஒற்றுமைகள்
• மின்புலம் மற்றும் காந்தப்புலம் ஆகியவை எதிர்த்தகவு
இருமடி விதிக்குக் கட்டுப் படுகின்றன. எனவே இவ்விரண்டும் நீண்ட நெடுக்கமுடைய புலங்களாகும்
(Long range field).
• மேற்பொருந்துதல்தத்துவத்திற்குக் கட்டுப்படுகின்றன.
மேலும் மூலத்தைப் பொருத்து நேர்போக்குத் தன்மை உடையவை. எண்மதிப்பில்,

மின்புலம்
(கூலும் விதியிலிருந்து) மற்றும் காந்தப்புலத்திற்கு (பயட் சாவர்ட் விதியிலிருந்து)
இடையேயான வேறுபாடுகள்
குறிப்பு
மின்னூட்டம் q வின் (மூலத்தின்) அடுக்கும்,
மின்புலம் E இன்அடுக்கும் ஒன்றாக இருக்கும். இதே போன்று மின்னோட்டக்கூறு Idl இன் (மூலத்தின்)
அடுக்கும் காந்தப்புலம் B இன் அடுக்கும் ஒன்றாக இருப்பதை இங்கு கவனிக்க வேண்டும். வேறுவகையாகக்
கூறும்போது மின்புலம் ![]() யானது மின்னூட்டத்திற்கு (மூலத்திற்கு) நேர்த்தகவு. ஆனால்
மின்னூட்டத்தின் உயர் அடுக்குகளுக்கு (q2, q3, ...) நேர்த்தகவல்ல.
இதேபோன்று, காந்தப்புலம் B மின்னோட்டக்கூறு I
யானது மின்னூட்டத்திற்கு (மூலத்திற்கு) நேர்த்தகவு. ஆனால்
மின்னூட்டத்தின் உயர் அடுக்குகளுக்கு (q2, q3, ...) நேர்த்தகவல்ல.
இதேபோன்று, காந்தப்புலம் B மின்னோட்டக்கூறு I![]() (மூலத்திற்கு) நேர்த்தகவு. ஆனால்
மின்னோட்டக்கூறின் உயர் அடுக்குகளுக்கு நேர்த்தகவல்ல. காரணம் மற்றும் விளைவு இவ்விரண்டும்
நேர்ப்போக்குத் தொடர்புடையவைகளாகும்.
(மூலத்திற்கு) நேர்த்தகவு. ஆனால்
மின்னோட்டக்கூறின் உயர் அடுக்குகளுக்கு நேர்த்தகவல்ல. காரணம் மற்றும் விளைவு இவ்விரண்டும்
நேர்ப்போக்குத் தொடர்புடையவைகளாகும்.
2. மின்னோட்டம்
பாயும் நீண்ட நேரான கடத்தியினால் ஏற்படும் காந்தப்புலம்
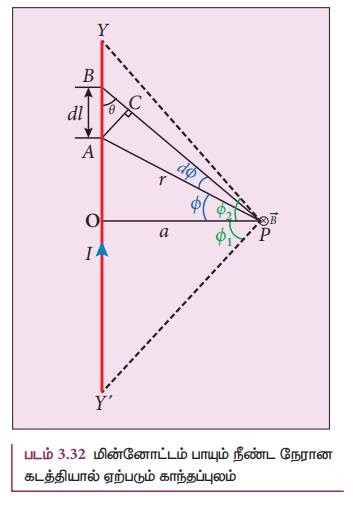
YY' என்ற ஈறிலா நீண்ட நேர்க்கடத்தியில் படம்
3.32ல் கொடுக்கப்பட்டுள்ளது போல் மின்னோட்டம் I பாய்வதாகக் கருதுவோம். கடத்தியிலிருந்து
a தொலைவில் உள்ள புள்ளி Pல் உருவாகும் காந்தப் புலத்தைக் கணக்கிடுவதற்காக dl நீளம்
கொண்ட சிறு கூறு (பகுதி AB) ஒன்றைக் கருதுவோம்.
மின்னோட்டக் கூறு Idl-னால் புள்ளி Pல் உருவாகும்
காந்தப் புலத்தைக் கணக்கிட பயட் - சாவர்ட் விதியைப் பயன்படுத்துவோம்:
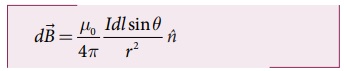
இங்கு n^ என்பது புள்ளி Pல் உள்நோக்கிய
திசையில் செயல்படும் ஓரலகு வெக்டர், θ என்பது
மின்னோட்டக் கூறு Idlக்கும் dl மற்றும் புள்ளி Pஐ இணைக்கும் கோட்டிற்கும் இடைப்பட்ட
கோணம். r என்பது Aல் உள்ள கோட்டுப் பகுதிக்கும் புள்ளி Pக்கும் இடைப்பட்ட தொலைவு.
திரிகோணமிதி சமன்பாடுகளைப் பயன்படுத்த A இலிருந்து
BPக்கு செங்குத்துக்கோடு ஒன்று வரைக (படம் 3.32)
∆ABCல், sin θ =
AC/AB
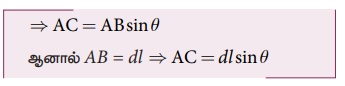
ஆனால் AB = dl ⇒AC=dl sin θ
AP மற்றும் BPக்கு இடையேயுள்ள கோணம்
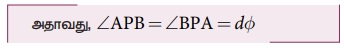

AP மற்றும் OPக்கு இடையேயுள்ள கோணம் Ø என்க,

கடத்தி YY'-ஆல் புள்ளி Pல் ஏற்படும் காந்தப்புலம்
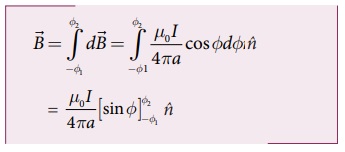
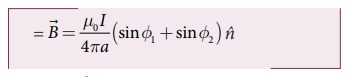
ஈறிலா நீளம் கொண்ட கடத்திக்கு
Ø1 = Ø2 900
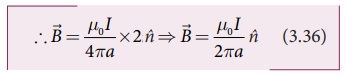
3. மின்னோட்டம்
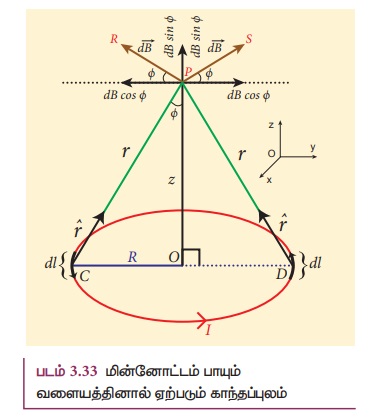
பாயும் வட்டவடிவக் கம்பிச்சுருளின் அச்சு வழியே ஏற்படும் காந்தப்புலம்
R ஆரமுடைய மின்னோட்டம் பாயும் வளைய ஒன்றைக்
கருதுக. இவ்வளையத்தின் வழியே I மின்னோட்டம் பாய்கிறது. இம்மின்னோட்டத்தி. திசை படம்
3.33இல் காட்டப்பட்டுள்ளது.
வளையத்தின் மையம் O விலிருந்து z தொலைவில்
அதன் அச்சின் மீது அமைந்துள்ள புள் P யைக் கருதுக. இப்புள்ளியில் காந்தப்புலத்தை கணக்கிட
வட்ட வளையத்தின் மீது எதிரெதிரா அமைந்துள்ள C மற்றும் D புள்ளிகளில் I![]() நீளமுடைய
இரு நீளக் கூறுகளைக் கருதுக. புள்ளி Cல் உள்ள மின்னோட்டக் கூறு (I
நீளமுடைய
இரு நீளக் கூறுகளைக் கருதுக. புள்ளி Cல் உள்ள மின்னோட்டக் கூறு (I![]() ) மற்றும்
புள்ளி Pயை இணைக்கும் வெக்டரை r^ என்க
) மற்றும்
புள்ளி Pயை இணைக்கும் வெக்டரை r^ என்க
பயட்- சாவர்ட் விதியின் படி மின்னோட்டக் கூறு (I![]() ) ஆல் P புள்ளியில் ஏற்படும் காந்தப்புலம்
) ஆல் P புள்ளியில் ஏற்படும் காந்தப்புலம்

![]() ன் எண்மதிப்பு
ன் எண்மதிப்பு
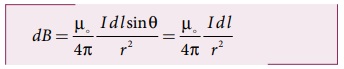
இங்குθ என்பது I![]() மற்றும்
மற்றும் ![]() ஆகியவற்றிற்கு இடைப்பட்ட கோணம்; இங்குθ =
90° ஆகும்.
ஆகியவற்றிற்கு இடைப்பட்ட கோணம்; இங்குθ =
90° ஆகும்.
![]() ன் திசை மின்னோட்டக் கூறு I
ன் திசை மின்னோட்டக் கூறு I![]() மற்றும்
CP ஆகியவற்றிற்கு செங்குத்தாக இருக்கும். அதாவது, அது CPக்கு குத்தாக PR திசையில் இருக்கும்.
மற்றும்
CP ஆகியவற்றிற்கு செங்குத்தாக இருக்கும். அதாவது, அது CPக்கு குத்தாக PR திசையில் இருக்கும்.
புள்ளி Dல் உள்ள மின்னோட்டக் கூறினால் Pல்
ஏற்படும் காந்தப்புலத்தின் எண்மதிப்பு புள்ளி Cல் உள்ள மின்னோட்டக் கூறினால் Pல் ஏற்படும்
காந்தப்புலத்தின் எண்மதிப்புக்கு சமம் ஆகும். ஏனெனில் அவையிரண்டும் சம் தொலைவில் உள்ளன.
ஆனால் இக்காந்தப்புலம் PS திசையில் இருக்கும்.
ஒவ்வொரு மின்னோட்டக் கூறினாலும் ஏற்படும் காந்தப்புலம் ![]() ஐ y திசையில் dBcosØ என்றும் Z - திசையில் dBsinØ என்றும் இரண்டு
கூறுகளாகப் பிரிக்கலாம். கிடைத்தளக் கூறுகள் ஒன்றையொன்று சமன் செய்து கொள்ளும். எனவே
செங்குத்துக் கூறுகள்
ஐ y திசையில் dBcosØ என்றும் Z - திசையில் dBsinØ என்றும் இரண்டு
கூறுகளாகப் பிரிக்கலாம். கிடைத்தளக் கூறுகள் ஒன்றையொன்று சமன் செய்து கொள்ளும். எனவே
செங்குத்துக் கூறுகள்  மட்டுமே புள்ளி Pல் ஏற்படும் மொத்த காந்தப்புலத்திற்கும்
காரணமாக அமைகின்றன.
மட்டுமே புள்ளி Pல் ஏற்படும் மொத்த காந்தப்புலத்திற்கும்
காரணமாக அமைகின்றன.
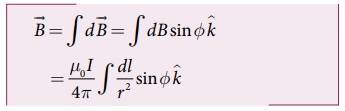
∆OCPலிருந்து

இம்மதிப்புகளை மேலே உள்ள சமன்பாட்டில் பிரதியிட,
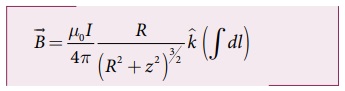
மின்னோட்டம் பாயும் வட்டச்சுருளினால் புள்ளி
Pல் உருவாகும் நிகர காந்தப்புலம் ![]() ஐக் கணக்கிட நீளக்கூறினை 0 இலிருந்து 2πR வரை
தொகையிடவும்.
ஐக் கணக்கிட நீளக்கூறினை 0 இலிருந்து 2πR வரை
தொகையிடவும்.
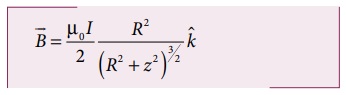
வட்டச்சுருள் N சுற்றுகளைக் கொண்டது எனில்,
காந்தப்புலம்
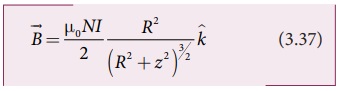
சுருளின் மையத்தில் காந்தப்புலம்

எடுத்துக்காட்டு
3.13
படத்தில் காட்டப்பட்டுள்ள வளையத்தின் மையத்தில்
ஏற்படும் காந்தப்புலத்தைக் காண்க?
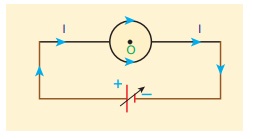
தீர்வு
வளையத்தின் மேல் அரைவட்டத்தின் மற்றும் கீழ்
அரைவட்டத்தின் வழியே மின்னோட்டம் பாய்வதால் ஏற்படும் காந்தப்புலங்கள் எண்மதிப்பில்
சமமாகவும் எதிரெதிர் திசைகளில் செயல்படுவதால், வளையத்தின் மையத்தில் (O புள்ளியில்)
நிகர காந்தப்புலம் ![]() சுழியாகும்
சுழியாகும் ![]() =
= ![]()
4. டேஞ்சன்ட் விதி
மிகக்குறைந்த மின்னோட்டங்களை அளவிடும் ஒரு
கருவி டேஞ்சன்ட் கால்வனோமீட்டர் ஆகும் (படம் 3.34) டேஞ்சன்ட் விதியின் அடிப்படையில்
இக்கருவி இயங்குகிறது. இது ஒரு நகரும் காந்த கால்வனோமீட்டராகும்.

டேஞ்சன்ட்
விதி
ஒன்றுக்கொன்று
செங்குத்தாகச் செயல்படும் சீரான இரண்டு காந்தப்புலங்களுக்கு நடுவே தொங்கவிடப்பட்டுள்ள
காந்த ஊசி, இவ்விரண்டு புலங்களின் தொகுபயன் புலத்தின் திசையில் நிற்கும்.
டேஞ்சன்ட் கால்வனோமீட்டரின் கம்பிச்சுருள்
வழியாக மின்னோட்டம் பாய்வதால் ஏற்படும் காந்தப்புலத்தை B என்க. புவிகாந்தப்புலத்தின்
கிடைத்தளக் கூறு BH ஆகும். இவ்விரண்டு காந்தப்புலங்களின் செயல்பாட்டால்
காந்த ஊசி கிடைத்தளக்கூறு BH உடன்θ கோணத்தை
ஏற்படுத்தி ஓய்வு நிலையை அடையும், எனவே

அமைப்பு
டேஞ்சன்ட்கால்வனோமீட்டரில் காந்தத்தன்மையற்ற
வட்டவடிவ சட்டத்தின் மீது தாமிரக்கம்பிச்சுருள் சுற்றப்பட்டிருக்கும். இச்சட்டம் பித்தளை
அல்லது மரத்தால் செய்யப்பட்டு கிடைத்தள மேடைக்கு (சுழல் மேடைக்கு) செங்குத்தாகப் பொருத்தப்பட்டிருக்கும்.
இம்மேடை சரிசெய்யும் மூன்று கிடைமட்டத் திருகுகளைப் பெற்றுள்ளது. வெவ்வேறு எண்ணிக்கையில்
அமைந்த இரண்டு அல்லது மூன்று கம்பிச்சுருள்கள் டேஞ்சன்ட் கால்வனோமீட்டரில் பொருத்தப்பட்டுள்ளன.
நாம் ஆய்வுக்கூடங்களில்பயன்படுத்தும் பெரும்பாலானவற்றில் 2 சுற்றுகள், 5 சுற்றுகள்
மற்றும் 50 சுற்றுகள் கொண்ட வெவ்வேறு தடிமனுடைய கம்பிச்சுருள்கள், வெவ்வேறு வலிமை கொண்ட
மின்னோட்டங்களை அளவிட பயன்படுத்தப்படுகின்றன.
சுழல் மேடைக்கு நடுவே சற்றே மேலெழும்பிய அமைப்பு
உள்ளது அதில் காந்த ஊசிப்பெட்டி (விலகு காந்தமானி) பொருத்தப்பட்டுள்ளது. காந்த ஊசிப்
பெட்டியின் உள்ளே கூர்முனையின் மீது பொருத்தப்பட்ட காந்த ஊசி ஒன்று உள்ளது. காந்த ஊசியின்
மையமும், வட்டவடிவக்கம்பிச்சுருளின் மையமும் மிகச்சரியாக ஒன்றுடன் ஒன்று பொருந்தும்
வகையில் இவ்வமைப்பு வடிவமைக்கப்பட்டுள்ளது. மெல்லிய அலுமினியக்குறிமுள் ஒன்று காந்த
ஊசிக்கு செங்குத்தாக, வட்ட அளவுகோலின் மீது சுழலும்படி இணைக்கப்பட்டுள்ளளது. வட்ட அளவுகோல்
நான்கு கால்வட்டங்களாகப் பிரிக்கப்பட்டு டிகிரி அளவீடுகள் குறிக்கப்பட்டுள்ளன. இந்த
அளவீட்டினைப் பயன்படுத்தி வட்ட அளவுகோலின் மீது குறிமுள்ளின் விலக்கத்தை அளக்கலாம்.
இடமாறு தோற்றப்பிழையைத் தவிர்க்க, குறிமுள்ளுக்கு கீழே கண்ணாடி பொருத்தப்பட்டுள்ளது.
கருவியை
பயன்படுத்தும்போது மேற்கொள்ள வேண்டிய முன்னெச்சரிக்கை நடவடிக்கைகள்
1. கருவியின் அருகில் உள்ள அனைத்து காந்தப்
பொருட்களையும் அகற்ற வேண்டும்.
2. இரச மட்டத்தைப் பயன்படுத்தி (Sprit
level), கிடைமட்டத் திருகுகளை சரிசெய்ய வேண்டும். அவ்வாறு சரி செய்யும் போது மிகச்சரியாக
காந்த ஊசி கிடைத்தளத்திலும், சட்ட காந்தத்தின் மீது சுற்றப்பட்ட கம்பிச்சுருள் செங்குத்தாகவும்
அமையும்.
3. கம்பிச்சுருளின் செங்குத்து அச்சைப்பொருத்து
அதனைச் சுழற்றி, கம்பிச்சுருளின் தளம் காந்த ஊசிக்கு இணையாக வரும்படி அதனை அமைக்க வேண்டும்.
அவ்வாறு அமைக்கும் போது கம்பிச்சுருள் தொடர்ந்து காந்த துருவத் தளத்திலேயே இருக்கும்.
4. காந்த ஊசிப்பெட்டியைச் சுழற்றி, குறிமுள்
0° - 0°ஐக் காட்டும்படி அமைக்க வேண்டும்.
கொள்கை
கம்பிச்சுருளின் வழியே மின்னோட்டம் பாயாத நிலையில்
காந்த ஊசி புவிகாந்தப்புலத்தின் கிடைத்தளக்கூறின்திசையிலேயே ஒருங்கமைந்திருக்கும்.மின்சுற்றினை
இயக்கும்போது கம்பிச்சுருளின் வழியேமின்னோட்டம் பாய்ந்து காந்தப்புலத்தை உருவாக்கும்.
சுழலும் மின்னோட்டத்தினால் எவ்வாறு காந்தப்புலம் உருவாகின்றது என்பதை பிரிவு 3.8.3
இல் விரிவாகப்படிக்கப் போகிறீர்கள். தற்போது ஒன்றுகொன்று செங்குத்தாகச் செயல்படும்
இரண்டு காந்தப்புலங்கள் உருவாகும் அவை
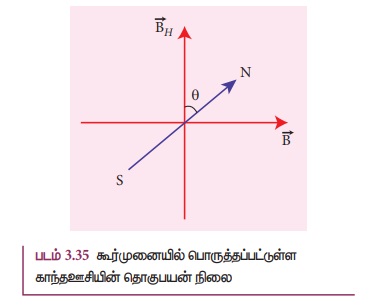
(1) மின்னோட்டம் பாயும் கம்பிச்சுருளின்தளத்திற்குச்
செங்குத்தாக செயல்படும்காந்தப்புலம் (B)
(2) புவி காந்தப்புலத்தின் கிடைத்தளக்கூறு
(BH).
ஒன்றுக் கொன்று செங்குத்தாகச் செயல்படும் இவ்விரண்டு
காந்தப்புலங்களுக்கு நடுவே கூர்முனையில் பொருத்தப்பட்டுள்ள காந்த ஊசி 0 கோண அளவு விலகலை
ஏற்படுத்தும். சமன்பாடு (3.39) இல் குறிப்பிட்டுள்ள டேஞ்சன்ட் விதியிலிருந்து

R ஆரமும் N சுற்றுகளும் கொண்ட வட்டவடிவக் கம்பிச்சுருளின்
வழியே மின்னோட்டம் பாய்வதால் அதன் மையத்தில் தோன்றும் காந்தப்புலம்

சமன்பாடுகள் (3.39) மற்றும் (3.40) ஆகியவற்றிலிருந்து
நாம் பெறுவது,

மேற்கண்ட சமன்பாட்டிலிருந்து பெறப்பட்ட புவிகாந்தப்புலத்தின்
கிடைத்தளக்கூறு

எடுத்துக்காட்டு
3.14
100 சுற்றுகள் கொண்ட டேஞ்சன்ட் கால்வனோ மீட்டர்
ஒன்றின் கம்பிச்சுருளின் விட்டம் 0.24 m. புவிகாந்தப்புலத்தின் கிடைத்தள கூறின் மதிப்பு
25 X 10-6 T என்ற நிலையில், 600 விலக்கத்தை ஏற்படுத்தும் மின்னோட்டத்தைக்
கணக்கிடுக.
தீர்வு
கம்பிச்சுருளின் விட்டம் 0.24 m எனவே அதன்
ஆரம் 0.12 m ஆகும். சுற்றுகளின் எண்ணிக்கை 100
புவிகாந்தப்புலத்தின் மதிப்பு = 25 x 10-6
T
விலக்கம்
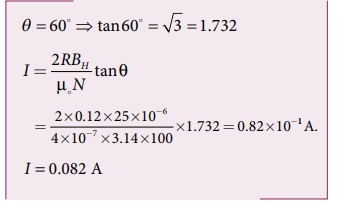
5. மின்னோட்ட வளையம் காந்த இருமுனையாக செயல்படல்
R ஆரம் கொண்ட மின்னோட்டம் பாயும் வட்ட வளையத்தின்
அச்சில் அதன் மையத்திலிருந்து z தொலைவிலுள்ள புள்ளியில் உருவாகும் காந்தப்புலம்

வட்ட வளையத்தின் பரப்பு A எனில், A = πR2எனவே
சமன்பாடு (3.41) ஐ பரப்பினைப் பொறுத்து எழுதும்போது

சமன்பாடு (3.43) மற்றும் (3.14) ஐ பரிமாணமுறையில்
ஒப்பிடும் போது
Pm= I A
இங்கு pm என்பது காந்த இருமுனை
திருப்புத் திறனைக் குறிக்கும். வெக்டர் குறியீட்டின்படி

இச்சமன்பாட்டிலிருந்து மின்னோட்டம் பாயும்
வளையமானது காந்தத்திருப்புத்திறன் ![]() கொண்ட காந்த இருமுனையாக செயல்படும் என
அறியலாம்.
கொண்ட காந்த இருமுனையாக செயல்படும் என
அறியலாம்.
எனவே, எந்த ஒரு மின்னோட்ட வளையத்தின் காந்த
இருமுனை திருப்புத்திறன் அம்மின்னோட்ட வளையத்தில் பாயும் மின்னோட்டம் மற்றும் மின்னோட்ட
வளையத்தின் பரப்பு இவற்றிற்கிடையேயான பெருக்கல் பலனுக்குச் சமமாகும்.
வலதுகை
பெருவிரல் விதி
காந்தத்திருப்புத்திறனின் திசையை அறிய நாம்
வலதுகை பெருவிரல் விதியைப் பயன்படுத்தலாம்.
இவ்விதியின்படி
வளையத்தின் வழியே பாயும் மின்னோட்டத்தின் திசையில் வலதுகையின் மற்ற விரல்களால் வளையத்தை
சுற்றி பற்றும் போது, நீட்டப்பட பெருவிரல் அம்மின்னோட்ட வளையத்தினால் உருவாகும் காந்தத்திருப்புத்திறனின்
திசையைக் கொடுக்கும்.
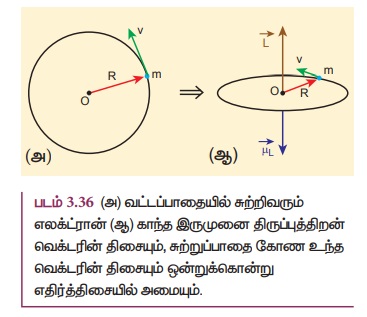
6. சுற்றிவரும் எலக்ட்ரானின் காந்த இருமுனைத் திருப்புத்திறன்
உட்கரு ஒன்றினை வட்டப்பாதையில் எலக்ட்ரான்
ஒன்று சுற்றி வருவதாகக் கொள்வோம். இந்த வட்டப்பாதையில் சுற்றி வரும் எலக்ட்ரானை, வளையத்தில்
பாயும் மின்னோட்டம் போன்று கருதலாம். இது படம் 3.36 இல் காட்டப்பட்டுள்ளது. ஏனெனில்
மின் துகள்களின் ஓட்டமே மின்னோட்டமாகும். எனவே மின்னோட்டம் பாயும் வளையத்தின் காந்த
இருமுனைத் திருப்புத்திறன்

எண்மதிப்பில்,

T என்பது எலக்ட்ரானின் அலைவு நேரம் எனக் கொண்டால்,
வட்டப்பாதையில் சுற்றிவரும் எலக்ட்ரானால் ஏற்படும் மின்னோட்டம்

இங்கு e என்பது எலக்ட்ரானின் மின்னூட்டமாகும்.
வட்டப்பாதையின் ஆரம் R மற்றும் வட்டப்பாதையில் சுற்றிவரும் எலக்ட்ரானின் திசைவேகம்
v எனவும் கொண்டால்

சமன்பாடுகள் (3.46) மற்றும் (3.47) ஐ சமன்பாடு
(3.45) இல் பயன்படுத்தும்போது,
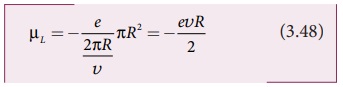
இங்கு A = πR2
வளையத்தின் பரப்பாகும். வரையறையின்படி, O வைப் பொறுத்து எலக்ட்ரானின் கோண உந்தம்

எண்மதிப்பில்,

சமன்பாடு (3.48) மற்றும் (3.49) ஐ பயன்படுத்தி
பின்வரும் சமன்பாட்டைப் பெறலாம்.
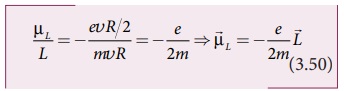
காந்தத்திருப்புத்திறன் மற்றும் கோண உந்தம்
இரண்டின் திசையும் ஒன்றுக்கொன்று எதிரெதிர் என்பதை எதிர்க்குறி நமக்குக் காட்டுகிறது.
எண்மதிப்பில்,
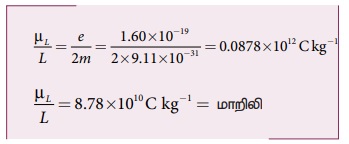
μL/L விகிதம்
ஒரு மாறிலியாகும். மேலும் இதனை சுழற்சி காந்த விகிதம் (gyro-magnetic ratio)(e/2m)
என அழைக்கலாம். சுழற்சி காந்த விகிதம் ஒரு விகித மாறிலி என்பதை நினைவில் கொள்ளவும்.
இது எலக்ட்ரானின் கோண உந்தத்தையும், காந்தத்திருப்புத்திறனையும் இணைக்கிறது.
நீல்ஸ் போரின் குவாண்டமாக்கல் நிபந்தனையின்படி
நிலையான சுற்றுப்பாதையில் சுற்றிவரும் எலக்ட்ரானின் கோண உந்தம் குவாண்டமாக்கப்பட்டுள்ளது.
அதாவது,

இங்கு , h என்பது பிளாங்க் மாறிலி ஆகும்.
(h = 6.63x 10-34 Js) மற்றும் n என்பது நேர்க்குறி முழு எண்க ளைக் குறிக்கும்.
அதாவது n = 1,2,3,.....
எனவே,

சிறும காந்தத்திருப்புத்திறனைக் கண்டறிய n
= 1 எனப் பிரதியிட வேண்டும்.
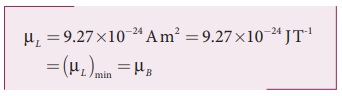
இங்கு μB = eh/4 π m இதனை போர் மேக்னெட்டான் (Bohr magneton) என்று அழைக்கலாம்.