காந்தவியல் ஓர் அறிமுகம்

அலகு 3

காந்தவியல் மற்றும் மின்னோட்டத்தின் காந்தவிளைவுகள்

“காந்தவிசை உயிர்போன்றது அல்லது ஆன்மாவை ஒத்தது; உயிரோட்டமுள்ள உடலில் ஒருமுகப்படுத்தப்பட்டுவெளிப்படும்போது பல வகைகளில் அது மனித ஆன்மாவையே விஞ்சி விடுகிறது!”

                                                                                    - வில்லியம் கில்பர்ட்

கற்றலின் நோக்கங்கள்:

இந்த அலகில் மாணவர்கள் அறிந்துகொள்வது

• புவிகாந்தப்புலம் மற்றும் காந்தக்கூறுகள்

• காந்தங்களின் அடிப்படைப் பண்புகள்

•காந்தவியல் கூலூம் எதிர்த்தகவு இருமடி விதியின் கூற்று

• காந்த இருமுனை

• சட்டகாந்தத்தின் அச்சுக்கோடு மற்றும் நடுவரைக் கோட்டில் ஏதேனும் ஒரு புள்ளியில் ஏற்படும் காந்தப்புலம்

• சீரான காந்தப்புலத்தில் உள்ள ஒரு சட்டகாந்தத்தின் மீது செயல்படும் திருப்புவிசை

• காந்தப்பண்புகள் - காந்த உட்புகுதிறன், காந்த ஏற்புத்திறன் மற்றும் சில

• காந்தப்பொருட்களின் வகைப்பாடு - டயா, பாரா மற்றும் ஃபெர்ரோ காந்தப்பொருட்கள்

• காந்தத்தயக்கம் பற்றிய கருத்து

• மின்னோட்டத்தின் காந்த விளைவுகள் – நீண்ட நேரான கடத்தி மற்றும் வட்டவடிவக் கம்பிச்சுருள்

• வலதுகை பெருவிரல் விதி மற்றும் மேக்ஸ்வெல்லின் வலதுகை திருகுவிதி

• பயட் - சாவர்ட்விதி மற்றும் அதன் பயன்பாடுகள்

• டேஞ்சன்ட் விதி மற்றும் டேஞ்சன்ட் கால்வனோமீட்டர்

• மின்னோட்ட சுற்று காந்த இருமுனையாக செயல்படல்

• சுற்றிவரும் எலக்ட்ரானின் காந்த இருமுனைத்திருப்புத்திறன்

• ஆம்பியர் சுற்றுவிதி மற்றும் அதன் பயன்பாடுகள்

• வரிச்சுருள் மற்றும் வட்ட வரிச்சுருள்

• லாரன்ஸ் விசை - மின்காந்தப்புலத்தில் இயங்கும் மின்துகள்

• சைக்ளோட்ரான்

• காந்தப்புலத்தில் உள்ள மின்னோட்டம் பாயும் கடத்தியின் மீது செயல்படும் விசை

• மின்னோட்டம் பாயும் இரு நீண்ட இணை கடத்திகளுக்கிடையே ஏற்படும் விசை

• காந்தப்புலத்தில் உள்ள மின்னோட்ட சுற்று மீது ஏற்படும் திருப்புவிசை

• இயங்கு சுருள் கால்வனோமீட்டர்

காந்தவியல் ஓர் அறிமுகம்

காந்தம்! அதன் தன்மையினால் அனைவரையும் ஈர்க்கும் என்பதில் எந்த ஐயமும் இல்லை. காந்தத்தின் பயங்களைக் கொண்டு இந்த உலகம் நவீன சொகுசு வாழ்க்கையை அனுபவிக்கிறது. பல நூற்றாண்டுகளாக காந்தம் பற்றிய படிப்பானது உலகம் முழுவதும் உள்ள பல்வேறு அறிவியல் அறிஞர்களுக்கு கவர்ந்திழுக்கக் கூடியதாக இருந்து வந்துள்ளது. இன்றும் கூட காந்தம் பற்றிய ஆய்வுகள் தொடர்ந்து கொண்டே உள்ளன (படம் 3.1)

உங்களுக்குத் தெரியுமா?

புவிகாந்தப்புலத்தைப் பயன்படுத்தி திசை அறிவதற்காக, பெரும்பான்மையான பறவைகளும், விலங்குகளும் அவற்றின் கண்களில் காந்த நுண் உணர்வுகளைப் பெற்றுள்ளன.

கண்களின் காந்த நுண் உணர்வு - ஜீப்ராபின்ச் (Zebrafinch) என்ற பறவை, அதன் விழித்திரையில் உள்ள கிரிப்டோகுரோம்ஸ் (Protein Cryptochromes - Cry 4) என்ற புரதத்தைக் கொண்டு, புவிகாந்தப்புலத்தை உணர்ந்து அது பறக்கும் திசையை அறிந்துகொள்கிறது.

எலக்ட்ரான் போன்ற நுண்துகளிலிருந்து, பிரபஞ்சம் வரை எங்கும் காந்தவியல் நீக்கமற நிறைந்துள்ளது.வரலாற்றுப்பூர்வமாக மேக்னட்டிஸம் (Magnetism) என்ற வார்த்தை, மேக்னடைட் (Magnetite) (Fe₃ O₄) என்ற இரும்புத்தாதுவின் பெயரிலிருந்து உருவானதாகும். பழங்காலத்தில் காந்தங்கள் திசைகாட்டும் கருவிகளை தயாரிக்கவும், காந்த சிகிச்சைக்காகவும் மற்றும் தந்திரக்காட்சிகளை செய்து காட்டவும் பயன்பட்டன.

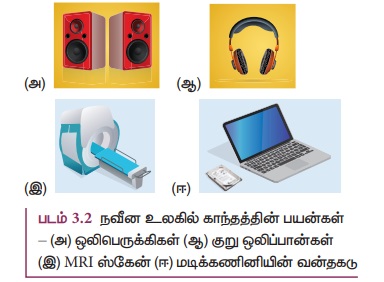
நவீன உலகில், நாம் அன்றாடம் பயன்படுத்தும் பெரும்பாலான பொருட்களில் காந்தங்கள் உள்ளன. மின் இயந்திரங்கள், மிதிவண்டி மின்னியற்றிகள், ஒலிபெருக்கிகள், ஒலி மற்றும் ஒளிப்பதிவிற்குப் பயன்படும் காந்த நாடாக்கள், அலைபேசிகள், குறுஒலிப்பான்கள் (head phones), குறுந்தகடுகள், பேனா வடிவ சேமிப்பான்கள் (Pendrive), மடிக்கணினியில் உள்ள வன்தகடுகள், குளிர்பதனப்பெட்டியின் கதவுகள், மின்னியற்றிகள் போன்றவை இதற்கு சில உதாரணங்களாகும். இவற்றில் சில படம் 3.2 இல் காட்டப்பட்டுள்ளன.

நெடுங்காலமாக, மின்னியல் மற்றும் காந்தவியல் இரண்டும் ஒன்றுடன் ஒன்று தொடர்பற்ற இயற்பியலின் இருவேறு பிரிவுகள் என நம்பப்பட்டது. 1820 இல், மின்னோட்டம் பாயும் கம்பிக்கு அருகே காந்த ஊசிப்பெட்டியை (திசைகாட்டும் கருவி) கொண்டுவரும்போது அது விலகலடையும் என்ற H.C ஆர்ஸ்டேட்டின் கண்டுபிடிப்பு மின்னியல் மற்றும் காந்தவியல் என்று பிரிந்திருந்த இவ்விரண்டு பிரிவுகளையும் மின்காந்தவியல் என்ற இயற்பியலின் ஒரே பிரிவாக ஒருங்கிணைத்தது.

இந்த அலகில், காந்தங்கள் பற்றிய அடிப்படை மற்றும் அவற்றின் பண்புகள் கொடுக்கப்பட்டுள்ளன. மேலும், மாறா மதிப்புள்ள மின்னோட்டம் பாயும் கடத்தி எவ்வாறு காந்தம் போன்று செயல்படுகிறது என்று விவரிக்கப்பட்டுள்ளது.

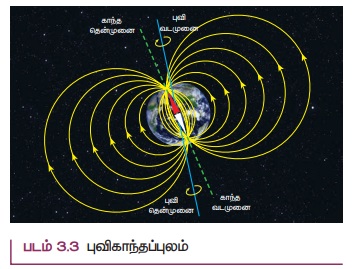
1. புவிகாந்தப்புலம் மற்றும் புவிகாந்தப்புலக் கூறுகள்

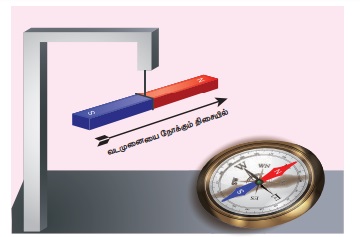
திசை காட்டும் கருவியில் உள்ள காந்த ஊசி அல்லது தடையின்றி தொங்கவிடப்பட்ட காந்தம் போன்றவை கிட்டத்தட்ட புவியின், வடக்கு - தெற்கு திசையில் நிற்பதை சிறுவகுப்பில் நாம் நிகழ்த்திய சோதனைகளில் மூலம் அறிந்திருப்போம்.

திசை காட்டும் காந்த ஊசியின் வடமுனை, புவியின் வடமுனைக்கு அருகே உள்ள காந்த தென்முனையால் ஈர்க்கப்படுகிறது (படம் 3.3). இதேபோன்று காந்த ஊசியின் தென்முனை,

உங்களுக்குத் தெரியுமா?

1600- ஆம் ஆண்டில் வாழ்ந்தவில்லியம் கில்பர்ட் என்ற அறிஞர்,புவி ஒரு மிகப்பெரிய ஆற்றல் வாய்ந்த சட்ட காந்தம் போன்று செயல்படுகிறது என்ற கொள்கையை முன்மொழிந்தார். ஆனால் இக்கொள்கை ஏற்றுக்கொள்ளப்படவில்லை. ஏனெனில், புவியின் உள்ளே உள்ள மிக உயர்ந்த வெப்பநிலையில், அக்காந்தம், அதன் காந்தத்தன்மையை இழந்துவிடும்.

சூரியனிடமிருந்து வரும் வெப்பக்கதிர்கள் தான் புவியின் காந்தப்புலத்திற்குக் காரணம் என்று கோவர் (Gover) என்ற அறிஞர் முன்மொழிந்தார். இக்கதிர்கள் பூமத்தியரேகைப் பகுதியின் (equatorial region) அருகே உள்ள காற்றை வெப்பப்படுத்தும். இந்த வெப்பக் காற்று புவியின் வட மற்றும் தென் அரைக்கோளங்களை நோக்கி வீசும்போது மின்னேற்றம் அடைகிறது. புவிப்பரப்பிலுள்ள ஃபெர்ரோ காந்தப் பொருட்கள் காந்தத்தன்மையை அடைவதற்கு இந்த மின்னேற்றம் பெற்ற வெப்பக்காற்றே காரணமாக இருக்கலாம். இன்றுவரை புவியின் காந்தத்தன்மையை விளக்குவதற்கு பல்வேறு கொள்கைகள் முன்மொழியப்பட்டன. ஆனால் எந்த ஒரு கொள்கையும் புவியின் காந்தத்தன்மைக்கான காரணத்தை முழுமையாக விளக்கவில்லை.

புவியின் தென்முனைக்கு அருகே உள்ள காந்த வடமுனையால் ஈர்க்கப்படுகிறது. புவியின் காந்தப்புலம்பற்றி படிக்கும் இயற்பியலின் பிரிவிற்கு புவிகாந்தவியல் (Geomagnetism) அல்லது நில காந்தவியல் (Terrestrial magnetism) என்று பெயர். புவிப்பரப்பிலுள்ள அதன் காந்தப்புலத்தை குறிப்பிடுவதற்கு மூன்று அளவுகள் தேவைப்படுகின்றன. அவற்றை சில நேரங்களில் புவிக்காந்தப்புலத்தின் கூறுகள் என்றும் அழைக்கலாம். அவை

(அ) காந்த ஒதுக்கம் D (magnetic declination)

(ஆ) காந்தச் சரிவு I (Magnetic dip or inclination)

(இ) புவிகாந்தப்புலத்தின் கிடைத்தளக்கூறு B_H (horizontal component of the Earth's magnetic field)

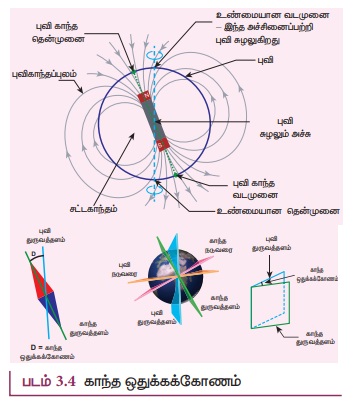
புவி அச்சைப் பொறுத்து, புவி தன்னைத்தானே சுற்றுவதால் இரவு-பகல் ஏற்படுகிறது. இப்புவி அச்சு (Geographic axis) வழியாகச் செல்லும் செங்குத்துத் தளத்திற்கு புவி துருவத்தளம் என்று பெயர். இப்புவி அச்சுக்கு செங்குத்தாகக் கருதப்படும் ஓர் மிகப்பெரியவட்டக் கோட்டிற்கு புவி நடுவரை அல்லது பூமத்தியரேகை என்று பெயர்.

புவிகாந்தமுனைகளை இணைக்கும் நேர்க்கோட்டிற்கு, காந்த அச்சு என்று பெயர். இந்த காந்த அச்சு வழியாகச் செல்லும் செங்குத்துத் தளத்திற்கு காந்த துருவத்தளம் என்று பெயர். புவியின் காந்த அச்சுக்கு செங்குத்தாகக் கருதப்படும் ஓர் மிகப்பெரிய வட்டக் கோட்டிற்கு காந்த நடுவரை அல்லது காந்த மத்தியரேகை என்று பெயர்.

காந்த ஊசி ஒன்றினை தடையின்றி தொங்கவிடும்போது, அக்காந்த ஊசி படம் 3.4 இல் காட்டப்பட்டுள்ள புவி துருவத்தளத்தில் மிகச்சரியாக நிற்காது. புள்ளி ஒன்றில் காந்த துருவத் தளத்திற்கும், புவி துருவத்தளத்திற்கும் இடையே உள்ள கோணம் காந்த ஒதுக்கம் (D) என அழைக்கப்படுகிறது. உயர்ந்த குறுக்கு கோடுகளுக்கு காந்த ஒதுக்கம் பெருமமாகும். ஆனால் புவி நடுவரைக்கு அருகில் இதன் மதிப்பு சிறுமமாகும். இந்தியாவில் காந்த ஒதுக்கம் மிகச்சிறிய மதிப்பைப் பெற்றுள்ளது. மேலும் சென்னையில் இதன் மதிப்பு -1°16' (இது எதிர்க்குறிமதிப்பு (மேற்கு))

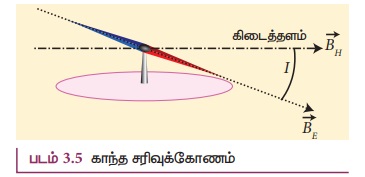
புள்ளி ஒன்றில், புவியின் மொத்த காந்தப்புலம்  காந்தத் துருவத்தளத்தின் கிடைத்தளத்திசையுடன் ஏற்படுத்தும் கோணம், சரிவு அல்லது காந்தச் சரிவு (I) என அழைக்கப்படும். (படம் 3.5). சென்னையின் சரிவுக்கோணம் 14° 28' ஆகும். காந்த துருவத்தளத்தின் கிடைத்தளத்திசையில் உள்ள புவிக்காந்தப்புலத்தின் கூறு, புவிகாந்தப்புலத்தின் கிடைத்தளக்கூறு B_H என்று அழைக்கப்படும்.

புவிப்பரப்பில் P என்ற புள்ளியில் உள்ள புவியின் காந்தப்புலம் B_E என்க. இதனை ஒன்றுக்கொன்று செங்குத்தான இரு கூறுகளாகப் பகுக்கலாம்.

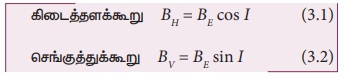
சமன்பாடு (3.2) ஐ (3.1) ஆல் வகுக்கும் போது கிடைப்பது

(i) காந்த நடுவரையில் புவிக்காந்தப்புலம்

புவிக் காந்தப்புலம், புவிப்பரப்பிற்கு இணையாக உள்ளதால். (அதாவது கிடைத்தளமாக) திசைக்காட்டும் கருவியின் குறிமுள் I= 0^o என்ற சரிவுக்கோணத்தில் ஓய்வுநிலையை அடையும்.

நடுவரையில், கிடைத்தளக்கூறு பெருமமாகவும், செங்குத்துக்கூறு சுழியாகவும் இருப்பதை இது உணர்த்துகிறது.

(ii) காந்த துருவங்களில் புவிக்காந்தம்

புவிகாந்தபுலம், புவிப்பரப்பிற்கு செங்குத்தாக உள்ளதை திசைக்காட்டும் கருவியின் குறிமுள்செங்குத்தாக I=90^o என்ற சரிவுக்கோணத்தில் ஓய்வு நிலையை அடைவதிலிருந்து நாம் அறிந்து கொள்ளலாம்.

B_H = 0

B_V = B_E

காந்தத் துருவங்களில், செங்குத்துக்கூறு பெருமமாகவும் கிடைத்தளக்கூறு சுழியாகவும் இருப்பதை இது உணர்த்துகிறது.

எடுத்துக்காட்டு 3.1

ஒரு குறிப்பிட்ட இடத்தில் புவிக்காந்தப்புலத்தின் கிடைத்தளக்கூறு மற்றும் செங்குத்துக்கூறுகள் முறையே 0.15 G மற்றும் 0.26 G எனில், அந்த இடத்தின் காந்த சரிவுக் கோணம் மற்றும் தொகுபயன் காந்தப்புலம் ஆகியவற்றைக் கணக்கிடுக.

(இங்கு  G-gauss. CGS முறையில்  காந்தப்புலத்தின் அலகு காஸ் ஆகும். 1G = 10^-4T)

தீர்வு

B_H = 0.15 G மற்றும் B_V = 0.26 G

tan I = 0.26/0.15 ⇒ I = tan^-1(1.732)=60^o

புவியின் தொகுபயன் காந்தப்புலம்

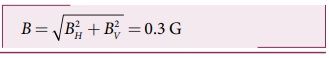
உங்களுக்குத்  தெரியுமா?

வடதுருவ ஒளித்தோற்றம் (Aurora Borealis) மற்றும்தென்துருவ ஒளித்தோற்றம் (Aurora Australias)

உயர்ந்த குறுக்குக் கோட்டுப் பகுதியில் வசிக்கும் மக்கள் (ஆர்டிக் அல்லது அண்டார்டிக் பகுதிக்குஅருகில்) இரவு வானில் பளிச்சிடும் வெளிர் நீல ஒளி தோன்றுவதை கண்டிருப்பார்கள். வானில் தோன்றும் இந்த ஆச்சரியமான காட்சிக்கு வடதுருவ ஒளித்தோற்றம் அல்லது தென் துருவ ஒளித்தோற்றம் என்று பெயர். சில நேரங்களில் துருவ ஒளி என்றும் இதனை அழைப்பார்கள். புவியின் வடக்கு அரைக்கோளம் மற்றும் தெற்கு அரைக்கோளங்களின் காந்தத் துருவங்களுக்கு மேல் இந்த ஒளிக்காட்சியைக் காணலாம். வடக்குதிசையில் இதனை வடதுருவ ஒளித்தோற்றம் என்றும் தெற்குத்திசையில் இதனை தென் துருவ ஒளித்தோற்றம் என்றும் அழைக்கப்படுகிறது. புவியின் வளிமண்டலத்தில் உள்ள வாயுத்துகள்கள், சூரியக்காற்றினால் (Solar wind) சூரியனின் வளிமண்டலத்திலிருந்து வெளியிடப்படும் அதிகமாக மின்னூட்டப்பட்ட துகள்களுடன் இடைவினை புரிவதால் இந்த ஒளித்தோற்றம் ஏற்படுகிறது. மேலும் வெவ்வேறு வகையான துகள்களின் மோதலினால் வெவ்வேறு நிறங்களில் ஒளி தோன்றுகிறது. அயனி நிலையில் உள்ள ஆக்ஸிஜன் மூலக்கூறுகள் மோதலில் ஈடுபடும் போது பச்சை வண்ணத்துடன் கூடிய வெளிர் மஞ்சள் நிற ஒளி தோன்றும். அயனி நிலையில் உள்ள நைட்ரஜன் மூலக்கூறுகள் மோதலில் ஈடுபடும்போது, நீலம் அல்லது ஊதா - சிவப்பு வண்ண ஒளித்தோற்றம் தோன்றுகிறது.

2. காந்தத்தின் அடிப்படைப் பண்புகள்

சட்டகாந்தம் ஒன்றினை பின்வரும் கலைச் சொற்கள் மற்றும் பண்புகளின் அடிப்படையில் விவரிக்கலாம்.

(அ) காந்த இருமுனைதிருப்புத்திறன்

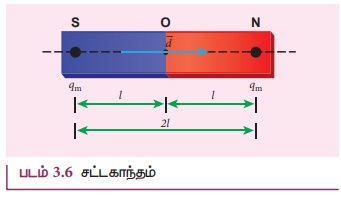
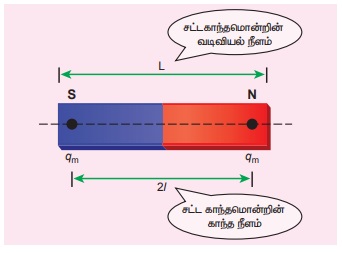
சட்ட காந்தம் ஒன்றை படம் 3.6 இல் உள்ளவாறு கருதுக. அதன் முனைவலிமையை q_m என்க. காந்தத்தின் வடிவியல் மையம் O விலிருந்து அதன் ஒருமுனையின் நீளம் l என்க. காந்தத்தின் முனைவலிமை மற்றும் காந்தநீளம் இவற்றின் பெருக்கற்பலன் ஆனது காந்த இருமுனை திருப்புத்திறன் என வரையறுக்கப்படுகிறது. இது ஒரு வெக்டர் அளவாகும். இதனை  என குறிப்பிடலாம்.

இங்கு  என்பது தென்முனையிலிருந்து வடமுனைவரை வரையப்பட்ட வெக்டரைக் குறிக்கிறது. அதன் எண்மதிப்பு 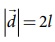 ஆகும்.

காந்த இருமுனை திருப்புத்திறனின் எண்மதிப்பு p_m =2q_m l

இதன் SI அலகு Am². காந்த இருமுனை திருப்புத்திறனின் திசை தென்முனையிலிருந்து வடமுனையை நோக்கி இருக்கும்.

(ஆ) காந்தப்புலம்

ஒரு காந்தத்தைச் சுற்றியுள்ள பகுதி அல்லது வெளியில், அக்காந்தத்தின் தாக்கம் வேறொரு காந்தத்தை வைக்கும் போது உணரப்பட்டால், அக்காந்தத்தைச் சுற்றியுள்ள பகுதி அல்லது வெளி காந்தப்புலமாகும். ஒரு புள்ளியில் வைக்கப்பட்டுள்ள ஓரலகு முனைவலிமை கொண்ட சட்டகாந்தம் உணரும் விசையே, அப்புள்ளியில் காந்தப்புலம்  என்று வரையறை செய்யப்படுகிறது.

இதன் அலகு NA^-1m^-1.

(இ) காந்தத்தின் வகைகள்

காந்தங்கள் இயற்கை காந்தங்கள் மற்றும் செயற்கை காந்தங்கள் என்று இருபெரும் பிரிவுகளாகவகைப்படுத்தப்பட்டுள்ளன. எடுத்துக்காட்டாக இரும்பு, கோபால்ட், நிக்கல் போன்றவை இயற்கை காந்தங்களாகும். இவ்வகை காந்தங்கள் மிகவும் வலிமை குறைந்தவை. அது மட்டுமில்லாமல் ஒழுங்கற்ற வடிவத்திலும் உள்ளன. நமக்குத் தேவையான வடிவம் மற்றும் வலிமையில் செயற்கை காந்தங்களை நாம் உருவாக்கலாம். செவ்வக வடிவிலோ அல்லது உருளை வடிவிலோ உருவாக்கப்பட்ட காந்தங்கள் சட்டகாந்தங்கள் என்று அழைக்கப்படுகின்றன.

காந்தத்தின் பண்புகள்

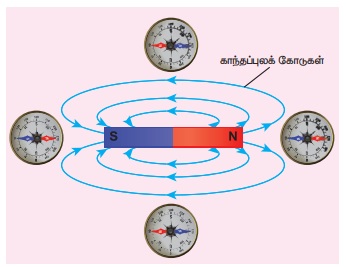
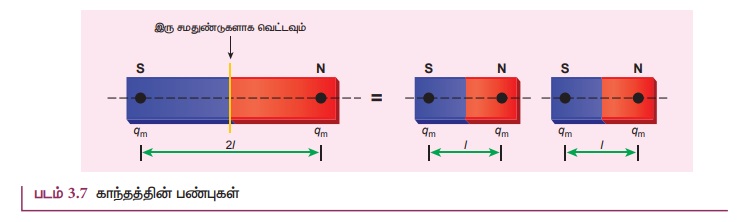
சட்டகாந்தத்தின் பண்புகள் பின்வருமாறு (படம் 3.7)

1. தடையின்றி தொங்கவிடப்பட்ட சட்டகாந்தம் எப்போதும் வட-தென் திசையை நோக்கியே நிற்கும்.

2. ஒரு காந்தம் மற்றொரு காந்தத்தை அல்லது காந்தப் பொருட்களை தன்னை நோக்கி ஈர்க்கும் அல்லது விலக்கும். இந்த ஈர்ப்பு அல்லது விலக்கு விசை சட்டகாந்தத்தின் முனைகளில் வலிமையாகக் காணப்படும். சட்டகாந்தம் ஒன்றினை இரும்புத்துருவல்களில் தோய்த்து எடுக்கும்போது, அதன் முனைகளில் இரும்புத்துருவல்கள் அதிகமாக ஒட்டிக் கொள்ளும்.

3. ஒரு காந்தம் துண்டுகளாக உடையும்போது, அதன் ஒவ்வொரு துண்டும் வடமுனை மற்றும் தென்முனை கொண்ட ஒரு காந்தம் போன்று செயல்படும்.

4. காந்தத்தின் இரண்டு முனைகளும் சமமுனைவலிமையைப் பெற்றிருக்கும்.

5. சட்டகாந்தம் ஒன்றின் மொத்த நீளம் அதன் வடிவியல் நீளம் (Geometric length) என்றும், காந்த முனைகளுக்கு இடையே உள்ள நீளம் காந்த நீளம் (Magnetic length) என்றும் அழைக்கப்படும். காந்தநீளம் எப்போதும் வடிவியல் நீளத்தை விடச் சற்றே குறைவாக இருக்கும். காந்த நீளத்திற்கும்வடிவியல் நீளத்திற்கும் உள்ள தகவு, 5/6 ஆகும்.

காந்த நீளம்/வடிவியல் நீளம் = 5/6 =0.833

எடுத்துக்காட்டு 3.2

சட்டகாந்தம் ஒன்றின் காந்தத்திருப்புத்திறன்  என்க. அதன் காந்தநீளம் d = 2l. மேலும் அதன் முனைவலிமை q_m ஆகும். அச்சட்டகாந்தத்தை

(அ) நீளவாக்கில் இரு சமதுண்டுகளாக வெட்டும் போது

(ஆ) நீளத்திற்கு குறுக்காக இரு சமதுண்டுகளாகவெட்டும் போது அதன் காந்தத்திருப்புத் திறனைக் கணக்கிடுக.

தீர்வு

(அ) சட்டகாந்தத்தை நீளவாக்கில் இருதுண்டுகளாக வெட்டும் போது, 

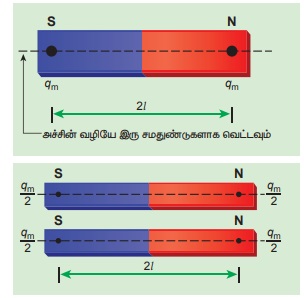
சட்டகாந்தத்தை நீளவாக்கில் அதன் அச்சின் வழியாக இருசமதுண்டுகளாக வெட்டும்போது,அதன் புதிய காந்தமுனை வலிமை 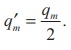 ஆனால் சட்டகாந்தத்தின் காந்த நீளம் மாறாது. எனவே, காந்தத்திருப்புத்திறன்.

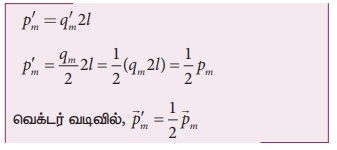
(ஆ) சட்டகாந்தத்தின் அச்சுக்கு செங்குத்தாக இரு சமதுண்டுகளாக வெட்டும் போது:

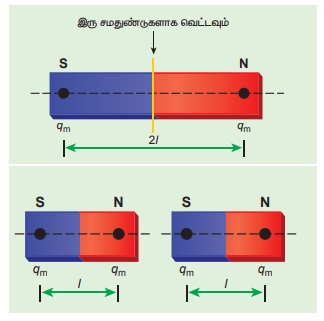
சட்டகாந்தத்தின் அச்சுக்கு செங்குத்தாக இரு சம் துண்டுகளாக வெட்டும்போது அதன் முனைவலிமையில் எவ்வித மாற்றமும் ஏற்படாது. ஆனால் காந்த நீளம் பாதியாகக் குறையும். எனவே காந்தத்திருப்புதிறன்

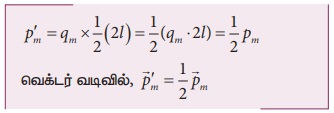
எடுத்துக்காட்டு 3.3

வடிவியல் நீளம் 12 cm கொண்ட சீரான சட்ட காந்தம் ஒன்றின் காந்த நீளத்தைக் கண்டறிந்து, காந்த முனைகள் அமைந்திருக்கும் இடத்தைக் குறித்துக் காட்டுக.

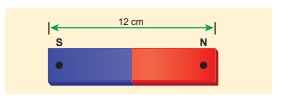
தீர்வு

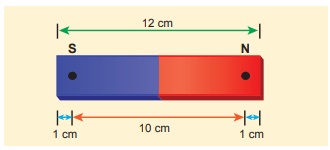
காந்தத்தில் வடிவியல் நீளம் = 12 cm

காந்த நீளம் = 5/6  x(வடிவியல் நீளம்)

= 5/6 x 12 = 10 cm

பின்வரும் படத்தில் காட்டப்பட்டுள்ள புள்ளிகள் காந்தத்தின் முனைகளைக் குறிக்கின்றன.

குறிப்பு

(i) முனைவலிமை ஒரு ஸ்கேலர் அளவாகும். அதன் பரிமாணம்[M°LT°A] ஆகும். இதன் SI அலகு NT^-1 (நியூட்டன் / டெஸ்லா ) அல்லது A m (ஆம்பியர் - மீட்டர்).

(ii) நிலைமின்னியலில் உள்ள நேர்க்குறி மற்றும் எதிர்க்குறி மின்துகள்களைப் போன்றே, காந்தப்புலத்தில் உள்ள ஒரு காந்தத்தின் வடமுனை, காந்தப்புலத்தின் திசையிலேயே விசையை உணரும். அதே நேரத்தில் காந்தத்தின் தென்முனை காந்தப்புலத்தின் திசைக்கு எதிர்த்திசையில் விசையை உணரும்.

(iii) முனைவலிமையானது, காந்தப்பொருளின் தன்மை, அதன் குறுக்கு-வெட்டுப்பரப்பு மற்றும் எந்த அளவிற்கு அப்பொருள் காந்தமாக்கப்பட்டுள்ளது என்பவற்றைச் சார்ந்தது.

(iv) காந்தம் ஒன்றினை நீளவாக்கில் இரு சமதுண்டுகளாக வெட்டினால், அதன் முனைவலிமை பாதியாகக் குறையும்.

(v) காந்தம் ஒன்றின் நீளத்திற்கு செங்குத்தாக அதனை இருசமதுண்டுகளாக வெட்டினால், அதன் முனைவலிமையில் எவ்வித மாற்றமும் ஏற்படாது.

(vi) காந்தம் ஒன்றினை இருதுண்டுகளாக வெட்டி அதிலிருந்து தனித்த வடமுனையையோ தென்முனையையோ பெறமுடியாது. மாறாக நமக்கு இரண்டு தனித்தனியான காந்தங்கள் கிடைக்கும் வேறு வகையில் கூறுவோமாயின், இயற்கையில் தனித்த வடமுனை அல்லது தனித்த தென்முனை என்ற ஒன்று இல்லை.

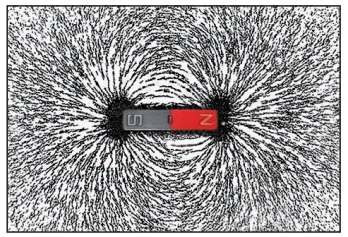
காந்தப்புலக் கோடுகள்

1. காந்தப் புலக்கோடுகள் தொடர்ச்சியான மூடப்பட்டவளைகோடுகளாகும். காந்தப்புலக்கோடுகளின் திசை காந்தத்திற்கு வெளியே வடமுனையிலிருந்து தென்முனை நோக்கியும் காந்தத்திற்கு உள்ளே தென்முனையிலிருந்துவடமுனை நோக்கியும் இருக்கும்.

2. மூடப்பட்ட வளைகோட்டின் எந்த ஒரு புள்ளியிலும் உள்ள காந்தப்புலத்தின் திசையை, அப்புள்ளியில் உள்ள காந்தப்புலக் கோட்டிற்கு வரையப்படும்தொடுகோட்டின் திசையிலிருந்து அறியலாம்.

3. காந்தப்புலக்கோடுகள் எப்போதும் ஒன்றைஒன்று வெட்டாது. அவ்வாறு வெட்டிக்கொண்டால் திசைகாட்டும் கருவியில் உள்ள காந்த ஊசி ஒரே புள்ளியில் இரண்டு வெவ்வேறு திசைகளைக் காட்டும். இது நடைமுறையில் சாத்தியமற்றது.

4. காந்தப்புலத்தின் வலிமைக்குத் தக்கவாறு, காந்தப்புலக்கோடுகள் அமைந்திருக்கும். அதாவது வலிமையான காந்தப்புலத்திற்கு கோடுகள் மிக நெருக்கமாகவும், வலிமை குறைந்த காந்தப்புலத்திற்கு இடைவெளி விட்டும் காணப்படும்.

(ஈ) காந்தப்பாயம்

குறிப்பிட்ட பரப்பிற்கு செங்குத்தாக செல்லும் காந்தப்புலக் கோடுகளின் எண்ணிக்கைக்கு காந்தப்பாயம் ppppppp என்று பெயர். கணிதவியலின்படி, ஒரு சீரான காந்தப்புலத்தில் A பரப்பு வழியாகச் செல்லும் காந்தப்பாயத்தை பின்வருமாறு வரையறுக்கலாம்.

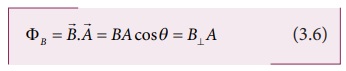
இங்கு θ என்பது  மற்றும்  வெக்டர்களுக்கு இடையே உள்ள கோணமாகும். இது படம் 3.8 இல் காட்டப்பட்டுள்ளது.

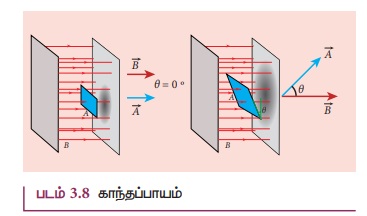
சிறப்பு நேர்வுகள்

(அ) பரப்பிற்கு செங்குத்தாக  உள்ள போது, அதாவதுθ = 0° எனில், காந்தப்பாயம் Ø_B = BA (பெருமம்).

(ஆ)பரப்பிற்கு இணையாக   உள்ளபோது, அதாவதுθ = 90° எனில், காந்தப்பாயம் Ø_B = 0.

சீரற்ற காந்தப்புலம் உள்ள பரப்பிற்கு சமன்பாடு (3.6) ஐ. பின்வருமாறு எழுதலாம்.

(இங்கு பரப்பு முழுவதும் தொகையிடல் (Integral) செய்யப்படுகிறது).

காந்தப்பாயம் ஒரு ஸ்கேலர் அளவாகும். இதன் SI அலகு வெபர் (weber). இதனை Wb என குறிப்பிட வேண்டும். காந்தப்பாயத்தின் பரிமாண வாய்ப்பாடு ML²T^-2A^-1. இதன் CGS அலகு மேக்ஸ்வெல் ஆகும்.

1 வெபர் = 10⁸ மேக்ஸ்வெல்

காந்தப்புலக் கோடுகளுக்கு செங்குத்தாக உள்ள ஓரலகுப் பரப்பின் வழியாகச் செல்லும் காந்தப்புலக் கோடுகளின் எண்ணிக்கையே காந்தப்பாய அடர்த்தியாகும்.

இதன் அலகு Wb m^-2 அல்லது டெஸ்லா (T).

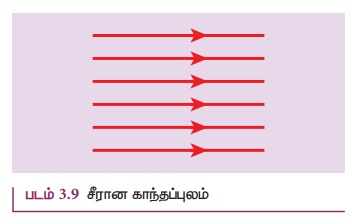
(உ) சீரான மற்றும் சீரற்ற காந்தப்புலம்

சீரான காந்தப்புலம் கொடுக்கப்பட்ட பகுதியில் உள்ள அனைத்து புள்ளிகளிலும் காந்தப்புலத்தின் எண்மதிப்பு மற்றும் திசை ஆகியவை மாறாமல் இருந்தால், அதனை சீரான காந்தப்புலம் என்று அழைக்கலாம். எடுத்துக்காட்டாக, குறிப்பிட்ட சிறிய பகுதியில் புவியின் காந்தப்புலம் சீரான காந்தப்புலமாகும்.

உதாரணத்திற்கு உங்கள் பள்ளியின் நிலப்பரப்பு முழுவதும் புவிகாந்தப்புலம் ஒரு மாறாத மதிப்பினைப் பெற்றிருக்கும்!

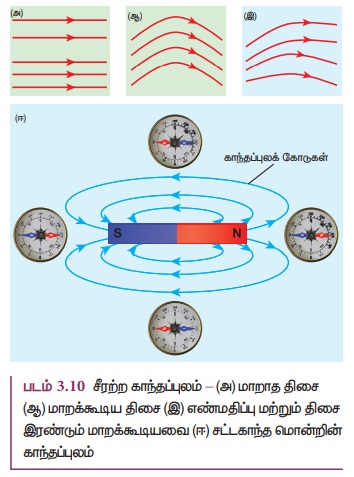
சீரற்ற காந்தப்புலம்

கொடுக்கப்பட்ட பகுதியில் உள்ள அனைத்து புள்ளிகளிலும் காந்தப்புலத்தின் எண்மதிப்பு அல்லது திசை அல்லது இரண்டுமே மாற்றமடைந்தால், அக்காந்தப்புலத்தை சீரற்ற காந்தப்புலம் என்று அழைக்கலாம்.

எடுத்துக்காட்டு: சட்டகாந்தம் ஒன்றின் காந்தப்புலம்.

எடுத்துக்காட்டு 3.4

பின்வரும் படத்தில் காட்டப்பட்டுள்ள காந்த இருமுனை (சட்ட காந்தம்) வைக்கப்பட்டுள்ள பரப்பிலிருந்து வெளிவரும் காந்தபாயத்தைக் கணக்கிடுக.

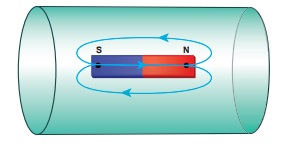
தீர்வு

காந்த இருமுனை வைக்கப்பட்டுள்ள மூடப்பட்டப்பரப்பிலிருந்து (S) வெளிவரும் மொத்த காந்தப்பாயம் சுழியாகும். எனவே,

இங்கு மூடப்பட்ட பரப்பு S முழுவதும் தொகையிடல் செய்யப்படுகிறது. இதன் மதிப்பு எப்போதும் சுழியாகும் ஏனெனில் தனித்த காந்தமுனை (காந்த ஒருமுனை) என்ற ஒன்று இல்லை.

இது நிலைமின்னியலில் கூறப்பட்டுள்ள காஸ்விதியினை ஒத்துள்ளது (அலகு 1 ஐப் பார்க்கவும்).