12 வது இயற்பியல் : அலகு 3 : காந்தவியல் மற்றும் மின்னோட்டத்தின் காந்தவிளைவுகள்
சீரான காந்தப்புலத்தில் உள்ள சட்டகாந்தத்தின் மீது செயல்படும் திருப்புவிசை
சீரான காந்தப்புலத்தில்
உள்ள சட்டகாந்தத்தின் மீது செயல்படும் திருப்புவிசை
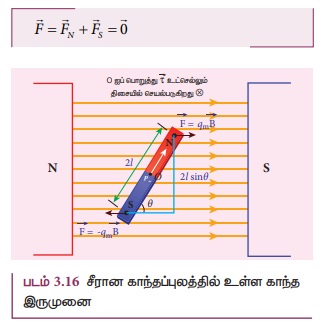
2l நீளமும் qm முனைவலிமையும் கொண்ட
காந்தமொன்று![]() என்ற சீரான காந்தப்புலத்தில் படம் 3.16 இல் காட்டியுள்ளவாறுவைக்கப்பட்டுள்ளது.
ஒவ்வொரு காந்தமுனையும் எதிரெதிர் திசையில் செயல்படும் qm B என்ற விசையை
உணர்கின்றன. எனவே காந்தத்தின் மீது செயல்படும் தொகுபயன்விசை சுழியாகும். எவ்விதமான
இடப்பெயர்ச்சி இயக்கமும் இங்கு ஏற்படாது. இவ்விரண்டு விசைகளும்காந்தத்தின் மையத்தைப்
பொறுத்து ஒரு இரட்டையை உருவாக்கும். இவ்விரட்டை காந்தத்தைச் சுழற்றி, காந்தப்புலம்
என்ற சீரான காந்தப்புலத்தில் படம் 3.16 இல் காட்டியுள்ளவாறுவைக்கப்பட்டுள்ளது.
ஒவ்வொரு காந்தமுனையும் எதிரெதிர் திசையில் செயல்படும் qm B என்ற விசையை
உணர்கின்றன. எனவே காந்தத்தின் மீது செயல்படும் தொகுபயன்விசை சுழியாகும். எவ்விதமான
இடப்பெயர்ச்சி இயக்கமும் இங்கு ஏற்படாது. இவ்விரண்டு விசைகளும்காந்தத்தின் மையத்தைப்
பொறுத்து ஒரு இரட்டையை உருவாக்கும். இவ்விரட்டை காந்தத்தைச் சுழற்றி, காந்தப்புலம் ![]() இன் திசையிலேயே அதனை ஒருங்கமைக்க முயற்சிக்கும்.
இன் திசையிலேயே அதனை ஒருங்கமைக்க முயற்சிக்கும்.

சமன்பாடு (3.23) மற்றும் (3.24) ஐ ஒன்றுடன்
ஒன்று கூட்டும்போது காந்த இருமுனையின் மீது செயல்படும் தொகுபயன்விசை
புள்ளி O வைப்பொறுத்து வட மற்றும் தென்முனை
உணரும் திருப்புவிசை
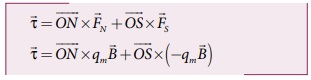
மொத்தத் திருப்புவிசை, தாளினை நோக்கி செயல்படுவதை
வலதுகை திருகு விதியினைப் பயன்படுத்தி அறியலாம்.
இங்கு எண்மதிப்புகள் ![]() =
=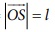 மற்றும்
மற்றும் 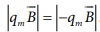 எனவே, புள்ளி O வைப் பொருத்து மொத்தத் திருப்புவிசையின் எண்மதிப்பு
எனவே, புள்ளி O வைப் பொருத்து மொத்தத் திருப்புவிசையின் எண்மதிப்பு
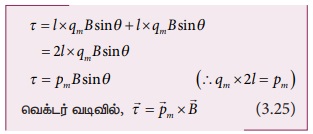
உங்களுக்குத் தெரியுமா?
(அ) புவி ஒரு சீரற்ற காந்தப்புலத்தைப்பெற்றிருந்தாலும், உங்கள்
ஆய்வுக்கூடத்தில் தடையின்றிதொங்கவிடப்பட்டுள்ள சட்டகாந்தம் இடப்பெயர்ச்சி இயக்கத்தை
மேற்கொள்ளாமல், சுழற்சி இயக்கத்தை மட்டுமே (திருப்புவிசை) மேற்கொள்கிறது ஏன்?
ஏனெனில், ஒரு குறிப்பிட்ட பகுதிக்குள் (உங்கள் ஆய்வுக் கூடத்திற்குள்)
புவியின் காந்தப்புலம் சீரானது.
(ஆ) ஒரு சீரற்ற காந்தப்புலத்தில், சட்டகாந்தமொன்று தடையின்றி தொங்கவிடப்பட்டுள்ள
போது என்ன நிகழும்?
அச்சட்டகாந்தம், இடப்பெயர்ச்சி இயக்கம் (தொகுபயன் விசை மூலமாக)
மற்றும் சுழற்சி இயக்கம் (திருப்புவிசை மூலமாக) இவ்விரண்டையும் உணரும்.
எடுத்துக்காட்டு
3.7
புறகாந்தப்புலம் ஒன்றில் உள்ள காந்த இருமுனையைக்கருதுக.
புறகாந்தப்புலம் செயல்படும்போது காந்த இருமுனை இரண்டு வழிகளில் மட்டுமே ஒருங்கமையும்.
அதாவது ஒன்று புறகாந்தப்புலத்தின் திசையில் (புறகாந்தப்புலத்திற்குஇணையாக) மற்றொன்று
புறகாந்தப்புலத்தின் திசைக்கு எதிர்த்திசையில் இவ்விரண்டு நிகழ்வுகளிலும் தோன்றும்
ஆற்றலைக் கணக்கிட்டு அதற்கான வரைபடங்களை வரைக.
தீர்வு
சட்டகாந்தத்தின் இருமுனைதிருப்புத்திறன் ![]() என்க. புறகாந்தப்புலம் செயல்படாத நிலையில் எவ்வித ஒருங்கமைவும் ஏற்படாது.
எனவே ஆற்ற ல் U = 0.
என்க. புறகாந்தப்புலம் செயல்படாத நிலையில் எவ்வித ஒருங்கமைவும் ஏற்படாது.
எனவே ஆற்ற ல் U = 0.
புறகாந்தப்புலம் செயல்பட்ட உடன், காந்த இருமுனை
புறகாந்தப்புலத்தின் திசையில் (θ = 0°) ஒருங்கமையும்போது அதன்
ஆற்றல்
Uஇணை = Uசிறுமம்
=-pmBcos 0°
Uஇணை = -pmB
ஏனெனில் cos 0° = 1
அவ்வாறு இல்லையெனில், காந்த இருமுனை புறகாந்தப்புலத்தின்
திசைக்கு எதிர்த்திசையில் (θ= 180°) ஒருங்கமையும் போது அதன்
ஆற்றல்
Uஎதிர்-இணை = Uபெருமம்
=-pmBcos180°
= Uஎதிர்-இணை= pmB
ஏனெனில் cos 180° = -1
சீரான காந்தப்புலத்தில் உள்ள சட்டகாந்தமொன்றின் நிலையாற்றல் (Potential energy)
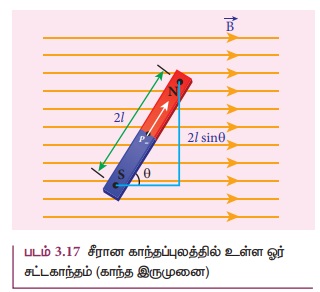
இருமுனை திருப்புத்திறன் ![]() கொண்ட
சட்டகாந்தமொன்று (காந்த இருமுனை), சீரான காந்தப்புலம்
கொண்ட
சட்டகாந்தமொன்று (காந்த இருமுனை), சீரான காந்தப்புலம் ![]() உடன் θ கோணத்தில்
படம் 3.17 இல் காட்டியுள்ளவாறு வைக்கப்பட்டுள்ளது. இருமுனையின் மீது செயல்படும் திருப்புவிசையின்
எண்மதிப்பு
உடன் θ கோணத்தில்
படம் 3.17 இல் காட்டியுள்ளவாறு வைக்கப்பட்டுள்ளது. இருமுனையின் மீது செயல்படும் திருப்புவிசையின்
எண்மதிப்பு

![]() க்கு எதிராக மாறாத கோண திசைவேகத்தில்
dθ என்ற
சிறிய கோண இடப்பெயர்ச்சிக்கு காந்தஇருமுனை (சட்டகாந்தம்) சுழற்றப்படுகிறது என்க. இந்த
சிறிய கோண இடப்பெயர்ச்சிக்கு, புறத்திருப்புவிசையால்
க்கு எதிராக மாறாத கோண திசைவேகத்தில்
dθ என்ற
சிறிய கோண இடப்பெயர்ச்சிக்கு காந்தஇருமுனை (சட்டகாந்தம்) சுழற்றப்படுகிறது என்க. இந்த
சிறிய கோண இடப்பெயர்ச்சிக்கு, புறத்திருப்புவிசையால் ![]() செய்யப்பட வேலை
செய்யப்பட வேலை

இங்கு சட்டகாந்தம் மாறாத கோணத் திசைவேகத்தில்
சுழலுகிறது.
இதிலிருந்து, 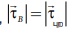
dW = pm Bsinθ dθ
காந்த இருமுனையைθ’ லிருந்து
θ வரை
சுழற்றுவதற்கு செய்யப்பட்ட மொத்த வேலை
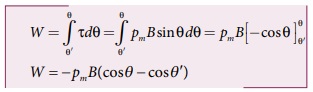
θ லிருந்து θ வரை
சுழற்றுவதற்கு செய்யப்பட்ட இந்த வேலை, கோணத்தில் உள்ள சட்டகாந்தத்தில் நிலை ஆற்றலாக
சேமித்துவைக்கப்படுகிறது. மேலும் இதனை பின்வருமாறு எழுதலாம்.
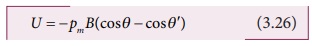
உண்மையில் θ மற்றும்θ என்ற
இருவேறு கோணநிலைகளுக்கு இடையே உள்ள நிலையாற்றல் வேறுபாட்டைத்தான் சமன்பாடு (3.26) கொடுக்கிறது.
θ' =
900 என்ற குறிப்புப்புள்ளியை நாம் கருதும்போது மேலே உள்ள சமன்பாட்டின் இரண்டாம்
பகுதி சுழியாகும். எனவே சமன்பாடு (3.26) ஐ பின்வ ருமாறு எழுதலாம்.

சீரான காந்தப்புலத்தில் உள்ள சட்ட காந்தமொன்றில்
சேமித்து வைக்கப்பட்டுள்ள ஆற்றல்

நேர்வு 1
(i) θ =
0°, எனில்
U=-pmB (cos0°) =-pmB
(ii) θ =
180°, எனில்
U =-pmB (cos180°) = pm
B
மேற்கண்ட இரண்டு முடிவுகளிலிருந்து நாம் அறிவது என்னவென்றால், சட்டகாந்தம் புறகாந்தப்புலத்தின் திசையில் ஒருங்கமையும்போது அதன் நிலையாற்றல் சிறுமமாகவும், புறகாந்தப்புலத்தின் திசைக்கு எதிர்த்திசையில் ஒருங்கமையும் போது அதன் நிலையாற்றல் பெருமமாகவும் இருக்கும்.