காந்தவியல் மற்றும் மின்னோட்டத்தின் காந்தவிளைவுகள்: நெடுவினாக்கள்

III. நெடுவினாக்கள்

1. புவி காந்தப்புலத்தைப் பற்றி விரிவாக விளக்கவும். 

• வில்லியம் கில்பர்ட் என்ற அறிஞர், புவி ஒரு மிகப் பெரிய ஆற்றல் வாய்ந்த சட்ட காந்தம் என்ற கொள்கையை முன் மொழிந்தார்.

• புவியின் உள்ளே உள்ள மிக உயர்ந்த வெப்ப நிலையில், அக்காந்தம் அதன் காந்தத் தன்மையை இழந்துவிடும். 

• சூரியனிடமிருந்து வரும் வெப்பக் கதிர்கள் தான் புவியின் காந்தப்புலத்திற்குக் காரணம் என்று கோவர் முன் மொழிந்தார்.

• புவியின் காந்தப் புலமைப் பற்றி படிக்கும் இயற்பியலின் பிரிவிற்கு புவி காந்தவியல் அல்லது நிலக் காந்தவியல் என்று பெயர்.

• காந்தப்புலத்தை குறிப்பிடுவதற்கு மூன்று அளவுகள் தேவைப்படுகின்றன. அவை 

i) காந்த ஒதுக்கம் 

ii) காந்தச் செறிவு 

iii) புவிக்காந்தப்புலத்தின் கிடைத்தளக் கூறு. 

BE − புவியின் காந்தப்புலம் 

BH −கிடைத்தளக் கூறு 

Bv − செங்குத்துக் கூறு 

கிடைத்தளக்கூறு BH = BE Cos I

செங்குத்துக் கூறு BV = BE Sin I

tan I = BV / BH

i) காந்த நடுவரைக் கோட்டில் BH = BE [I = 0°]

Bv = 0 

ii) காந்த துருவங்களில் BE = 0 [I = 90°]

 Bv = BE 

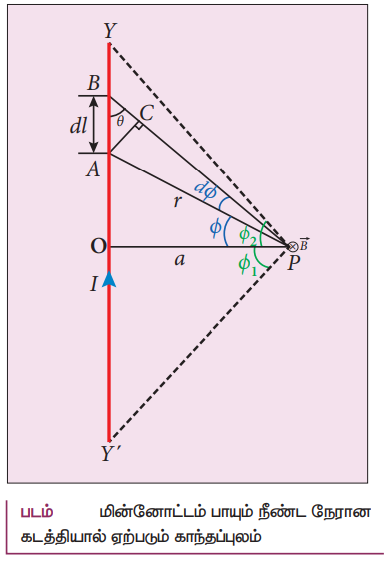
2. பயட்-சாவர்ட் விதி உதவியுடன் மின்னோட்டம் பாயும் முடிவிலா நீளம் கொண்ட நேர்க்கடத்தியால் ஒரு புள்ளியில் ஏற்படும் காந்தப்புலத்துக்கான கோவையைப் பெறுக. 

• NM என்ற நீண்ட நேரான கடத்தியில் I மின்னோட்டம் பாய்கிறது என கருதுக. 

• 𝓁 நீளமுள்ள கடத்தியில் உள்ள d𝓁 நீளமுள்ள சிறு கூறு ஒன்றினை கருதுக. 

• O புள்ளியிலிருந்து 'a' தொலைவில் உள்ள P என்ற புள்ளியைக் கருதுக. 

• பயோட்−சாவர்ட் விதிப்படி

• காந்தப் புலத்தின் திசை தாளின் தளத்திற்குச் செங்குத்தாக தாளுக்கு உள்ளே செல்லும் வகையில் உள்ளது. 

• படத்தில் உள்ளபடி முக்கோணம் PAO−வில்

3. பயோட்−சாவர்ட் விதி உதவியுடன் மின்னோட்டம் பாயும் வட்டவடிவக் கம்பிச் சுருளின் அச்சில் ஒரு புள்ளியில் ஏற்படும் காந்தப்புலத்துக்கான கோவையைப் பெறுக. 

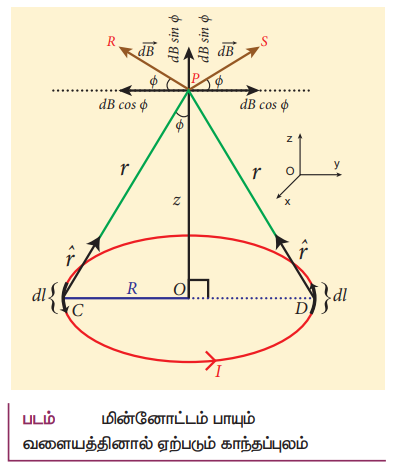
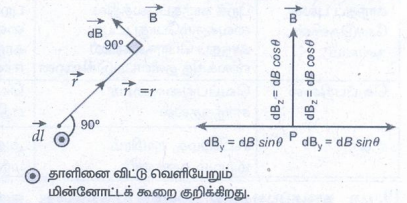
பயோட் −சாவர்ட் விதியைக் கொண்டு மின்னோட்டம் பாயும் வளையத்தின் அச்சுக்கோட்டில் ஏற்படும் காந்தப் புலத்தைக் காணல் 

• R ஆரமுடைய மின்னோட்டம் பாயும் வளையம் ஒன்றைக் கருதுக. 

• வளையத்தின் மையம் O விலிருந்து Z தொலைவில் உள்ள அதன் அச்சின் மீது அமைந்துள்ள புள்ளி P யைக் கருதுக. 

• C மற்றும் D புள்ளிகளில் உள்ள நீளமுடைய இருநீளக் கூறுகளைக் கருதுக. 

• மின்னோட்டக் கூறு (I ) மற்றும் P புள்ளியை இணைக்கும் வெக்டரை என்க.

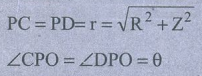
∠ CPO = ∠ DPO = θ

• பயோட் − சாவர்ட் விதியின் படி

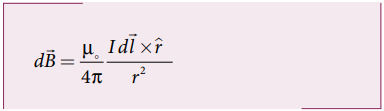
• இரண்டு கூறுகளாகப் பிரிக்கலாம்

dB sin θ − y திசையில்

dB cos θ − z திசையில்

• கிடைத்தளக் கூறுகள் ஒன்றை ஒன்று சமன் செய்து கொள்ளும். 

• ஐ வளையத்தைச் சுற்றி தொகைப்படுத்தும் போது, ஒரு கூம்பினை உருவாக்கும். 

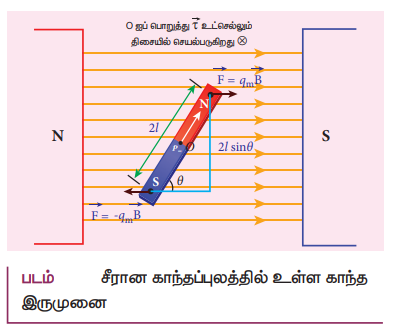
4. சீரான காந்தப்புலத்திலுள்ள காந்த ஊசி ஒன்றின் மீது செயல்படும் திருப்பு விசைக்கான கோவையைப் பெறுக. 

• 2l நீளம் கொண்ட ஒரு காந்தத்தை கருதுக. 

• முனைவலிமை −qm 

• ஒவ்வொரு காந்த முனையும் எதிரெதிர் திசையில் செயல்படும் விசை qmB 

• தொகுபயன் விசை சுழியாகும். 

• காந்தத்தின் மையத்தைப் பொறுத்து, ஒரு இரட்டையை உருவாக்கும்.

• திருப்பு விசை

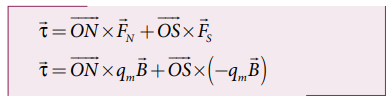
• மொத்த திருப்புவிசை, தாளினை நோக்கி செயல்படுவதை வலதுகை திருகு விதியின் மூலம் அறியலாம்

5. சட்ட காந்தமொன்றின் அச்சுக்கோட்டில் ஏதேனும் ஒரு புள்ளியில் ஏற்படும் காந்தப்புலத்துக்கான கோவையைப் பெறுக. 

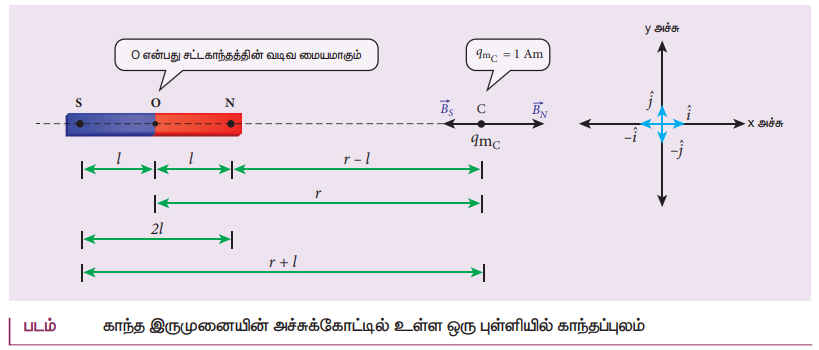
• NS என்ற சட்ட காந்தம் ஒன்றைக் கருதுக. 

• N− வடமுனை, S − தென்முனை 

• qm −முனை வலிமை 

• தொலைவு – 2l 

• r என்ற தொலைவில் அச்சுக்கோட்டில் அமைந்த C என்ற புள்ளியைக் காண்க. 

• காந்தவியலின் கூலூம் விதியைப் பயன்படுத்தி

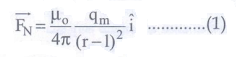
• r − 1 → என்ற சட்டகாந்தத்தின் வடமுனை மற்றும் C புள்ளியில் உள்ள ஓரலகு வடமுனைக்கும் இடையே உள்ள தொலைவு 

• ஈர்ப்பு விசை

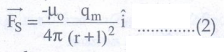
• r + 1 → சட்டகாந்தத்தின் தென்முனைக்கும், C புள்ளியில் உள்ள ஓரலகு வடமுனைக்கும் இடையேயான தொலைவு 

• C புள்ளியில் தொகுபயன் விசை

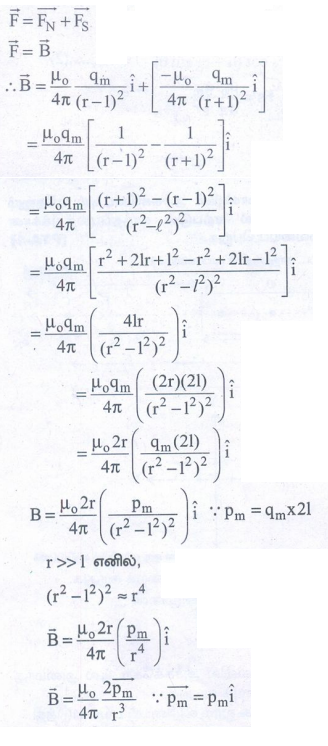
6. சட்ட காந்தமொன்றின் நடுவரைக்கோட்டில் ஏதேனும் ஒரு புள்ளியில் ஏற்படும் காந்தப்புலத்துக்கான கோவையைப் பெறுக. 

• NS என்ற சட்ட காந்தம் ஒன்றைக் கருதுக. 

• N−வடமுனை S− தென்முனை

• முனை வலிமை−qm

• தொலைவு 2l

• r என்ற தொலைவில் அதன் நடுவரைக் கோட்டில் அமைந்த C என்ற புள்ளியைக் காண்க. 

• விலக்கு விசை 

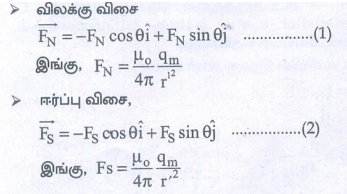
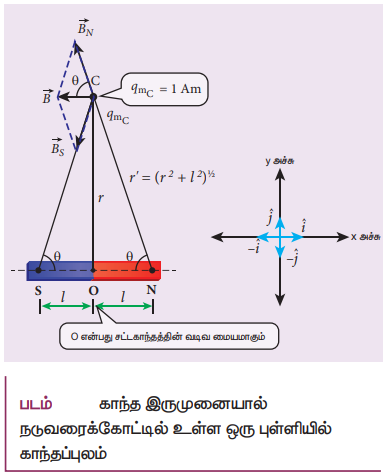
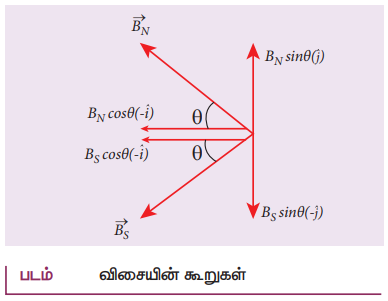
தொகுபயன் விசை C புள்ளியில் 

7. ஆம்பியரின் சுற்றுவிதியைக் கொண்டு, மின்னோட்டம் பாயும் நீண்ட நேரான கடத்தியினால் ஏற்படும் காந்தப்புலத்தைக் காண்க. 

• முடிவிலா நீளம் கொண்ட I மின்னோட்டம் பாயும் நேரான கடத்தி ஒன்றைக் கருதுக. 

• நுண்ணளவில் பார்க்கும் போது கம்பி உருளை வடிவில் உள்ளது. 

• அச்சினைப் பொறுத்து சமச்சீராக உள்ளது. 

• கடத்தியின் மையத்திலிருந்து r தொலைவில் வட்ட வடிவிலான ஆம்பியரின் வளையத்தை உருவாக்க வேண்டும். 

• ஆம்பியரின் விதிப்படி

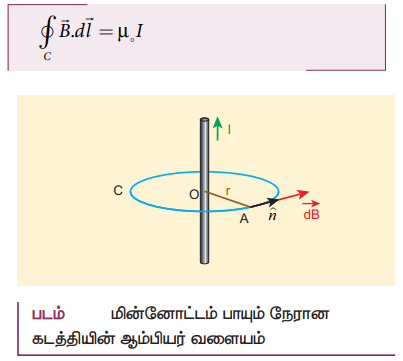
• என்பது ஆம்பியரின் வளையம் வழியேச் செல்லும் வரிக்கூறாகும். 

• காந்தப்புல வெக்டருக்கும் வரிக்கூறுக்கும் இடையே உள்ள கோணம் சுழியாகும்.

• B எண் மதிப்பு மாறாமலிருக்கும்.

• ஆம்பியர் வளையத்தின் சுற்றளவு = 2πr

• தொடுகோட்டின் வழியே ஆம்பியரின் வளையத்திற்குச் செல்லும் ஓரலகு வெக்டராகும்.

8. சைக்ளோட்ரான் இயங்கும் முறையை விரிவாக விளக்கவும். 

• மின்துகள்களை முடுக்குவித்து, அவை பெறும் இயக்க ஆற்றலை பயன்படுத்த உதவும் கருவி. 

• உயர் ஆற்றல் முடுக்குவிப்பான் என்றும் அழைக்கலாம்.

தத்துவம்: மின்துகள், காந்தப்புலத்திற்கு செங்குத்தாக செல்லும் போது, அது லாரன்ஸ் விசையை உணரும். 

கட்டமைப்பு: 

• அரைவட்ட உலோகக் கொள்கலன்கள் D−க்கள் நடுவே மின்துகள்கள் செலுத்தப்படுகின்றன. 

• மின்காந்தங்களினால் கட்டுப்படுத்தப்பட்ட சீரான காந்தப்புலத்தினால் சூழப்பட்டுள்ளது. 

• D−க்களின் தளத்திற்கு செங்குத்தாக காந்தப்புலத்தின் திசை உள்ளது. 

• D−க்களின் இடைவெளியின் நடுவே 'S' உள்ளது. 

• உயர் அதிர்வெண் கொண்ட மாறுதிசை மின்னழுத்த வேறுபாட்டு மூலம் இணைக்கப்பட்டுள்ளது. 

வேலை செய்யும் முறை:

• அயனி மூலம் S, நேர் மின்னோட்டம் கொண்ட அயனி ஒன்றை உமிழ்கிறது. எதிர் மின்னழுத்தம் கொண்ட D−யினால் அந்த அயனி முடுக்கப்படுகிறது.

• அயனி வட்டப்பாதையை மேற்கொள்ளும் 

• D−1 இல் அரை வட்டப்பாதையை அயனி நிறைவு செய்த உடன், D−க்களுக்கு நடுவே உள்ள இடைவெளியை அடையும்.

• அந்நேரத்தில் D−க்களின் துருவம் மாற்றப்படும். எனவே D−2 ஐ நோக்கி அதிக திசைவேகத்துடன் முடுக்கப்படும்.

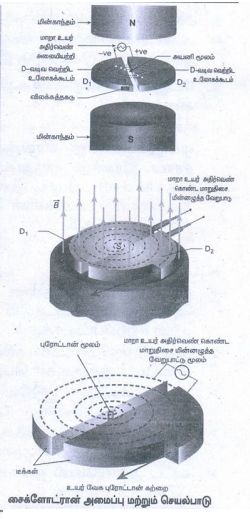
• அயனி ஒரு வட்டப்பாதையை நிறைவு செய்யும் 

• மையநோக்கு விசையை லாரன்ஸ் விசை கொடுக்கிறது.

• சுருள்வட்டப் பாதையின் ஆரம் அதிகரித்தால் திசைவேகமும் அதிகரிக்கும். 

• மின் துகளானது D−க்களின் ஓரத்தை நெருங்கும் போது, விலக்கத்தகட்டின் உதவியுடன் அதனை வெளியேற்றி இலக்கின் மீது மோதச் செய்யலாம்.

• ஒத்திசைவு நிபந்தனை

வரம்புகள்: 

• அயனியின் வேகம் வரம்புக்குட்பட்டது. 

• எலக்ட்ரானை மற்றும் மின்னூட்ட மற்ற துகள்களை முடுக்குவிக்க இயலாது. 

9. டேஞ்சன்ட் விதியைக்கூறி, அதனை விரிவாக விளக்கவும். 

டேஞ்சன்ட் விதி

ஒன்றுக்கொன்று செங்குத்தாகக் செயல்படும் சீரான இரண்டு காந்தப்புலங்களுக்கு நடுவே தொங்கவிடப்பட்டுள்ள காந்த ஊசி, இவ்விரண்டு புலங்களின் தொகுபயன் புலத்தின் திசையில் நிற்கும்.

B = BH tan θ ……………………..(1)

கட்டமைப்பு 

• வட்டவடிவ பித்தளை அல்லது மரத்தால் செய்யப்பட்ட சட்டத்தின் மீது தாமிரக் கம்பிச் சுருள் சுற்றப்பட்டிருக்கும். 

• கிடைத்தள மேடையை சரிசெய்ய கிடைமட்டத்திருகுகள் பெற்றுள்ளது. 

• சுழல் மேடைக்கு நடுவே காந்த ஊசிப் பெட்டி பொருத்தப்பட்டுள்ளது. 

• மெல்லிய அலுமினியக்குறிமுள் ஒன்று காந்த ஊசிக்கு செங்குத்தாக அமைக்கப்பட்டுள்ளது. 

• வட்ட அளவுகோல் நான்கு கால் வட்டங்களாகப் பிரிக்கப்பட்டுள்ளது.

கொள்கை 

• ஒன்றுக்கொன்று செங்குத்தாகச் செயல்படும் இரண்டு காந்தப்புலங்கள் உள்ளன. 

• மின்னோட்டம் பாயும் கம்பிச் சுருளின் தளத்திற்குச் செங்குத்தாக செயல்படும் காந்தப்புலம் 

• புவி காந்தப்புலத்தின் கிடைத்தளக் கம்பிச் சுருளின் வழியே மின்னோட்டம் பாய்வதால் அதன் மையத்தில் தோன்றும் காந்தப்புலம் 

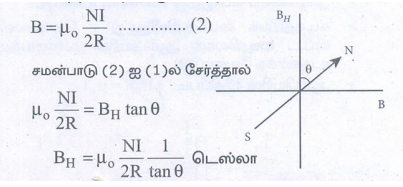
10. காந்தப்புலத்தில் உள்ள மின்னோட்டச்சுற்றின் மீது செயல்படும் திருப்புவிசைக்கான கோவையை வருவி.

மின்னோட்டச் சுற்றின் மீது செயல்படும் திருப்பு விசை

காந்தப்புலத்திலுள்ள மின்னோட்டம் பாயும் கடத்தியின் மீது செயல்படும் விசை, விசைப்பொறி (motor) ஒன்றின் செயல்பாட்டிற்கு அடிப்படையாக அமைகிறது.

காந்தப்புலத்திலுள்ள மின்னோட்டச் சுற்றின் மீது செயல்படும் திருப்பு விசை

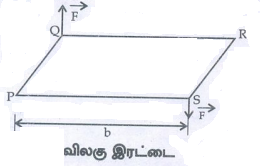
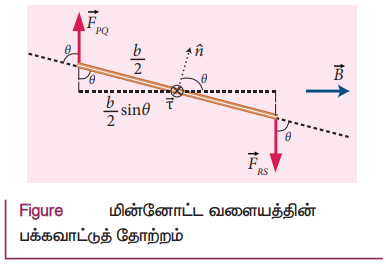
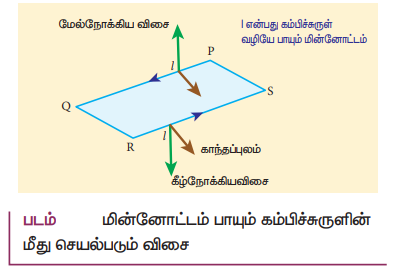
சீரான காந்தப்புலம் ல் வைக்கப்பட்டுள்ள மின்னோட்டம் I பாயும் செவ்வகச் சுருள் PQRSஐக் கருதுக. சுருளின் நீளம் மற்றும் அகலம் முறையே a மற்றும் b என்க. படம்தில் காட்டியுள்ளபடி சுருளின் தளத்திற்கு செங்குத்தாக வரையப்பட்ட ஓரலகு வெக்டர் n^ காந்தப்புலத்திற்கு θ கோணத்தில் உள்ளது.

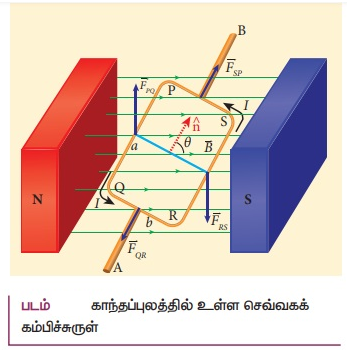
மின்னோட்டம் தாங்கிய பகுதி PQ ன் மீது செயல்படும் விசையின் எண்மதிப்பு FpQ = IaBsin(π/2) = IaB. இது மேல்நோக்கிய திசையில் செயல்படுகிறது என்பதை வலக்கைத் திருகு விதியைப் பயன்படுத்தி அறியலாம்.

பகுதி QR மீது செயல்படும் விசையின் எண்மதிப்பு FQR = IbBsin(π/2−θ) = IbBcosθ. இவ்விசையின் திசை படம்தில் காட்டப்பட்டுள்ளது.

பகுதி RS மீது செயல்படும் விசையின் எண் மதிப்பு FRS = IaBsin(π/2) = IaB. இவ்விசைகீழ்நோக்கிய திசையில் செயல்படுகிறது.

பகுதி SP மீது செயல்படும் விசையின் எண் மதிப்பு Fsp = IbBsin (π/2+ θ) = IbBcos θ. இவ்விசையின் திசை படம்தில் காட்டப்பட்டுள்ளது.

FQR மற்றும் FSP ஆகிய இவ்விரு விசைகள் சமமாகவும் ஒன்றுக்கொன்று எதிர்த்திசையில் அமைந்து ஒரே நேர்க்கோட்டிலும் செயல்படுவதால் அவை ஒன்றையொன்று சமன் செய்துவிடுகின்றன. ஆனால், FPQ மற்றும் FRS ஆகிய இவ்விரு விசைகள் சமமாகவும் ஒன்றுக்கொன்று எதிர்த்திசையில் இருந்தாலும் ஒரே நேர்க்கோட்டில் செயல்படாததால், அவை இரட்டையை உருவாக்கி வளையத்தின் மீது ஒரு திருப்புவிசையை செலுத்துகின்றன.

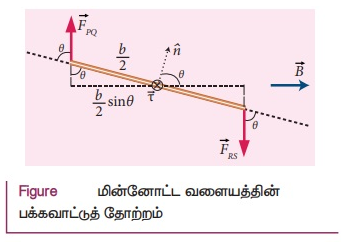
அச்சு ABஐப் பொறுத்து பகுதி PQன் மீது செயல்படும் திருப்புவிசையின் எண்மதிப்பு

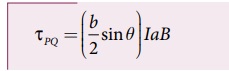
இது AB திசையில் செயல்படுகின்றது. அச்சு ABஐப் பொறுத்து பகுதி RSன் மீதுசெயல்படும் திருப்புவிசையின் எண்மதிப்பு

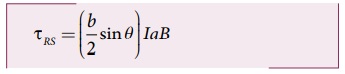
மேலும் இதுவும் ABன் திசையிலேயே செயல்படுகின்றது (படம்).

அச்சு ABஐப் பொறுத்து வளையத்தின் மீது செயல்படும் மொத்த திருப்புவிசை

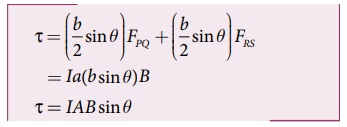
இது ABன் திசையில் செயல்படுகிறது. வெக்டர் வடிவில்,

மேலேயுள்ள சமன்பாட்டினை காந்த இருமுனை திருப்புத்திறனின் அடிப்படையில் எழுதினால்,

இத்திருப்புவிசை வளையத்தை சுழலச் செய்து அதன் ஓரலகு செங்குத்து வெக்டரை காந்தப்புலத்தின் திசையில் ஒருங்கமைக்கும் விதத்தில் செயல்படுகின்றது.

செவ்வக வளையத்தில் சுற்றுகள் இருப்பின், திருப்புவிசை,

சிறப்பு நேர்வுகள் :

(அ) θ = 90° அல்லது வளையத்தின் தளம் காந்தப்புலத்திற்கு இணையாக உள்ள போது, மின்னோட்ட வளையத்தின் மீதான திருப்புவிசை பெருமம் ஆகும்.

(ஆ) θ = 0°/180° அல்லது வளையத்தின் தளம் காந்தப்புலத்திற்கு செங்குத்தாக உள்ள போது, மின்னோட்ட வளையத்தின் மீதான திருப்புவிசை சுழியாகும்.

11. கால்வனோமீட்டர் ஒன்றை அம்மீட்டர் மற்றும் வோல்ட்மீட்டராக எவ்வாறு மாற்றுவது என்பதை விவரிக்கவும். 

கால்வனோ மீட்டரை அம்மீட்டராக மாற்றுதல்: 

• அம்மீட்டர் மின்சுற்றில் பாயும் மின்னோட்டத்திற்கு மிகக் குறைந்த மின்னோட்டத்தை தடுக்காது. 

• ஒரு கால்வனோ மீட்டரை அம்மீட்டராக மாற்ற, குறைந்த மின்தடை ஒன்றை பக்க இணைப்பில் இணைக்க வேண்டும். 

• குறைந்த மின்தடை − இணைதடை மின்தடை 

• I−மின்சுற்றில் பாயும் மின்னோட்டம் 

• Ig−கால்வனோ மீட்டர் வழியே பாயும் மின்னோட்டம்

• Rg−கால்வனோ மிட்டர் வழியே பாயும் மின்தடை 

• இணைதடை மின் தடை வழியே பாயும் மின்னோட்டம் 

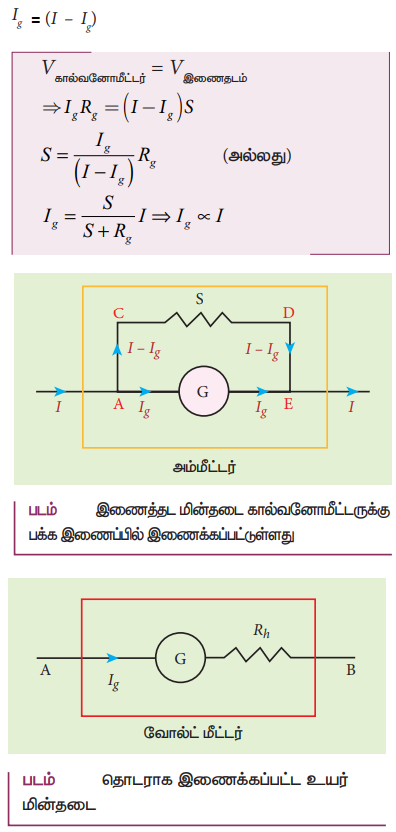
• கால்வனோ மீட்டரில் ஏற்படும் விலக்கம் அதன் வழியே பாயும் மின்னோட்டத்திற்கு நேர்த்தகவில் இருக்கும்.

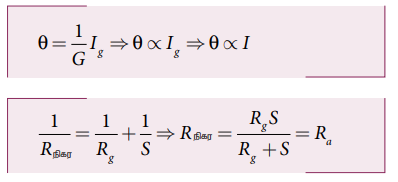
• Ra என்பது மிகக் குறைவு.

• ஒரு நல்லியல்பு அம்மீட்டடரின் மின்தடை சுழியாகும்.

கால்வனோமீட்டரை வோல்ட் மீட்டராக மாற்றுதல். 

• வோல்ட் மீட்டர் உயர்ந்த மின்தடையைப் பெற்றிருக்கும். 

• ஒரு கால்வனோ மீட்டரை வோல்ட் மீட்டராக மாற்ற, தொடரிணைப்பாக உயர் மின்தடை ஒன்றை இணைக்க வேண்டும். 

• Rg−கால்வனோ மீட்டர் மின்தடை

• Ig−கால்வனோ மீட்டர் மின்னோட்டம் 

• Rh−உயர்ந்த மின்தடை தொடராக இணைக்கப்பட்டுள்ளதால், 

• ஒரு நல்லியல்பு வோல்ட் மீட்டர் முடிவிலா மின்தடையைப் பெற்றிருக்கும். 

12. ஆம்பியரின் சுற்று விதியின் உதவியுடன் நீண்ட வரிச்சுருளின் உட்புறம் மற்றும் வெளிப்புறத்தில் ஏற்படும் காந்தப்புலத்தைக் கணக்கிடுக. 

• L நீளமும் N சுற்றுகளும் கொண்ட நீண்ட வரிச்சுருள் ஒன்றைக் கருதுக. 

• வரிச்சுருளின் நீளத்துடன் ஒப்பிடும் போது அதன் விட்டம் மிகவும் சிறியது. 

வரிச்சுருளின் உள்ளே காந்தப்புலத்தைக் கணக்கிடுதல். 

• செவ்வக வடிவ ஒரு சுற்று abcd ஐக் கருதுக. ஆம்பியரின் சுற்று விதியிலிருந்து 

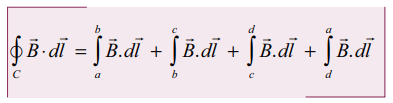
bc மற்றும் da பக்கங்களின் நீளக்கூறுகள் வரிச்சுருளின் அச்சின் வழியே அமைந்துள்ளது. 

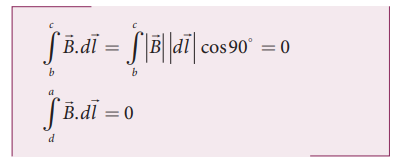
வரிச்சுருளுக்கு வெளியேயும் காந்தப்புலம் சுழி 

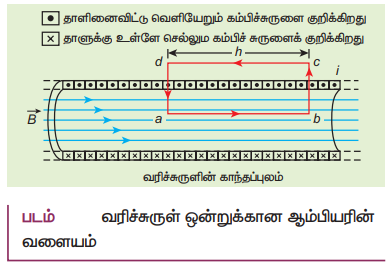
L−வரிச்சுருளின் நீளம் 

I−வரிச்சுருளில் பாயும் மின்னோட்டம் 

N−ஓரலகு நீளத்திற்கான சுற்றுகளின் எண்ணிக்கை

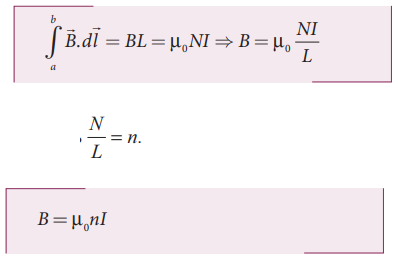
13. மின்னோட்டம் பாயும் இரு இணைக் கடத்திகளுக்கு இடையே உருவாகும் விசைக்கான கோவையைத் தருவி. 

• நீண்ட இணையான மின்னோட்டம் பாயும் இரண்டு கடத்திகள் r இடைவெளியில் காற்றில் பிரித்து வைக்கப்பட்டுள்ளன. 

• I1 மற்றும் பாயும் I2 − A மற்றும் B கடத்தி வழியே செல்லும் மின்னோட்டங்கள் 

• A கடத்தியில் I1 மின்னோட்டத்தினல் r தொலைவில் ஏற்படும் நிகர காந்தப்புலம்

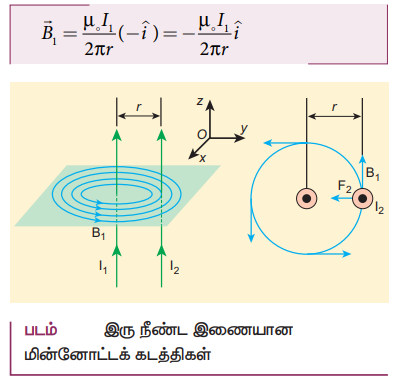
• காந்தப்புலத்தின் திசை தாளின் தளத்திற்கு செங்குத்தாக உள்நோக்கிச் செல்கிறது. 

• B கடத்தியின் dl நீளமுள்ள சிறு கூறின் மீது செயல்படும் லாரன்ஸ் விசை 

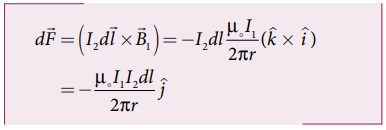
• A கடத்தியினால், B கடத்தியின் ஓரலகு நீளத்தில் செயல்படும் விசை

• I2 மின்னோட்டம் பாயும் B கடத்தியினால் r தொலைவிலுள்ள A கடத்தியின் dl நீளமுள்ள சிறு கூற்றினால் ஏற்படும் காந்தப்புலம்,

• காந்தப்புலத்தின் திசை தாளின் தளத்திற்கு செங்குத்தாகவும் வெளிநோக்கியும் செயல்படுகிறது. 

• கடத்தி A யில் உள்ள dl நீள சிறு கூறின் மீது செயல்படும் காந்தவிசை

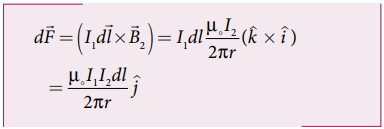
• A கடத்தியின் ஓரலகு நீளத்தில் செயல்படும் விசை

• ஈர்ப்பு விசை − ஒரே திசையில் மின்னோட்டம் பாயும் 

• விலக்கு விசை − எதிரெதிர் திசைகளில் மின்னோட்டம் பாயும்

14. காந்தவியல் லாரன்சு விசையைப் பற்றி குறிப்பு வரைக. 

• q மின்னூட்டம் கொண்ட மின்துகளானது என்ற காந்தப்புலத்தில், திசைவேகத்தில் இயங்கும் போது உணரும் விசை, லாரன்ஸ் காந்த விசை ஆகும். 

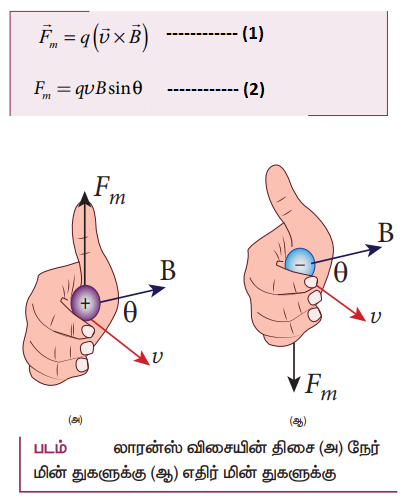
• சமன்பாடு (1) மற்றும் (2)லிருந்து நாம் அறிந்து கொள்வது. 

• அனது காந்தப்புலம் க்கு நேர்த்தகவு. 

• ஆனது திசைவேகம் க்கு நேர்த்தகவு.

• ஆனது திசைவேகம் மற்றும் காந்தப்புலத்திற்கு இடைப்பட்ட கோணத்தின் நேர்த்தகவு. 

• ஆனது மின்னூட்டத்தின் எண்மதிப்பிற்கு நேர்த்தகவு 

• இன் திசை, மற்றும் இன் திசைகளுக்கு எப்போதும் செங்குத்தாகவே இருக்கும். 

• எதிர்மினதுகள் உணரும் இன் திசையானது, நேர்மின்துகள் உணரும் இன் திசைக்கு எதிர் திசையில் இருக்கும். 

• மின்துகள் qவின் திசைவேகம் யானது காந்தப்புலம் இன் திசையில் இருந்தால் சுழியாகும்.

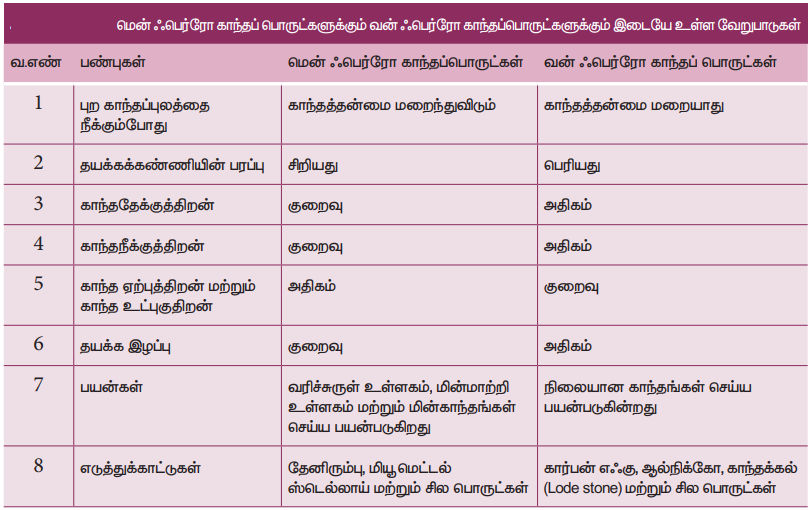
15. மென் மற்றும் வன் பெர்ரோ காந்தப் பொருள்களின் பண்புகளை ஒப்பிடுக.

16. காந்தப்புலத்தில் வைக்கப்பட்டுள்ள மின்னோட்டம் பாயும் கடத்தியின் மீது செயல்படும் விசைக்கான கோவையை வருவி.

• மின்னோட்டம் பாயும் கடத்தி ஒன்றை காந்தப் புலத்தில் வைக்கும் போது, கடத்தி உணரும் விசை மின்துகளின் மீது செயல்படும். லாரன்ஸ் விசையின் கூடுதலுக்குச் சமம். 

• I மின்னோட்டம் பாயும் A குறுக்கு வெட்டுப் பரப்பு கொண்ட dl நீளமுள்ள கம்பியின் சிறுபகுதி ஒன்றை கருதுக. 

• கட்டுறா எலக்ட்ரான்கள் மின்னோட்டத்தின் திசைக்கு எதிராக நகர்கின்றன. 

• மின்னோட்டம் மற்றும் இழுப்பு திசைவேகம் Vd க்கும் உள்ள தொடர்பு 

• I = neAvd 

• காந்தப்புலத்தினுள், உணரும் சராசரி விசை,

n − ஓரலகு பருமக்கான கட்டுறா எலக்ட்ரான்களின் எண்ணிக்கை

n = N/V

V = Adl 

• லாரன்ஸ் விசை=

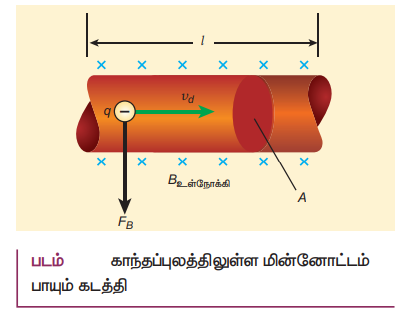
i) காந்தப்புலத்தின் திசைக்கு இணையாக மின்னோட்டம் பாயும் போது

θ = 0°

F = 0 

ii) காந்தப்புலத்தின் திசைக்கு செங்குத்தாக மின்னோட்டம் பாயும் போது,

θ = 90° 

F = BIl

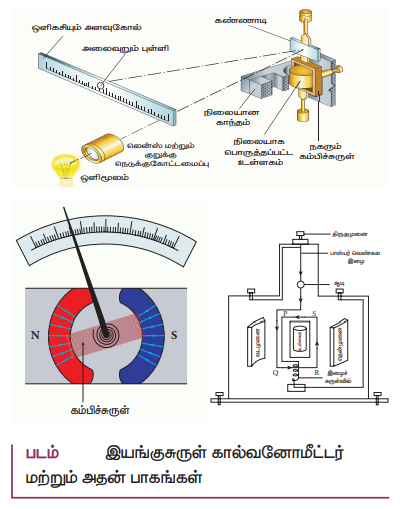
17. இயங்கு சுருள் கால்வனோ மீட்டர் ஒன்றின் தத்துவம் மற்றும் இயங்கும் முறையை விளக்கவும்.

ஒரு மின்சுற்றின் வழியே பாயும் மின்னோட்டத்தைக் கண்டறியலாம். 

தத்துவம் 

மின்னோட்டம் பாயும் வளையம் ஒன்றை சீரான காந்தப்புலத்தில் வைக்கும் போது அது ஒரு திருப்புவிசையை உணரும். 

வேலை செய்யும் முறை: 

• செவ்வக கம்பிச்சுருள் −PQRS 

• PQ=RS=l (நீளம்)

• OR=SP= b(அகலம்) 

• I→PQRS வழியே பாயும் மின்னோட்டம், குரைலாட வடிவ காந்தத்தில் அரைக்கோள காந்த முனைகள் ஓர் ஆரவகை காந்தப்புலத்தை தோற்றுவிக்கும். 

• QR மற்றும் SP பக்கங்கள் எப்பொழுதும் காந்தப்புலத்திற்கு B இணையாக இருக்கும் மற்றும் எவ்வித விசையையும் உணராது. 

• PQ மற்றும் RS பக்கங்கள் எப்பொழுதும் காந்தப் புலத்திற்கு B செங்குத்தாக இருப்பதால் விசையை உணரும்.

• N சுற்றுகள் கொண்டால்,

 τ=NABI          ………………1

• மீட்சி இரட்டையின் எண் மதிப்பு, முறுக்குக் கோணம் θ விற்கு நேர்த்தகவில் இருக்கும். 

 τ=Kθ               ………………2

• K=மீட்சி இரட்டை அல்லது சுருள் வில்லின் முறுக்கமாறிலி 

• சமன்பாடு 1 மற்றும் 2ஐ ஒப்பிட்டால், 

NABI = Kθ

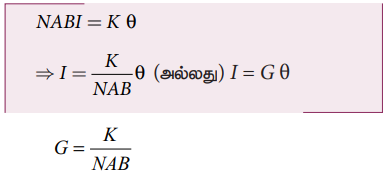
G−கால்வனோ மீட்டர் மாறிலி அல்லது கால்வனோ மீட்டரின் மின்னோட்ட சுருக்கக் கூற்றெண்.