குவாண்டம் எண்கள்

குவாண்டம் எண்கள்

அணுவில் உள்ள ஒரு எலக்ட்ரானை நான்கு குவாண்டம் எண்கள் அடங்கிய தொகுப்பின் மூலம் வரையறுக்க இயலும். அவையாவன முதன்மைக் குவாண்டம் எண் (n), கோண உந்த குவாண்டம் எண் (l), காந்த குவாண்டம் எண் (m) மற்றும் தற்சுழற்சி குவாண்டம் எண் (s) அலைச்சார்பு Ψ-க்கு ஷ்ரோடிங்கர் அலைச் சமன்பாட்டிற்கு தீர்வு காணும் போது பெறப்படும் தீர்வானது முதல் மூன்று குவாண்டம் எண்களைக் (n,l மற்றும் m) கொண்டிருக்கும். நான்காவது குவாண்டம் எண்ணானது எலக்ட்ரானின் தற்சுழற்சியின் காரணமாக அமைகிறது. எனினும், ஒரு பொருள் தனக்குத் தானே சுழல்வது என்பது மரபு இயக்கவியல் கொள்கைப்படி சரியானது அல்ல.

முதன்மைக் குவாண்டம் எண் (n) 

அணுக்கருவினைச் சுற்றி எலக்ட்ரான்கள் சுழன்று வரும் ஆற்றல் மட்டத்தினை இக்குவாண்டம் எண் குறிப்பிடப்படுகிறது. இது 'n' என்ற எழுத்தால் குறிப்பிடப்படுகிறது.

1) முதன்மைக் குவாண்டம்எண் (n) ன் மதிப்புகள் 1, 2, 3. . . .

n = 1 என்பது K கூட்டினையும் (Shell) n = 2 என்பது L கூட்டினையும் n = 3, 4, 5 என்பன முறையே M, N, O ஆகிய கூடுகளையும் குறிப்பிடுகின்றன.

2) ஒரு குறிப்பிட்ட கூட்டில் இடம் பெறும் அதிகபட்ச எலக்ட்ரான்களின் எண்ணிக்கையினை 2n2 என்ற வாய்பாட்டின் மூலம் பெறலாம்.

3) 'n' ஆனது எலக்ட்ரானின் ஆற்றல் மதிப்பினைத் தருகிறது.

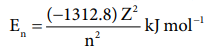
மேலும் அணுக்கருவிலிருந்து எலக்ட்ரான் அமைந்துள்ள தூரமானது 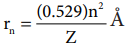 என்ற சமன்பாட்டால் தரப்படுகிறது.

கோண உந்தக் குவாண்டம் எண் (l)

1) இது 'l' என்ற எழுத்தால் குறிப்பிடப்படுகிறது. இது பூஜ்யம் முதல் (n-1) வரையிலான மதிப்புகளைப் பெறுகிறது. இங்கு n என்பது முதன்மைக் குவாண்டம் எண்னைக் குறிப்பிடுகிறது.

2) ஒவ்வொரு l மதிப்பும் ஒரு துணைக்கூட்டினைக் (sub - shell or orbital) குறிப்பிடுகிறது l = 0, 1, 2, 3 மற்றும் 4 ஆகியன முறையே s, p, d, f மற்றும் g ஆர்பிட்டால்களைக் குறிப்பிடுகின்றன.

3) ஒரு துணைக் கூட்டில் (ஆர்பிட்டாலில்) இடம் பெறும் அதிகபட்ச எலக்ட்ரான்களின் எண்ணிக்கையினை 2(2l + 1) என்ற வாய்பாட்டினைப் பயன்படுத்திக் கணக்கிடலாம்.

4) ஆர்பிட்டால் கோண உந்தத்தினை கணக்கிட இக்குவாண்டம் எண் பயன்படுகிறது.

ஆர்பிட்டால் கோண உந்தம் =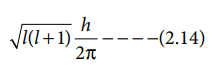

காந்தக் குவாண்டம் எண் (ml)

1) இது ‘ml’ என்ற குறியீட்டால் குறிக்கப்படுகிறது. இக்குவாண்டம் எண்  -l முதல் பூஜ்ஜியத்தினை உள்ளடக்கி +l வரையிலான முழுக்களின் மதிப்பினைப் பெறுகிறது. l = 1 எனில் m = -1, 0, +1

2) ஒருகுறிப்பிட்ட 'l' மதிப்பிற்கு உரிய 'm'-ன் வெவ்வேறு மதிப்புகளானது, முப்பரிமாண வெளியில் ஆர்பிட்டால்களின் திசையமைப்பினைக் குறிப்பிடுகிறது.

3) காந்தப்புலத்தில் நிறமாலை வரிகள் பிரியும் நிகழ்வான சீமன்விளைவு. இக்குவாண்டம் எண்ணிற்கான ஆய்வு அடிப்படையிலான ஒரு நிரூபனமாகும்.

4) குவாண்டம் எண் ‘l’ ஆனது கோண உந்தத்தின் எண் மதிப்பினைத் தரும் நிலையில், காந்தக் குவாண்டம்எண் (ml) அதன் திசையினைத் தருகிறது.

தற்சுழற்சிக் குவாண்டம் எண் (ms)

1) இக்குவாண்டம் எண் எலக்ட்ரான்களின் தற்சுழற்சியினைக் குறிப்பிடுகிறது. இது 'ms' என்ற குறியீட்டால் குறிப்பிடப்படுகிறது.

2) எலக்ட்ரானானது அணுவின் அணுக்கருவினை சுற்றிவருவதோடு இல்லாமல் தனக்குத்தானே சுழன்று வருகிறது. இதனை, எலக்ட்ரானது தனது சுய அச்சில் தனக்குத்தானே கடிகாரமுள் சுழலும் திசையிலேயோ அல்லது அதற்கு எதிர் திசையிலேயோ சுழல்கிறது எனக் குறிப்பிடுவது வழக்கம். இதனை காட்சிப் படுத்தல் உண்மையல்ல எனினும் தற்சுழற்சியினை, காந்தப் புலத்தில் உணரப்படும் ஒரு பண்பினைக் குறிப்பிடுவதாக நம்மால் புரிந்து கொள்ளமுடியும்.

3) கடிகார முள் சுழலும் திசை அல்லது கடிகார முள் சுழலுவதற்கு எதிர்திசையில் எலக்ட்ரான்களின் தற் சுழற்சியினைப் பொறுத்து அதிகபட்சமாக இரு மதிப்புகளை இக்குவாண்டம் பெற வாய்ப்புள்ளது

4) ms ன் மதிப்புகள் +1/2 மற்றும் -1/2 ஆகும்.

அட்டவணை 2.1 குவாண்டம் எண்கள் மற்றும் அவற்றின் முக்கியத்துவம்

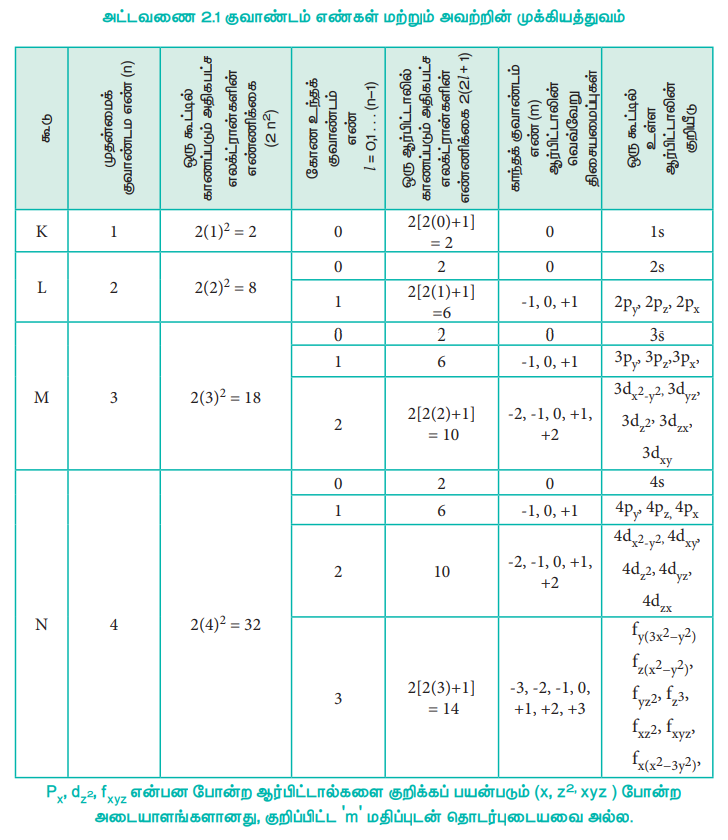
Px, dz2, fxyz என்பன போன்ற ஆர்பிட்டால்களை குறிக்கப் பயன்படும் (x, z2, xyz) போன்ற அடையாளங்களானது, குறிப்பிட்ட 'm' மதிப்புடன் தொடர்புடையவை அல்ல.

தன் மதிப்பீடு

3) 4 வது ஆற்றல் மட்டத்தில் (n=4) எத்தனை ஆர்பிட்டால்கள் இருப்பதற்கு வாய்ப்பு உள்ளது?

தீர்வு

4வது ஆற்றல் மட்டத்தில் உள்ள ஆர்பிட்டால்களின் எண்ணிக்கை = n2 எனவே நான்காவது ஆற்றல் மட்டத்தில் உள்ள ஆர்பிட்டால்களின் எண்ணிக்கை = (4)2 = 16.

1. ஆர்பிட்டால்களின் வடிவங்கள்

ஷ்ரோடிங்கர் அலைச் சமன்பாட்டின் தீர்வுகள் ஐகன் மதிப்புகள் என்றழைக்கப்படும். அனுமதிக்கப்பட்ட ஆற்றல் மதிப்புகளைத் தருகின்றன. ஐகன் மதிப்போடு தொடர்புடைய ஐகன் சார்புகள் அணு ஆர்பிட்டால்கள் என அழைக்கப்படுகின்றன. ஹைட்ரஜனை ஒத்த ஒரு எலக்ட்ரான் அமைப்பிற்கான ஷ்ரோடிங்கர் அலைச் சமன்பட்டின் தீர்வை (Ψ) கோளக துருவ ஆய அச்சில் (r, θ, ϕ) (spherical polar co-ordinates) பின்வருமாறு குறிப்பிடலாம். 

Ψ (r, θ, ϕ) = R (r). f (θ). g (ϕ) ---------- (2.15) 

இங்கு R(r) என்பது ஆர அலைச் சார்பு (Radial wave function) என அழைக்கப்படுகிறது. மற்ற இருசார்புகளும் கோண அலைச் சார்புகள் (angular wave function) என அழைக்கப்படுகின்றன.

Ψ க்கு என இயற் முக்கியத்துவம் ஏதும் இல்லை எனவும், அலைச் சார்பின் இருமடி |Ψ|2 ஆனது புறவெளியில் (space) கொடுக்கப்பட்ட கனஅளவிற்குள் எலக்ட்ரானை காண்பதற்கான நிகழ்தகவோடு தொடர்புடையது எனவும் நாம் அறிவோம். 

அணுக்கருவிலிருந்து உள்ள, தொலைவினைப் பொருத்து |Ψ|2 மதிப்பானது எவ்வாறு மாறுபடுகிறது - (நிகழ்தகவின் ஆரபங்கீடு - Radial distribution of the probability) என்பதனையும் அணுக்கருவிலிருந்து திசையினைப் பொருத்து (நிகழ்தகவின் கோணப்பங்கீடு - angular distribution of the probability |Ψ|2 எவ்வாறு மாறுபடுகிறது என்பதனையும் நாம் ஆய்ந்தறிவோம். 

ஆரப் பங்கீட்டுச் சார்பு

அடிஆற்றல் நிலையில் (ground state) உள்ள ஹைட்ரஜன் அணுவின் ஒற்றை எலக்ட்ரானைக் கருதுக. இந்த எலக்ட்ரானுக்கான குவாண்டம் எண்கள் n = 1 மற்றும் l = 0 அதாவது இந்த எலக்ட்ரான் 1s ஆர்பிட்டாலில் உள்ளது. 1s ஆர்பிட்டாலுக்கான, R (r2) Vs r வரைபடம் படம் (23)ல் கொடுக்கப்பட்டுள்ளது.

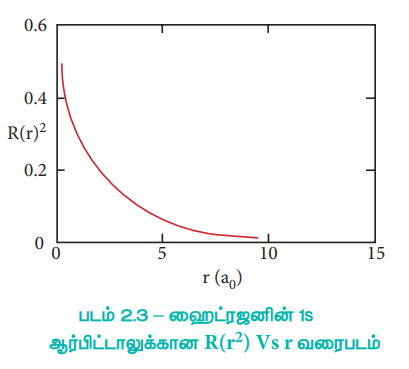
படம் 2.3 – ஹைட்ரஜனின் 1s ஆர்பிட்டாலுக்கான R (r2) Vs r வரைபடம்

மேற்கண்டுள்ள வரைபடத்திலிருந்து, எலக்ட்ரானுக்கும் அணுக்கருவிற்கும் இடையேயான தூரம் குறையும்போது, எலக்ட்ரானைக் காண்பதற்கான நிகழ்த்தகவும் அதிகரிக்கின்றது என அறிய முடிகிறது, r = 0, எனும் போது R (r2) - ன் மதிப்பானது பெருமமாகிறது. அதாவது |Ψ|2 - ன் அதிக பட்ச மதிப்பானது அணுக்கருவினுள் அமைகிறது. எனினும் அணுக்கருவினைச் சுற்றி கொடுக்கப்பட்ட கோளகக் கூட்டில் எலக்ட்ரானைக் காண்பதற்கான நிகழ்தகவே முக்கியமானதாகும். r மற்றும் r + dr ஆகிய ஆரங்களுடைய இரு ஒரு மைய கோளங்களுக்கு இடைப்பட்ட கன அளவு (dV) - யைக் கருதுவோம்.

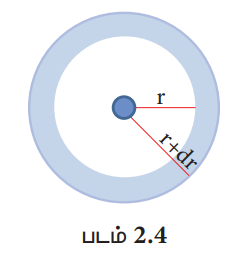
கோளத்தின் கன அளவு V = 4 / 3 (πr3)

dV / dr = 4 / 3 [π (3r2)]

dV = 4 πr2 dr

Ψ2dV = 4 πr2 Ψ2 dr ----------- (2.16)

r மதிப்பிற்கு எதிரான 4πr2 . R(r)2 – ன் வரைபடம் கீழே கொடுக்கப்பட்டுள்ளது.

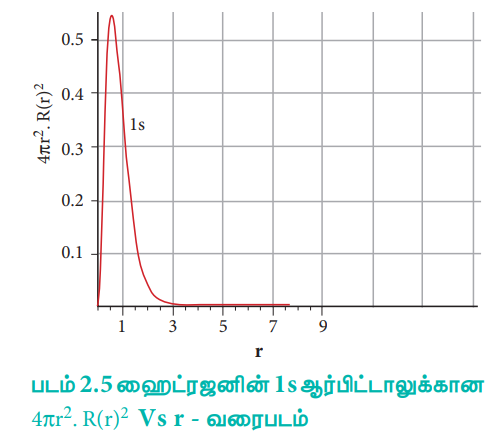
படம் 2.5 ஹைட்ரஜனின் 1s ஆர்பிட்டாலுக்கான 4πr2 . R(r)2 Vs r - வரைபடம்

மேற்கண்டுள்ள வரைபடத்தின் மூலம் அணுக்கருவிலிருந்து 0.52 Å தொலைவில் அதிகபட்ச நிகழ்த்தகவு அமைந்துள்ளது என அறிய முடிகிறது. இத்தொலைவு போர் ஆரத்திற்குச் சமம். இத்தொலைவில் அணுக்கருவினை சுற்றி, எலக்ட்ரானைக் காண்பதற்கான அதிகபட்ச நிகழ்தகவு உள்ளதை இது  குறிப்பிட்டாலும், இத்தொலைவினை தவிர்த்த பிற தொலைவுகளிலும் எலக்ட்ரானை காண்பதற்கான வாய்ப்பு (நிகழ்தகவு) உண்டு. ஹைட்ரஜன் அணுவில் 2s, 3s, 3p மற்றும் 3d ஆர்பிட்டால்களுக்கான ஆர பகிர்வு சார்பினை பின்வருமாறு வரைபடத்தில் குறிப்பிடலாம்.

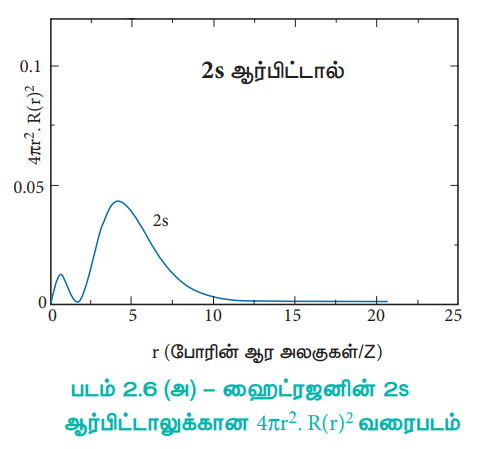
படம் 2.6 (அ) - ஹைட்ரஜனின் 2s ஆர்பிட்டாலுக்கான 4πr2 . R(r)2 வரைபடம்

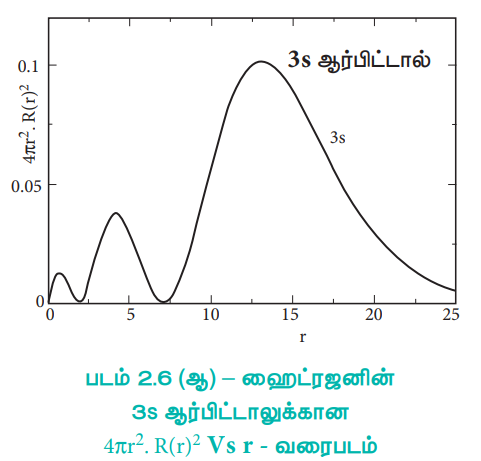
படம் 2.6 (ஆ) - ஹைட்ரஜனின் 3s ஆர்பிட்டாலுக்கான 4πr2 . R(r)2 Vs r - வரைபடம்

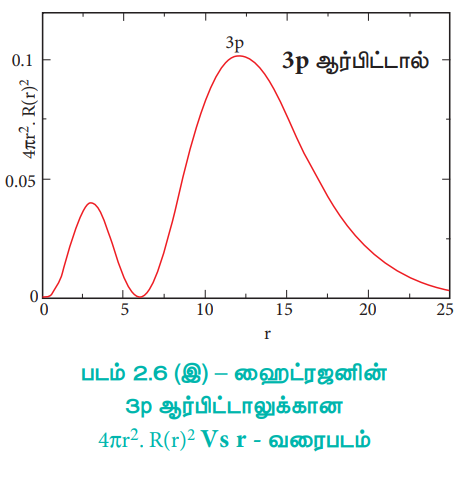
படம் 2.6 (இ) – ஹைட்ரஜனின் 3p ஆர்பிட்டாலுக்கான 4πr2 . R(r)2 Vs r - வரைபடம்

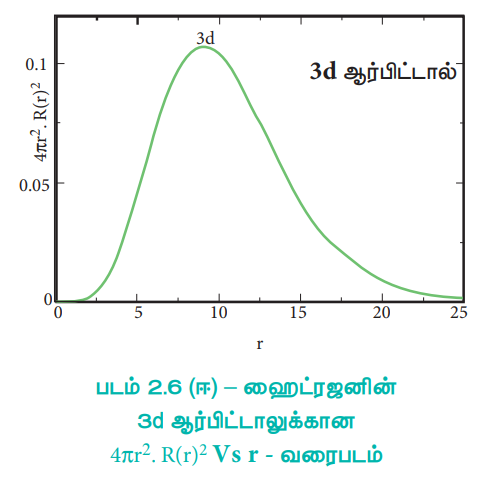
படம் 2.6 (ஈ) – ஹைட்ரஜனின் 3d ஆர்பிட்டாலுக்கான 4πr2 . R(r)2 Vs r - வரைபடம்

2s ஆர்பிட்டாலுக்கு, அணுக்கருவிலிருந்து தொலைவு (r) அதிகரிக்கும்போது, நிகழ்தகவு அடர்த்தி முதலில் அதிகரித்து, ஒரு சிறிய பெரும மதிப்பை அடைகிறது. அதன் பின்னர் பூஜ்ஜியத்திற்கு குறைந்து மீண்டும் மற்றுமொரு பெரும மதிப்பினை அடைந்து பின் பூஜ்ய மதிப்பினையடைகிறது. இவ்வாறு நிகழ்தகவு அடர்த்தி சார்பின் மதிப்பு எப்பகுதியில் பூஜ்யமாகிறதோ அப்பகுதி, கணு புறப்பரப்பு (nodal surface) அல்லது ஆரக்கணு (radial node) என அழைக்கப்படுகிறது. பொதுவாக, ns – ஆர்பிட்டாலானது (n – 1) கணுக்களைப் பெற்றுள்ளன. என கண்டறியப்பட்டுள்ளது. அதாவது 2s ஆர்பிட்டால் ஒரு கணுவையும், 3s ஆர்பிட்டால் இருகணுக்களையும் கொண்டுள்ளது. இது பிற ஆர்பிட்டால்களுக்கும் பொருந்தும். 3p மற்றும் 3d ஆர்பிட்டால்களுக்கான, 4πr2 R(r)2ன் வரைபடமானது, இதனைப் போலவே உள்ளது. ஆனால் இந்நேர்வில் ஆர கணுக்களின் எண்ணிக்கை (n – l - 1) க்குச் சமம். இங்கு 'n' என்பது முதன்மைக் குவாண்டம் எண்ணையும், l என்பது கோண உந்த குவாண்டம் எண்ணையும் குறிப்பிடுகின்றது.

கோணப் பகிர்வு சார்பு (Angular distribution function)

அணுக்கருவை மையத்தில் கொண்டுள்ள ஒரு கோளத்தில் உள்ள, எலக்ட்ரானைக் கண்டறியும் நிகழ்தகவில் ஏற்படும் மாறுபாடு ஆனது கோண உந்தக் குவாண்டம் எண்ணை பொருத்து அமைகிறது. 1s ஆர்பிட்டாலுக்கு l = 0 மற்றும் m = 0. மேலும் f(θ) = 1 / √2 மற்றும் g(ϕ) = 1 / √2π எனவே, கோண பகிர்வு சார்பு f(θ). g(ϕ) ஆனது 1/2 √π - க்குச் சமம். இது கோணம் θ மற்றும் ϕ -ஐச் சார்ந்து அமைவதில்லை. எனவே, எலக்ட்ரானைக் காண்பதற்கான நிகழ்தகவு அணுக்கருவிலிருந்து உள்ள திசையினைப் பொருத்து அமைவதில்லை. எனவே S ஆர்பிட்டாலின் வடிவம் படம் 2.7ல் கொடுக்கப்பட்டுள்ளவாறு ஒரு சீர்மைக் கோளமாகும்.

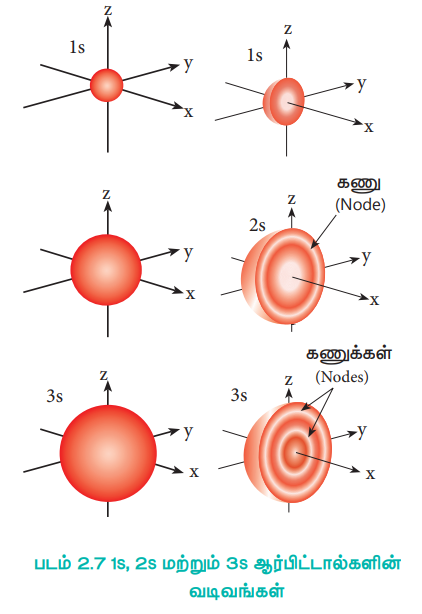
படம் 2.7 1s, 2s மற்றும் 3s ஆர்பிட்டால்களின் வடிவங்கள்

p - ஆர்பிட்டாலுக்கு l = 1, மற்றும் இதற்கு இணையான m மதிப்புகள் முறையே -1, 0 மற்றும் +1 ஆகும். இதற்கான கோண பகிர்வு சார்புகள் சிக்கலானவை, மேலும் இங்கு விவரிக்கப்படவில்லை. 'p’ ஆர்பிட்டாலின்டம்பல் வடிவம் படம் (2.8)ல் கொடுக்கப்பட்டுள்ளது. 'm'ன் மூன்று மதிப்புகளிலிருந்து மூன்று திசையமைப்புடைய ‘p' ஆர்பிட்டால்கள் உள்ளன என அறியமுடிகிறது. இந்த ஆர்பிட்டால்கள் px, py, மற்றும் pz குறியிடப்படுகின்றன. ஆர்பிட்டால்களின் கோணப்பகிர்வின் மூலம் px, py, மற்றும் pz, ஆர்பிட்டால்களின் மடல்கள் (Iobes) முறையே x, y மற்றும் z அச்சுகளின் வழியே அமைந்துள்ளது என அறியலாம்.

படம் 2.8ல் காட்டப்பட்டுள்ளவாறு 2P ஆர்பிட்டால் ஒரு கணுத்தளத்தினை (nodal plane) பெற்றுள்ளது. d ஆர்பிட்டாலுக்கு l = 2, இதற்கு இணையான m மதிப்புகள் முறையே -2, -1, 0, +1, +2. d ஆர்பிட்டாலானது குளோவர் இலையின் வடிவமைப்பினை ஒத்துள்ளது. m-ன் இந்த ஐந்து மதிப்புகளானது, dx2 – y2, dxy, dz2, dyz, dzx ஆகிய ஐந்து ஆர்பிட்டால்கள் உள்ளதைக் காட்டுகிறது. படம் (2.9)ல் காணப்பட்டுள்ளவாறு, 3d ஆர்பிட்டால் இரு கணுத்தளங்களை(nodal planes)பெற்றுள்ளன.

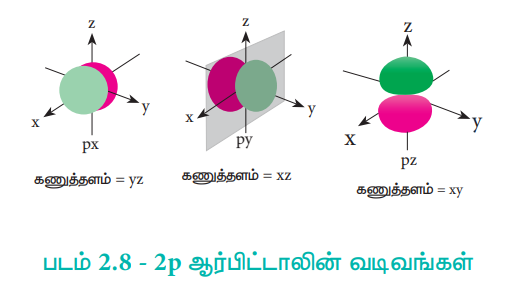
படம் 2.8 - 2p ஆர்பிட்டாலின் வடிவங்கள்

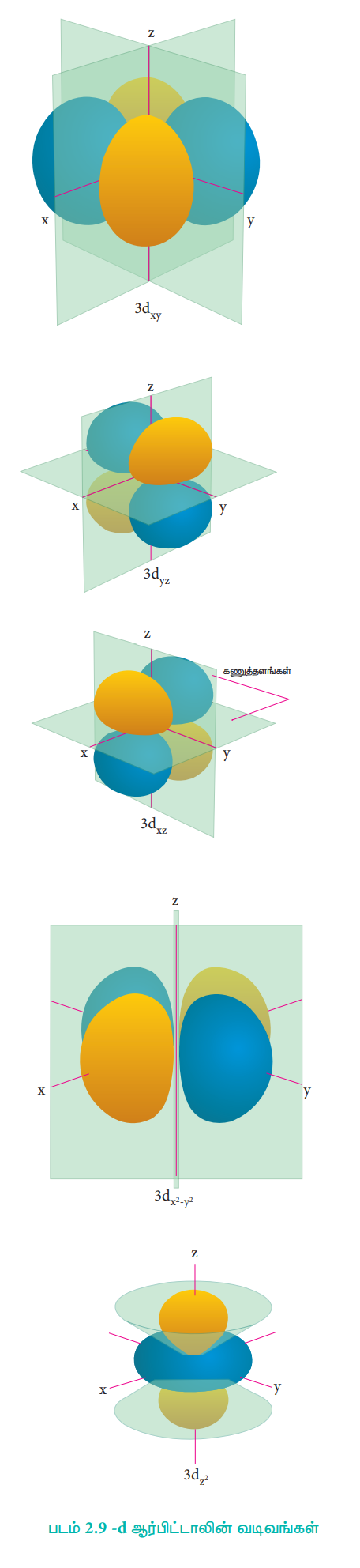
f ஆர்பிட்டாலுக்கு, l = 3 மற்றும் m மதிப்புகள் முறையே -3, -2, -1, 0, +1, +2, +3 ஆகும். இந்த m மதிப்புகளுக்கு இணையாக ஏழு f ஆர்பிட்டால்கள் fy(3x2-y2), fz(x2- y2), fyz2, fz3, fxz2, fxyz, fx(x2- 3y2) காணப்படுகின்றன. 

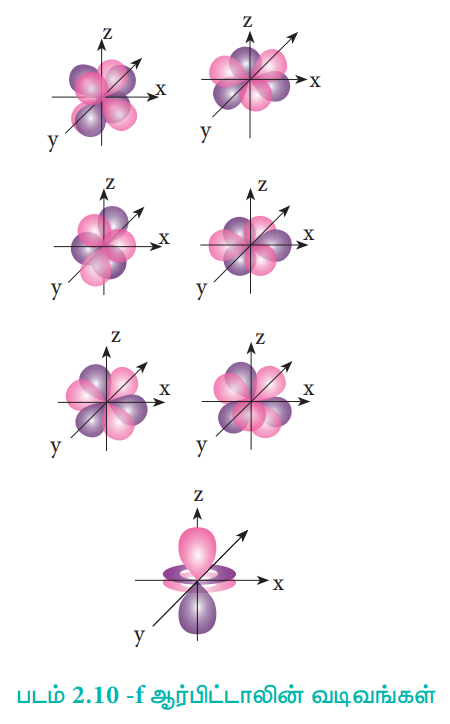
படம் 2.10 - f ஆர்பிட்டாலின் வடிவங்கள்

தன் மதிப்பீடு

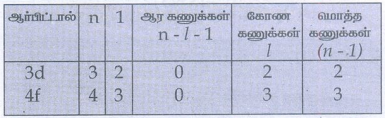
4) 3d மற்றும் 4f ஆர்பிட்டால்களில் காணப்படும் ஆர மற்றும் கோண கணுக்களின் எண்ணிக்கையினைக் கணக்கிடுக.

2. ஆர்பிட்டால்களின் ஆற்றல்கள்

ஹைட்ரஜன் அணுவில் ஒரே ஒரு எலக்ட்ரான் மட்டுமே உள்ளது. இத்தகைய ஒரு எலக்ட்ரானை மட்டுமே பெற்றுள்ள அமைப்பிற்கு, nஆவது வட்டப்பாதையின் உள்ள எலக்ட்ரானின் ஆற்றல் பின்வருமாறு தரப்படுகிறது.

En = [ (-1312.8) Z2] / n2 kJ mol-1

இச்சமன்பாட்டிலிருந்து ஆற்றலானது முதன்மைக் குவாண்டம் எண்ணை மட்டுமே பொருத்து அமைகிறது என நாம் அறிகிறோம். nன் மதிப்பு அதிகரிக்கும் போது, ஆர்பிட்டாலின் ஆற்றலின் மதிப்பும் அதிகரிக்கும். பல்வேறு ஆர்ப்பிட்டால்களுக்கான ஆற்றலின் வரிசை பின்வருமாறு அமைகிறது.

1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f < 5s = 5p = 5d = 5f < 6s = 6p = 6d = 6f < 7s

ஹைட்ரஜன் அணுவில் உள்ள ஒருஎலக்ட்ரான் குறைந்தபட்ச ஆற்றலைப் பெற்றுள்ள 1s ஆர்பிட்டாலில் உள்ளது. இந்நிலை இயல்பு ஆற்றல் நிலை (graund state) என அழைக்கப்படுகிறது. இந்த எலக்ட்ரான் சிறிதளவு ஆற்றலை பெறும் போது 2s, 2p போன்ற அதிக ஆற்றலுடைய ஆர்பிட்டால்களுக்குச் செல்லும். இந்த உயர் ஆற்றல் நிலைகள் கிளர்வுற்றநிலைகள் (excited state) என அழைக்கப்படுகின்றன. எனினும் ஹைட்ரஜனைத் தவிர்த்த பிற அணுக்களுக்கு (பல எலக்ட்ரானை கொண்ட அமைப்புகளுக்கு) மேற்கண்டுள்ள ஆற்றல் வரிசை உண்மையல்ல. அத்தகைய அமைப்புகளுக்கு ஷ்ரோடிங்கர் அலைச் சமன்பாடு சிக்கலானதாகும். இத்தகைய அமைப்பில் உள்ள பல்வேறு ஆர்பிட்டால்களின் ஒப்பீட்டு அளவிலான ஆற்றல் வரிசையினை (n+l) விதி தருகிறது. இவ்விதிப்படி, ஆர்பிட்டாலின் (n+l) மதிப்பு குறைவாக இருப்பின் அதன் ஆற்றலும் குறைவாக இருக்கும். இரு ஆர்பிட்டால்களின் (n+l) மதிப்பு சமமாக இருப்பின், அவ்விரு ஆர்பிட்டால்களில் எந்த ஆர்பிட்டாலுக்கு n மதிப்பு குறைவாக உள்ளதோ அந்த ஆர்பிட்டால் குறைந்த ஆற்றலைப் பெற்றிருக்கும். இவ்விதியினைப் பயன்படுத்தி பல்வேறு ஆர்பிட்டால்களின் ஆற்றலின் வரிசையினை பின்வருமாறு குறிப்பிடலாம்.

அட்டவனை 2.2 பல்வேறு ஆர்பிட்டால்களின் (n+l) மதிப்புகள்

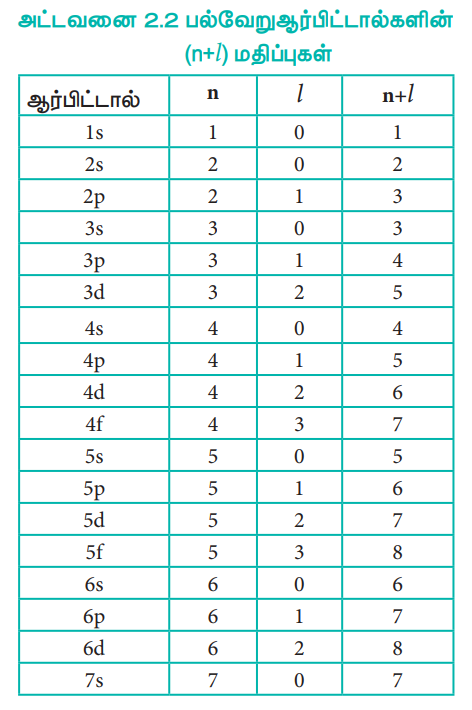
(n+l) விதியின் அடிப்படையில், ஆர்பிட்டால்களின் ஆற்றலின் ஏறுவரிசை பின்வருமாறு

1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < 5d < 6p < 7s < 5f < 6d

ஒரு p ஆர்பிட்டாலுக்கு, மூன்று வகையான திசையமைப்புகள் உள்ளன என்பதனை நாம் அறிவோம். அதாவது Px, Py, மற்றும் Pz ஆகிய இம்மூன்று ஆர்பிட்டால்களின் ஆற்றலும் சமம். இவைகள் சம ஆற்றல் ஆர்பிட்டால்கள் (degenerate orbitals) என அழைக்கப்படுகின்றன. எனினும் மின் மற்றும் காந்தப்புலங்களின் இந்த சமஆற்றல் பண்பு (degeneracy) இழக்கப்படுகிறது.

பல எலக்ட்ரான்களைப் பெற்றுள்ள ஒரு அணுவில், அணுக்கருவிற்கும், எலக்ட்ரான்களுக்கும் இடையேயான நிலை மின்னியல் கவர்ச்சி விசை மட்டுமல்லாமல், எலக்ட்ரான்களுக்கிடையேயான விலக்குவிசையும் காணப்படுகிறது.  இவ்விருவிசைகளும் ஒன்றுக்கொன்று எதிரெதிர் திசைகளில் செயல்படுகின்றன. இதன் விளைவாக அணுக்கருவானது எலக்ட்ரான் மீது செலுத்தும் கவர்ச்சி விசை குறைகிறது. எலக்ட்ரானால் உணரப்படும் நிகர அணுக்கரு மின்சுமையானது செயலுறு அணுக்கரு மின் சுமை (effective nuclear charge) என்றழைக்கப்படுகிறது. இந்த நிகர அணுக்கரு மின்சுமை ஆர்ப்பிட்டால்களின் வடிவமைப்பினைப் பொருத்து அமைகிறது. மேலும் கோண உந்தக் குவாண்டம் எண் ‘l’ ன் மதிப்பு அதிகரிக்கும் போது இதன் மதிப்பு குறைகிறது.

ஒரு குறிப்பிட்ட கூட்டினுள், உள்ள ஆர்பிட்டால்களில் காணப்படும் எலக்ட்ரானால் உணரப்படும் நிகர அணுக்கரு மின்சுமையின் மதிப்பு s > p > d > f என்ற வரிசையில் அமையும். நிகர அணுக்கரு மின்சுமையின் மதிப்பு அதிகமாக இருப்பின், ஆர்பிட்டால்களின் நிலைப்புத் தன்மை அதிகமாக இருக்கும். எனவே, கொடுக்கப்பட்ட ஆற்றல் மட்டத்தில், ஆர்பிட்டால்களின் ஆற்றலின் வரிசை பின்வருமாறு அமையும். s < p < d < f

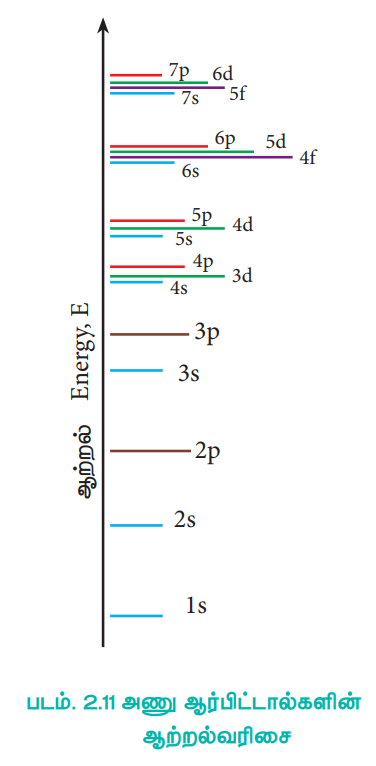
படம். 2.11 அணு ஆர்பிட்டால்களின் ஆற்றல்வரிசை

ஒரே வகையான ஆர்பிட்டால்களின் ஆற்றலானது அணு எண் அதிகரிக்கும் போது குறையும். உதாரணமாக ஹைட்ரஜனின் 2s ஆர்பிட்டாலின் ஆற்றலானது, லித்தியத்தின் 2s ஆர்பிட்டாலின் ஆற்றலை விட அதிகம், இதைப் போலவே லித்தியத்தின் 2s ஆர்பிட்டாலின் ஆற்றல் சோடியத்தின் 2s ஆர்பிட்டாலின் ஆற்றலை விட அதிகம். அதாவது, E2s (H) > E2s (Li) > E2s (Na) > E2s (K).

தன்மதிப்பீடு

5) ஹைட்ரஜன் அணுவில் உள்ள ஒரு எலக்ட்ரானின் அடிநிலை ஆற்றல் - 13.6.ev. இரண்டாவது கிளர்வுற்ற நிலையில் இந்த எலக்ட்ரானின் ஆற்றல் என்ன?

தீர்வு

En =  (−13.6 / n2 )ev V/atom

முதலாவது கிளர்வுற்ற நிலை n = 2 எனவே இரண்டாவது கிளர்வுற்ற நிலை n = 3 ஆகும்.

∴ E3 =  (−13.6 / 32 )ev/atom = −1.51 ev / atom