வட்ட வரிச்சுருள்

வட்ட வரிச்சுருள்

வரிச்சுருளின் இரண்டு முனைகளும் ஒன்றுடன் ஒன்று தொடும் வகையில் வளைக்கப்பட்ட வட்ட அமைப்பே வட்ட வரிச்சுருளாகும். இது ஒரு மூடப்பட்ட வளையம் போன்று காணப்படும். இது படம் 3.q22 இல் காட்டப்பட்டுள்ளது. வட்ட வரிச்சுருளின் உள்ளே காந்தப்புலம் மாறாத எண்மதிப்பைப் பெருற்றிருக்கும். அதே நேரத்தில் வட்ட வரிச்சுருளின் உட்பகுதியில் (P புள்ளியில்) மற்றும் வெளிப்பகுதியில் (Q புள்ளியில்) காந்தப்புலம் சுழியாகும்.

(அ) வட்ட வரிச்சுருளின் திறந்தவெளி உட்புறப்பகுதி

P புள்ளியில் ஏற்படும் காந்தப்புலம் Bp ஐ நாம் கணக்கிட , r1 ஆரமுடைய ஆம்பியரின் சுற்று 1 ஐ புள்ளி P ஐச் சுற்றி படம் 3.43 இல் காட்டியுள்ளவாறு

அமைக்கலாம். கணக்கீட்டை எளிமையாக்க ஆம்பியர் சுற்றை வளையமாகக் கருதுவோம். எனவே, வளையத்தின் சுற்றளவு அதன் நீளமாகும்.

வளையம் 1 க்கான ஆம்பியரின் சுற்றுவிதி

இங்கு வளையம் 1 எவ்விதமான மின்னோட்டத்தையும் சூழ்ந்திருக்கவில்லை நடப்பட்ட = 0

புள்ளி P யில் உள்ள காந்தப்புலம் சுழியானால் மட்டுமே இது சாத்தியமாகும். அதாவது

(ஆ) வட்ட வரிச்சுருளின் வெளிப்புறத்தில் உள்ள திறந்தவெளிப்பகுதி

Q புள்ளியில் உள்ள காந்தப்புலம் BQ வைக் கணக்கிட படம் 3.43 இல் காட்டியுள்ளவாறு Q புள்ளியைச் சுற்றி r3ஆரமுடைய ஆம்பியரின் வளையம் 3 ஐ அமைக்கலாம்.

வளையம் 3 க்கான ஆம்பியரின் சுற்றுவிதி

இங்கு ஒவ்வொரு சுற்றிலும் தாளின் தளத்தை விட்டு வெளியே வரும் மின்னோட்டம், தாளின் தளத்திற்கு உள்ளே செல்லும் மின்னோட்டத்தினால் சமன்செய்யப்படுகிறது. எனவே, Iமூடப்பட்ட = 0

புள்ளி Q வில் உள்ள காந்தப்புலம் சுழியானால் மட்டுமே இது சாத்தியமாகும். அதாவது

(இ) வட்ட வரிச்சுருளின் உள்ளே

S புள்ளியில் உள்ள காந்தப்புலம் Bs ஐக் கணக்கிட, படம் 3.43 இல் உள்ளவாறு S புள்ளியைச் சுற்றி r2ஆரமுடைய ஆம்பியரின் வளையம் 2 ஐ அமைக்கலாம்.

வளையத்தின் நீளம் L2 = 2πr2

வளையம் 2 க்கான ஆம்பியரின் சுற்றுவிதி

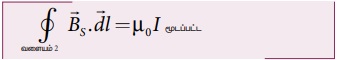
வட்டவரிச்சுருளின் வழியே பாயும் மின்னோட்டத்தை I எனவும் சுற்றுகளின் எண்ணிக்கையை N எனவும் கொண்டால்

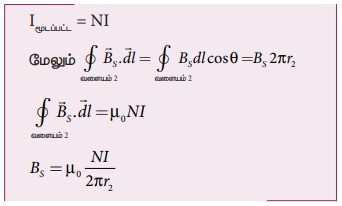
 ஓரலகு நீளத்திற்கு சுற்றுகளின் எண்ணிக்கை n= N/2πr2. எனவே S புள்ளியில் உள்ள காந்தப்புலம்