Я«ЋЯ«БЯ«┐Я«цЯ«хЯ«┐Я«»Я«▓Я»Ї - Я«фЯ«▓ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»Ђ(Linear Approximation and Differential of a function of several variables) | 12th Maths : UNIT 8 : Differentials and Partial Derivatives
12 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї : Я«ЁЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«»Я««Я»Ї 8 : Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐ Я«хЯ«ЋЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї
Я«фЯ«▓ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»Ђ(Linear Approximation and Differential of a function of several variables)
Я«фЯ«▓ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»Ђ(Linear Approximation and Differential of a function of several variables)
Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«єЯ«░Я««Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«ц Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»Ђ Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»ІЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«цЯ»Є Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«ц Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ, Я«ЄЯ«цЯ»ЄЯ«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ«▓ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»ЂЯ«ЪЯ»ѕЯ«» Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ 8.10
A = {(x,y) | a < x < b, c < y < d} РіѓРёЮ2, F : A Рєњ РёЮ , Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (x0,y0) Рѕѕ A Я«јЯ«ЕЯ»ЇЯ«Ћ.
(i) (x0,y0) РѕѕA Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї F-Я«ЕЯ»Ї Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
F(x,y) = F(x0,y0) + РѕѓF/Рѕѓx|(x0,y0) (x-x0) + РѕѓF/Рѕѓy|(x0,y0) (y РђЊ y0) --------(12)
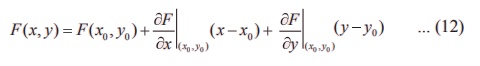
(ii) F-Я«ЕЯ»Ї Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»Ђ
РѕѓF = РѕѓF / Рѕѓx (x, y)dx + РѕѓF / Рѕѓy (x, y)dy, -------------(13)
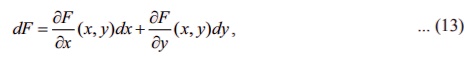
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ dx = Рѕєx , dy = Рѕєy Я«јЯ«Е Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»ЂЯ«ЪЯ»ѕЯ«» Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»Ђ Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«фЯ«▓ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»ЂЯ«ЪЯ»ѕЯ«» Я««Я»єЯ«»Я»ЇЯ««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«џЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«еЯ«ЙЯ««Я»Ї Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я»Ї Я«јЯ«ЕЯ«┐Я«ЕЯ»ЂЯ««Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я«ЅЯ«ЪЯ»ѕЯ«» Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ІЯ«ЪЯ»Ђ Я«еЯ«ЙЯ««Я»Ї Я«еЯ«┐Я«▒Я»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї.
Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ 8.11
A = {(x,y,z) |a < x < b, c < y < d, e < z < f } Ріѓ РёЮ3 , F: A Рєњ РёЮ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (x0, y0, , z0 , ) РѕѕA Я«јЯ«ЕЯ»ЇЯ«Ћ.
(i) (x0, y0, , z0 , ) Рѕѕ A Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї F Я«ЕЯ»Ї Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
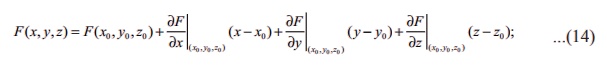
Я«јЯ«Е Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ
(ii) F-Я«ЕЯ»Ї Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»Ђ
dF = РѕѓF / Рѕѓx (x, y, z)dx + РѕѓF / Рѕѓy (x, y, z) dy + РѕѓF / Рѕѓz (x, y, z)dz , ------------ (15)
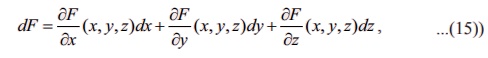
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ dx = Рѕєx, dy = Рѕєy Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї dz = Рѕєz Я«јЯ«Е Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«хЯ«ЪЯ«┐Я«хЯ«ЋЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐, Я«њЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«ц Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»Ђ f -Я«ЕЯ»Ї, x0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ x0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї y = f (x) -Я«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«цЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ. Я«ЄЯ«цЯ»ЂЯ«фЯ»ІЯ«▓Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«ц Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»Ђ F-Я«ЕЯ»Ї (x0,y0) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ (x0,y0) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї z = F(x,y) Я«јЯ«ЕЯ»ЇЯ«▒Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ»Ђ Я«цЯ«│Я«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ.
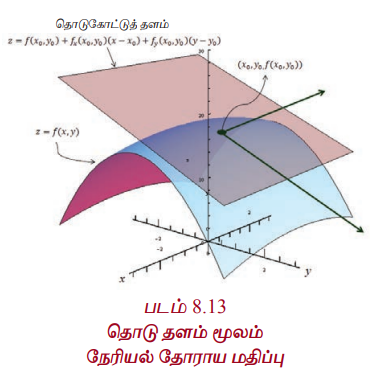
Я«фЯ«ЪЯ««Я»Ї 8.13 Я«цЯ»іЯ«ЪЯ»Ђ Я«цЯ«│Я««Я»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 8.16
w(x,y,z) = x2y + y2z + z2x, x, y, z РѕѕРёЮ , Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»Ђ dw Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я««Я»ЂЯ«цЯ«▓Я«┐Я«▓Я»Ї wx, wy, Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Wz Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
wx = 2xy + z2,wy = 2yz + x2 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї wz = 2zx + y2.
Я«јЯ«ЕЯ«хЯ»Є (15)-Я«ЕЯ»Ї Я«фЯ«ЪЯ«┐ Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»Ђ
dw = (2xy + z2)dx + (2yz +x2)dy + (2zx+y2)dz
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 8.17
U(x, y, z) = x2 - xy + 3sin z, x, y, z РѕѕРёЮ Я«јЯ«ЕЯ«┐Я«▓Я»Ї (2,-1,0) Я«ЄЯ«▓Я»Ї U Я«ЄЯ«ЕЯ»Ї Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
(14)-Я«ЕЯ»Ї Я«фЯ«ЪЯ«┐ Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
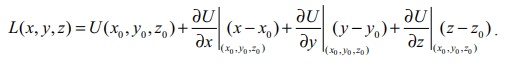
Ux = 2x - y,Uy = -x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Uz = 3cos z .
(x0, y0, z0 ) = (2,-1,0), Я«јЯ«ЕЯ«хЯ»Є Ux (2,-1,0) = 5, Uy (2,-1,0) = -2 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Uz (2,-1,0) = 3.
Я«єЯ«ЋЯ«хЯ»Є, L(x, y, z) = 6+5(x-2) - 2(y+1) + 3(z - 0) = 5x -2y + 3z - 6 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ (2,-1, 0) Я«ЄЯ«▓Я»Ї U -Я«ЕЯ»Ї Я«еЯ»ЄЯ«░Я«┐Я«»Я«▓Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.