சார்பினது சார்பு விதி (Function of Function Rule)

சார்பினது சார்பு விதி (Function of Function Rule)

இரு மாறிகள் x, y இல் அமைந்த சார்பு F என்க. சில நேரங்களில் இந்த மாறிகள் அதே மதிப்பகத்தைக் கொண்ட வேறு ஒரு மாறியின் சார்பாகவும் இருக்கலாம், எனவே சார்பு F ஒரே ஒருமாறியைத்தான் சார்ந்துள்ளது. எனவே சார்பு F -ஐ நாம் ஒரு மாறி சார்பாகக் கருதி dF/dt -ஐ பற்றிப்படிக்கலாம். இது தற்செயலானது அல்ல, இதை நிரூபிக்க முடியும்.

தேற்றம் 8.2

W(x, y) என்பது ∂W / ∂x , ∂W / ∂y என்ற பகுதி வகைக்கெழுக்கள் உள்ள x, y என்ற இரு மாறிகளில் அமைந்த சார்பு என்க. x, y என்ற இருமாறிகளும் t என்ற ஒரு மாறியைப் பொருத்து வகையிடக்கூடிய சார்புகள் எனில் t-ஐப் பொருத்து W -ம் வகையிடக்கூடிய சார்பாகும்.

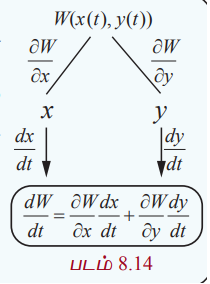
படம் 8.14

மேற்கண்ட தேற்றத்தை விளக்க ஓர் எடுத்துக்காட்டைக் காண்போம்.

எடுத்துக்காட்டு 8.18

F(x,y) = x2 - 2y2 + 2xy மற்றும் x(t) = cos t, y(t) = sint, t ∈ [0, 2π) என்ற சார்பிற்கு மேற்கண்ட தேற்றத்தைச் சரிபார்க்கவும்.

தீர்வு

F(x,y) = x2 - 2y2 + 2xy மற்றும் x(t) = cost, y(t) = sint என்க.

F(x,y) = cos2 t - 2sin2 t + 2 cost sint என்பதால் F என்பது t என்ற ஒரு மாறியில் அமைந்த சார்பாகும். சங்கிலி விதியைப் பயன்படுத்த

dF / dt = 2cost(-sin t) - 4sin t cos t + 2(-sin2t + cos2 t)

= -6cos t sin t +2(- sin2 t + cos2 t).

மறுபுறம்

∂F / ∂x dx / dt + ∂F / ∂y dy/ dt = (2x + 2y) dx / dt + (2x – 4y) dy/dt

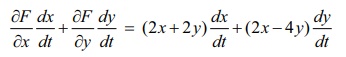
= 2(cos t + sin t)(-sin t ) +2(cos t – 2sin t)(cos t)

= -6cos t sin t + 2(- sin2 t + cos2 t).

= dF/dt 

எடுத்துக்காட்டு 8.19

g(x,y) = x2 - yx + sin(x + y), x(t) = e3t, y(t) = t2, t ∈ℝ எனில் dg / dt- ஐக் காண்க.

தீர்வு

கிளை வரைபடத்தைப் பயன்படுத்தி dg / dt -ஐக் காண்போம்.

இதற்கு முதலில் ∂g/∂x , ∂g/∂y , dx/dt மற்றும் dy/dt  -ஐக் காண்போம்.

∂g/∂x = 2x – y + cos(x+y), ∂g/∂y = -x + cos(x+y), dx/dt = 3e3t மற்றும் dy/dt = 2t

எனவே dg/dt = ∂g/∂x dx/dt + ∂g/∂y dy/dt

= (2x - y + cos(x+y)) 3e3t + (-x + cos(x+y))(2t) 

= (2e3t  - t2 + cos(e3t +t2))3e3t +(-e3t + cos(e3t + t2))(2t)

= 6e6t - 3t2e3t + 3e3t cos(e3t + t2) - 2te3t + 2t cos(e3t +t2) 

மேலும் W (x,y) என்ற சார்பு சில நேரங்களில் x = x(s, t), மற்றும் y = y(s,t), s, t ∈ℝ எனவும் இருக்கலாம். அப்போது W என்ற சார்பு S மற்றும் t இவற்றைச் சார்ந்துள்ளதாக கருதலாம். x, y என்ற இரு மாறிகளுக்கும் S, t -ஐப் பொருத்து பகுதி வகைக்கெழுவும், W -க்கு x,y ஐப் பொருத்து பகுதி வகைக்கெழுவும் உள்ளது எனில் பின்வரும் தேற்றத்தைப் பயன்படுத்தி W -க்கு S மற்றும் t-ஐப் பொருத்து பகுதி வகைக்கெழுவைக் கணக்கிட முடியும்.

தேற்றம் 8.3

W(x,y) என்பது x, y என்ற இரு மாறிகளில் அமைந்த ∂Ꮃ/∂x ,∂Ꮃ/∂y என்ற பகுதி வகைக்கெழுக்கள் கொண்ட சார்பு என்க. x = x(s,t) மற்றும் y = y(s,t), s, t ∈ℝ என்ற இரு மாறிகளுக்கும் S மற்றும் t-ஐப் பொருத்த பகுதி வகைக்கெழுக்கள் உண்டு எனில், 

∂W/ ∂s = ∂W/∂x ∂x/∂s + ∂W/∂y ∂y/∂s, ------(17)

∂W/ ∂t = ∂W/∂x ∂x/∂t + ∂W/∂y ∂y/∂t, ------(18)

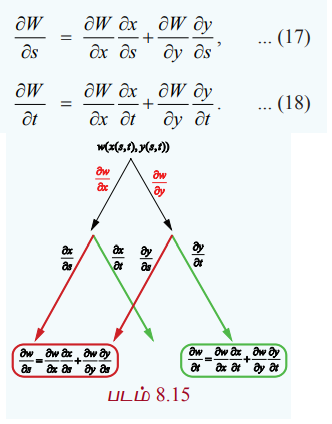
படம் 8.15

இப்பாடப்பகுதியில் மேற்கண்ட தேற்றத்திற்கு நிரூபணம் தேவையில்லை எனக் கருதி விடப்படுகின்றது. மேற்கண்ட தேற்றம் மிகவும் பயனுள்ளது. எடுத்துக்காட்டாக x = r cosθ , மற்றும் y = sinθ,r ≥ 0, θ ∈ ℝ என்ற சூழலைக் கருத்தில் கொள்வோம். (கார்டிசியன் வடிவத்திலிருந்து துருவ வடிவத்திற்கு மாற்ற) மேற்கண்ட தேற்றத்தை n மாறிகள் கொண்ட சார்புகளுக்கும் பொதுமைப்படுத்தலாம்.

சில எடுத்துக்காட்டுகளைக் காண்போம்.

எடுத்துக்காட்டு 8.20

சார்பு g(x,y) = 2y + x2, x = 2r - s, y = r2 + 2s,r,s ∈ℝ எனில்∂g/∂r , ∂g/∂s ஆகியவற்றைக் காண்க.

தீர்வு

கிளை வரைபடத்தைப் பயன்படுத்தி ∂g/∂r , ∂g/∂s -ஐக் காண்போம்.

∂g/∂x = 2x , ∂g/∂y = 2 ∂x/∂r  = 2, ∂x/∂s = -1, ∂y/∂r =  2r , மற்றும் ∂y/∂s = 2

தற்போது

∂g/∂r = ∂g/∂x  ∂x/∂r  + ∂g/∂y ∂y/∂r =2x(2) + 2(2r) = 12r – 4s.

மேலும்,

∂g/∂s = ∂g/∂x  ∂x/∂s  +  ∂g/∂y  ∂y/∂s = 2x(-1) + (2)2 = 2s – 4r + 4.