கணிதவியல் - நேரியல் தோராய மதிப்பு (Linear Approximation) | 12th Maths : UNIT 8 : Differentials and Partial Derivatives
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 8 : வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள்
நேரியல் தோராய மதிப்பு (Linear Approximation)
நேரியல் தோராய மதிப்பு மற்றும் வகையீடுகள்(Linear Approximation and Differentials)
நேரியல் தோராய மதிப்பு (Linear Approximation)
இப்பிரிவில், ஒரு புள்ளியில் ஒரு சார்பின் தோராய மதிப்பினை அறிமுகப்படுத்துவோம். நேரியல் தோராய மதிப்பினைப் பயன்படுத்தி கொடுக்கப்பட்ட புள்ளியின் அருகில் சார்பினை மதிப்பிடுவோம். பின்பு ஒரு மாறியுடைய மெய்ச்சார்பின் வகையீட்டை அறிமுகப்படுத்துவோம். இதுவும் பயன்பாட்டுக்கு உதவியாக இருக்கும்.
f: (a, b) → ℝ என்பதை வகையிடத்தக்கச் சார்பாகவும் மற்றும் x∈ (a, b) எனவும் கொள்க. x என்ற புள்ளியில் f வகையிடத்தக்கது. எனவே
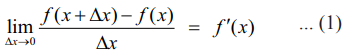
∆x சிறிய மதிப்பு எனில் (1)-ன் மூலம்
f (x + ∆x) - f (x) ≈ f’(x) ∆x; -------------- (2)
அதாவது, f (x+ ∆x) ≈ f (x) + f'(x)∆x, -------------- (3)
இங்கு ≈ என்பது “தோராய மதிப்பிற்குச்” சமம். மேலும் சாராமாறி x இலிருந்து x + ∆x க்கு மாறும்போது f (x) சார்பு f (x + ∆x) க்கு மாறுவதைக் கவனிக்கவும். எனவே ∆x சிறிய மாற்றமாகவும் ∆f அல்லது ∆y வெளியீடாகவும் இருக்கும்போது சமன்பாடு (2)ஐ பின்வருமாறு மாற்றி எழுதலாம்.
வெளியீட்டில் ஏற்படும் மாற்றம் = ∆y = ∆f = f (x+ ∆x) - f (x) ≈ f'(x) ∆x.
f (x) மற்றும் f'(x)∆x ஐ பயன்படுத்தி f (x+ ∆x)-ன் தோராய மதிப்பைக் கணக்கிட சமன்பாடு (3) பயன்படுவதைக் காணலாம். மேலும் ஒரு குறிப்பிட்ட x0 க்கு y(x) = f (x0)+ f’ (x0)(x-x0), x ∈ℝ, என்பது (x0, f(x0)) என்ற புள்ளியில் f -க்கான தொடுகோட்டின் சமன்பாட்டைத் தருகின்றது. இது x0 க்கு அருகில் f -ன் சிறந்த தோராய மதிப்பைத் தருகின்றது. இது பின்வரும் வரையறைக்கு வழி வகுக்கின்றது.
வரையறை 8.1 (நேரியல் தோராய மதிப்பு)
f : (a,b) → ℝ என்பதை வகையிடத்தக்கச் சார்பாகவும், x0∈ (a,b) எனவும் கொள்க. x0 என்ற புள்ளியில் f -ன் தோராய மதிப்பு L-ன் வரையறை
L(x) = f (x0) + f'(x0)(x-x0), ∀x∈ (a,b) ஆகும். ... (4)
சமன்பாடு (3)-லிருந்து
f(x+∆x) ≈ f(x) + f’(x) ∆x,
என்பதை நாம் காணலாம்.
இது f (x+ ∆x)-ன் தோராய மதிப்புகாண பயனுள்ளதாகும்.
இங்கு x-ன் மதிப்பு x0 -ஐ நெருங்கும்போது f (x) -க்கான ஒரு சிறந்த தோராய மதிப்பை x0 என்ற புள்ளியில் f -ன் நேரியல் தோராய மதிப்பு, தருகின்றது.
ஏனெனில் , x -ன் மதிப்பு x0–ஐநெருங்கும்போது x0 இல் f தொடர்ச்சியானது
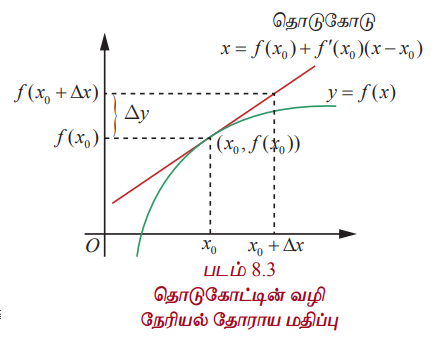
படம் 8.3 தொடுகோட்டின் வழி நேரியல் தோராய மதிப்பு
பிழை = f (x) - L(x) = f (x) - f (x0)- f'(x0)(x - x0) ------ (5)
பூச்சியத்தை நெருங்குகின்றது. மேலும் f (x) = mx+c, எனில் ஏதேனும் ஒரு x ∈ (a,b)-க்கு அதன் நேரியல் தோராய மதிப்பு L(x) = (mx0 + c)+m(x - x0) = mx + c = f (x) ஆகும். இந்த நிலையில் தோராய மதிப்பானது அந்த சார்பாகவே உள்ளது. (இது வியப்பூட்டுவதாக இல்லையா?)
எடுத்துக்காட்டு 8.1
f (x) = √1+x, x ≥ - 1 என்ற சார்பிற்கு நேரியல் தோராய மதிப்பை x0 = 3 இல் காண்க. இதைப் பயன்படுத்தி f (3.2)-ஐ மதிப்பிடுக.
தீர்வு
சமன்பாடு (4)-இலிருந்து L(x) = f (x0) + f '(x0)(x-x0) என நாம் அறிவோம். x0 = 3, ∆x = 0.2 மற்றும் f (3) = √1+3 = 2 மேலும்
f'(x) = 1/2√1+x எனவே f’(3) = 1/2√1 + 3 = 1/4
L(x) = 2+ 1/4 (x-3) = x/4 + 5/4 என்பது தேவையான நேரியல் தோராய மதிப்பைத் தருகின்றது.
இப்பொழுது f (3.2) = √4.2 ≈ L(3.2) = 3.2/4 + 5/4 = 2.050
உண்மையில் கணிப்பானைப் (calculator) பயன்படுத்தினால்√4.2 = 2.04939