பகுதி வகைக்கெழுக்கள் (Partial Derivatives)

பகுதி வகைக்கெழுக்கள் (Partial Derivatives)

இந்தப் பிரிவில் ஒரு மாறியில் அமைந்த சார்பின் வகைக்கெழுக் கருத்துருவை பல மாறிகளில் அமைந்த மெய் சார்புகளுக்கு எவ்வாறு விரிவுபடுத்துவது என்பது பற்றி காண்போம். முதலில் இரு மாறிகளைக் கொண்ட சார்புகளை எடுத்துக் கொள்வோம். A = {(x,y)| a < x < b, c < y < d}⊂ℝ2 மற்றும் F : A → ℝ என்பது ஒரு மெய்ச்சார்பு என்க. (x0,y0) ∈ A என்க; (x0,y0) என்ற புள்ளியில் x என்ற மாறியில் மட்டும் ஏற்படும் மாற்றத்திற்கேற்ப F இல் ஏற்படும் மாற்றத்தைக் காண்போம். மேற்கூறியவாறு F(x,y0) என்பது x-ஐ மட்டும் சார்ந்துள்ள சார்பு ஆகும். மேலும் இது y = y0 என்ற தளமும் z = F(x,y0) என்ற வளைபரப்பும் வெட்டும் ஒரு வளைவரையாகும். எனவே z = F(x,y0) என்ற வளைவரையின் தொடுகோட்டுச் சாய்வை x = x0 இல் F(x, y0 ) -ன் x-ஐப் பொருத்த வகைக்கெழுவை x = x0 -ல் காண்பதன் மூலம் காணலாம். இதேபோல் z = F(x0,y) என்ற வளைவரையின் சாய்வை F(x0,y)-ன் y-ஐப் பொருத்த வகைக்கெழுவை y = y0 இல் அறிவது மூலம் காணலாம். இந்த முக்கியக் கருத்துக்கள்தான் பின்வரும் பகுதி வகைக்கெழுவின் வரையறைக்கு நம்மை ஊக்குவிப்பதாக அமையும்.

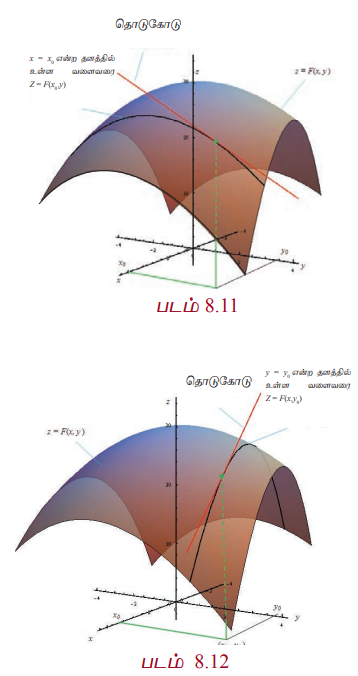
வரையறை 8.8

A = {(x,y)| a < x < b, c < y < d} ⊂ ℝ2, F : A → ℝ மற்றும் (x0,y0) ∈ A என்க.

(i) 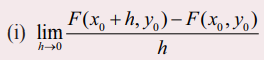ன் மதிப்பு காணத்தக்கது எனில் (x0 , y0) ∈ A இல் F –க்குx -ஐப் பொருத்த பகுதி வகைக்கெழு உள்ளது எனலாம். இந்த எல்லை மதிப்பு ∂F/∂x (x0 , y0) எனக் குறிக்கப்படும்.  ... (10) 

(ii) 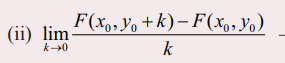ன் எல்லை மதிப்பு காணத்தக்கது எனில் (x0 , y0) ∈ A இல் -  F-க்கு y-ஐ பொருத்த பகுதிவகைக்கெழு உள்ளது எனலாம். இந்த எல்லை மதிப்பு ∂F/∂y (x0 , y0) எனக்குறிக்கப்படும் .... (11)

குறிப்புரை 

1. மூன்று அல்லது அதற்கு மேற்பட்ட மாறிகளைக் கொண்ட சார்புகளுக்கும் பகுதி வகைக்கெழுவானது இதே முறையில்தான் வரையறுக்கப்படும். 

2. ∂F என்பது “பகுதி F” என்றும் ∂x என்பதை “பகுதி x” என்றும் படிக்க வேண்டும். எனவே ∂F/∂x என்பதை “பகுதி F வகுத்தல் பகுதி x” எனப் படிக்க வேண்டும். 

இதை “தோ F வகுத்தல் தோ x” எனவும் படிக்கலாம்.

3. இதேபோல் ∂F/∂x என்பதை “பகுதி F வகுத்தல் பகுதி y” அல்லது “தோ F வகுத்தல் தோ y” எனப் படிக்கலாம்.

4. சில நேரங்களில்∂F/∂x (x0, y0) என்பது Fy(x0, y0 ) அல்லது ∂F/∂x (x,y)| (x, y0 ) எனக் குறிக்கப்படும்.

இதுபோல் ∂F/∂y|(x, y0 ) என்பது Fy(x0, y0 ) அல்லது ∂F/∂y|(x0, y0 )  எனக் குறிக்கப்படும். 

5. x -ஐப் பொருத்து F -ன் பகுதி வகைக்கெழுவைக் காணும்போது கவனிக்க வேண்டியது, மாறி y-ஐ மாறிலியாகக் கருதி x-ஐப் பொருத்து வகைக்கெழு காண வேண்டும். அதாவது எந்த மாறியைப் பொருத்து பகுதி வகைக்கெழு காண வேண்டுமோ அதைத் தவிர மற்ற அனைத்து மாறிகளும் மாறிலியாகக் கருதப்படும். இதனால்தான் நாம் அவற்றை “பகுதி வகைக்கெழு” என்கிறோம். 

6. A-ன் ஒவ்வொரு புள்ளிக்கும் F-க்கு x-ஐப் பொருத்த பகுதி வகைக்கெழு இருக்குமானால் A -க்கு ∂F/∂y (x,y) உள்ளது என்கிறோம். இங்கு ∂F/∂y (x,y) என்பது மறுபடியும் A மீதான ஒருமெய் மதிப்பு சார்பாகும்.

7. (4) -ன்படி வகைக்கெழுவின் எல்லா விதிகளும் (கூட்டல், பெருக்கல் மற்றும் சங்கிலி விதி) சூத்திரங்களும் பகுதி வகைக்கெழுவிற்கும் பொருந்தும். 

ஒரு மாறியில் அமைந்த சார்பிற்கு ஒரு புள்ளியில் வகைக்கெழு இருக்குமானால் அந்தப் புள்ளியில் சார்பு தொடர்ச்சித் தன்மை பெற்றிருக்கும் என்பதை நினைவு கூர்வோம். x, y என்ற இரு மாறிகளில் அமைந்த சார்பு F-ன் ∂F/∂y (x,y) மற்றும் ∂F/∂y (x,y) -ஐ வரையறை செய்தோம். (x,y) இல் F-க்குபகுதி வகைக்கெழு காணத்தக்கது எனில், (x,y) இல் F தொடர்ச்சித் தன்மை உள்ளதாகுமா? இது எப்போதும் மெய்யாக இருக்க வேண்டியது அவசியமில்லை என்பதை பின்வரும் எடுத்துக்காட்டு விளக்குகின்றது. 

எடுத்துக்காட்டு 8.11

xy ≠ 0 எனில் f (x,y) = 0 மற்றும் xy = 0 எனில் f (x,y) =1 என்க.

(i) மதிப்பிடுக: ∂F/∂y (0,0), ∂F/∂y (0,0).

(ii) (0, 0) இல் f  தொடர்ச்சியற்றது என நிறுவுக. 

தீர்வு

ℝ2 இல் x, y -அச்சுகளின் மீது f -ன் மதிப்பு 1 என்பதையும் மற்ற எல்லா இடங்களிலும் 0 என்பதையும் கவனிக்க.

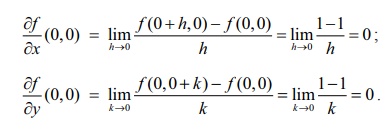
(ii) இதனை நிறுவ y = x என்ற நேர்கோட்டுப் பாதையில் (x,y) → (0,0) எனும்போது f –ன்எல்லைமதிப்பை கணக்கிடுவோம். lim f (x,y) = 0; ஏனெனில் y = x என்ற நேர்கோட்டுப் பாதையில் x ≠ 0 எனில் f (x,y) = 0. ஆனால் f (0, 0) =1 ≠ 0; எனவே (0,0) இல் f  தொடர்ச்சியற்றது.

எடுத்துக்காட்டு 8.12

அனைத்து (x, y) ∈ ℝ2 -க்கும் F(x, y) = x3 y + y2 x+7 எனில்∂F/∂x  (-1,3) மற்றும் ∂F/∂y (-2,1) ஆகியவற்றைக் காண்க.

தீர்வு 

முதலில் ∂F/∂x (x,y) கணக்கிட்டு அதனை (-1,3) இல் மதிப்பிடுவோம். y-ஐ மாறிலியாகக்கொண்டு x -ஐ பொருத்து வகையிடுவோம். 

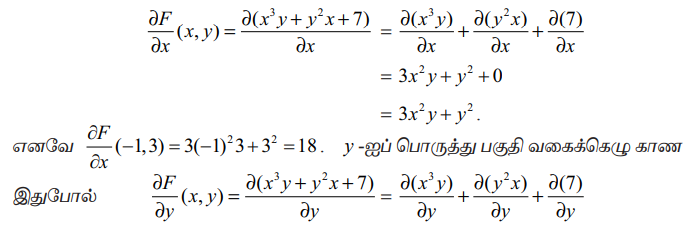
    = x3 + 2yx +0 

    = x3 + 2yx

எனவே ∂F/∂y (-2,1) = (-2)3 + 2(1)(-2) = -12

மேற்கண்ட எடுத்துக்காட்டில் ∂F/∂y (x,y) = 3x2y + y2 என்பது மறுபடியும் இரு மாறிகளைக் கொண்ட சார்பாகும். எனவே இந்தச் சார்பின் x-ஐ பொருத்து அல்லது y-ஐ பொருத்து பகுதி வகைக்கெழு காண முடியும். உதாரணமாக G(x,y) = 3x2y + y2 என எடுத்துக் கொண்டால் ∂G/∂x = 6xy G(x,y) = ∂F/∂y என்பதால் ∂G/∂x = ∂/∂x (∂F/∂x) = 6xy எனக் கிடைக்கிறது. இது ∂2F/∂x2 எனக் குறிக்கப்படும். இது F -இன் x-ஐப் பொருத்த இரண்டாம் வரிசைப் பகுதி வகைக்கெழு என அழைக்கப்படுகிறது.

மேலும் ∂G/∂y = 3x2 + 2y, G(x,y) = ∂F/∂x என்பதால் ∂G/∂y = ∂/∂y (∂F/∂x) = 3x2 + 2y. இதை ∂2F/∂y∂x எனக்குறிக்கலாம். இது x, y -ஐப் பொருத்த F-ன் கலப்புப் பகுதி வகைக்கெழு என அழைக்கப்படுக்கிறது.

இதுபோல் ∂/∂x (∂F/∂y) = 3x2 + 2y எனக் கணக்கிடலாம்.

மேலும் ∂F/∂y (x,y)-ஐ y-ஐப் பொருத்து பகுதி வகைக்கெழு காண ∂2F/∂y2எனக் கிடைக்கிறது. இது F-ன் y-ஐப் பொருத்த இரண்டாம் வரிசை பகுதி வகைக்கெழு காண எனப்படும். எனவே ஏதேனும் ஒரு உட்கணம் {(x,y)| a < x < b, c < y < d}Cℝ2 மீது வரையறுக்கப்பட்ட F என்ற சார்பிற்கு பின்வரும் குறியீடுகள் உள்ளன:

∂2F / ∂x2 = ∂/∂x (∂F/∂x) = Fxx’                     ∂2F / ∂x ∂y =  ∂/ ∂x (∂F/∂y) = Fxy’ 

∂2F / ∂y ∂x =  ∂/ ∂y (∂F/∂x) = Fyx’              ∂2F / ∂y2   =  ∂/ ∂y (∂F/∂y) = Fyy

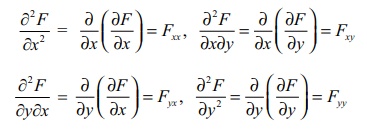
மேற்கண்ட அனைத்தும் F -ன் இரண்டாம் வரிசை பகுதி வகைக்கெழுக்கள் எனப்படும். இவ்வாறு அதிகப்படியான வரிசையுடைய பகுதி வகைக்கெழுக்களையும் வரையறுக்கலாம். 

எடுத்துக்காட்டாக

∂3F / ∂y2∂x =  ∂/ ∂y (∂/ ∂y (∂F/∂x)),  மற்றும்∂3F / ∂x ∂y ∂x =  ∂/ ∂x (∂/ ∂y (∂F/∂x))  

பகுதி வகைக்கெழுக்களுக்கான மேலும் ஒரு எடுத்துக்காட்டைக் காணலாம்.

எடுத்துக்காட்டு 8.13

அனைத்து (x,y) ∈ ℝ2 -க்கும் f (x,y) = sin(xy2) + ex3+5y எனில் ∂F/∂x , ∂F/∂y, ∂2F / ∂y∂x ஆகியவற்றைக் காண்க.

தீர்வு

∂f / ∂x (x,y) -ஐ முதலில் கணக்கிடுவோம். f என்பது இரு சார்புகளின் கூட்டல் எனவே

∂f / ∂x  = ∂ / ∂x sin (xy2) + ∂ / ∂x (ex3+5y)

     = cos(xy2) ∂/∂x (xy2) +ex3+5y ∂ / ∂x(x3+5y)

     = cos(xy2)y2 + ex3+5y 3x2

இதுபோல்,

∂f / ∂y  = ∂ / ∂y sin (xy2) + ∂ / ∂y (ex3+5y)

     = cos(xy2) ∂/∂y (xy2) +ex3+5y ∂ / ∂y(x3+5y)

     = cos(xy2)2xy + 5ex3+5y 

அடுத்து,

∂2f/∂y∂x = ∂/∂y (∂f/∂x) = ∂/∂y (y2cos (xy2) + 3x2 ex3+5y)

            = ∂/∂y (y2cos (xy2)) + ∂/∂y  (3x2 ex3+5y)

               = 2y cos (xy2) + y2(-sin(xy2)2xy) + 3x2 ex3+5y 5

               = 2y cos (xy2) – 2xy3(-sin(xy2)2xy) + 15x2 ex3+5y

இறுதியாக,

∂2f/∂x∂y = ∂/∂x (∂f/∂y) = ∂/∂x (cos (xy2) 2xy + 5 ex3+5y)

= -sin(xy2) y22xy + cos (xy2) 2y + 5 ex3+5y3x2

= 2y cos (xy2) – 2xy3-sin(xy2) + 15x2 ex3+5y

இங்கு முதலில் நாம் கூட்டல் விதியையும் அதையடுத்து சங்கிலி விதியையும் மூன்றாவதாக பெருக்கல் விதியையும் பயன்படுத்தியுள்ளோம் என்பதைக் கவனிக்க. மேலும் fxy = fyz ஆக உள்ளதையும் காணலாம். இது தற்செயலானதா? அல்லது எப்போதும் உண்மையானதா? உண்மையில் சில புள்ளிகளில் சில சார்புகளுக்கு fxy≠ fyz 1, ஆக இருக்கும். பின்வரும் தேற்றம் fxy = fyz ஆக இருப்பதற்கான நிபந்தனையை தரும்.

தேற்றம் 8.1 (கிளெய்ராட்டின் தேற்றம்) 

A = {(x,y)| a < x < b, c < y < d} ⊂ ℝ2, F: A →  ℝ என்ற சார்பு A இல் fxy மற்றும் fyz காணப்பெற்று அவை தொடர்ச்சியானதாகவும் இருக்குமானால் A இல் fxy = fyz என்பதாக இருக்கும்.

இந்நிரூபணம் இப்பாடப்பகுதியில் தவிர்க்கப்படுகின்றது. 

எடுத்துக்காட்டு 8.14 

அனைத்து (x, y) ∈ℝ2 - க்கும் W(x,y) = xy + ey / y2 + 1 எனில் ∂2W/∂y∂x மற்றும் ∂2W/ ∂x∂y காண்க.

தீர்வு 

முதலில் ∂w/∂x (x,y) காண்போம்.

∂w/∂x (x,y) = ∂(x,y)/∂x + ∂( ey / y2 + 1 ) / ∂x

இதிலிருந்து ∂w/∂y (x,y) = y + 0 எனவே ∂2w/∂y∂x (x,y) எனக் கிடைக்கின்றது.

மேலும், ∂w/∂y (x,y) = ∂(x,y)/∂y + ∂( ey / y2 + 1 ) / ∂y

= x+(y2 +1) ey - ey 2y / +(y2 +1)2

எனவே ∂2W / ∂x∂y (x,y) = 1

வரையறை 8.9

A = {(x,y) | a < x < b, c < y < d}⊂ ℝ2 என்க. சார்பு u: A → ℝ2 என்பது  ∂2u / ∂x2 + ∂2u / ∂y2  = 0, ∀(x,y) ∈ A எனுமாறு இருக்குமானால் u: ஆனது A -ல் சீரானது எனலாம். இது இலாபிலாஸின் சமன்பாடு எனப்படும்.

இலாபிலாஸின் சமன்பாடு வெப்பக்கடத்தல், மின்னியல்புலம், திரவ ஓட்டம் ஆகியவற்றில் இயல்பாக நிகழ்கின்றது. 

எடுத்துக்காட்டு 8.15

அனைத்து (x,y) ∈ ℝ2-க்கும் u(x,y) = e-2y cos(2x) எனில் ℝ2 இல் u சீரானது என நிறுவுக. 

தீர்வு

இங்கு u என்ற சார்பு இலாபிலாஸின் சமன்பாட்டை நிறைவு செய்கின்றது எனக் காட்ட வேண்டும். ux (x,y) = e-2y (-2) sin(2x) எனவே uxx (x,y) = e-2y(-2) (2)cos(2x) ஆகும்.

இதேபோல் uy(x,y) = e-2y(-2)cos(2x) எனவே uyy (x,y) = (-2) (-2)e-2y cos(2x) ஆகும்.

uxx + uyy = -4e-2y   cos(2x) + 4e-2y cos(2x) = 0. எனவே ℝ2 இல் u சீரானது.