இரு மாறிகள் உடைய சார்புகளின் எல்லை மற்றும் தொடர்ச்சித் தன்மை(Limit and Continuity of Functions of Two Variables)

இரு மாறிகள் உடைய சார்புகளின் எல்லை மற்றும் தொடர்ச்சித் தன்மை(Limit and Continuity of Functions of Two Variables) 

வரையறை 8.6 (சார்பின் எல்லை)

A = {(x,y)| a < x < b,c < y < d}⊂ ℝ2 F: A → ℝ என்க. F பின்வரும் நிபந்தனைகளை நிறைவு செய்யுமானால் (u,v) இல் F -இன் எல்லை L எனப்படும்:

L-ன் ஒவ்வொரு அண்மைப்பகுதி (L - Ɛ, L + Ɛ), Ɛ > 0-க்கும் 

(x.y) ∈ Bδ ((u,v))\{(u,v)}, δ > 0 ⇒ f (x) ∈ (L- Ɛ, L + Ɛ) எனுமாறு (u,v) -ன் ஒரு δ -அண்மைப்பகுதி Bδ ((u,v)) ⊂ A இருக்கும். 

இதை lim ( x , y ) →(u,v) F ( x, y ) = L என எழுதலாம்.

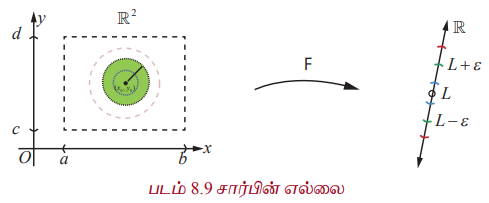
ஒரு மாறியில் அமைந்த சார்புகளை ஒப்பிடும்போது இரு மாறியில் அமைந்த சார்பின் எல்லை காணும் முறை நுட்பமானது ஆகும். இங்கு (u,v) -க்கான ஒவ்வொரு சாத்தியமான பாதை வழியாகவும் (x, y) என்பது (u,v) -ஐ நெருங்கும்போது F(x,y) -ன் மதிப்பு, ஒரே மதிப்பு L-ஐ நெருங்க வேண்டும். (நேர்கோடுகளாக இல்லாத பாதைகளையும் சேர்த்து) எல்லை முறையை படம் 8.9 விளக்குகின்றது.

ஒரு மாறியில் அமைந்த சார்புகளுக்கான எல்லை விதிகள் (எல்லை தேற்றங்கள்) பல மாறிகளைக் கொண்ட சார்புகளுக்கும் பொருந்தும்.

தற்போது ஒரு மாறியில் அமைந்த சார்புகளின் தொடர்ச்சித் தன்மையை பின்பற்றி இரு மாறிகளாலான சார்புகளின் தொடர்ச்சித் தன்மையை வரையறுப்போம்.

வரையறை 8.7 (தொடர்ச்சித் தன்மை)

A= {(x,y)| a < x < b,c < y < d}⊂ℝ2, F : A → ℝ என்ற சார்பு F (u,v) இல் தொடர்ச்சியானது எனில் பின்வருவனவற்றை நிறைவு செய்ய வேண்டும். 

(1) (u,v) இல் F வரையறுக்கப்பட்டுள்ளது

(2) lim( x , y ) →(u,v) F ( x, y ) = L இருக்கிறது 

(3) L = F(u,v).

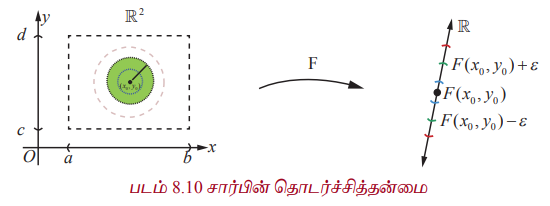
படம் 8.10 சார்பின் தொடர்ச்சித்தன்மை

குறிப்புரை

(1) படம் 8.10 இல் L = F(x0, y0) என்பது (x0, y0) இல் தொடர்ச்சித்தன்மையை விளக்கும். 

(2) f (x1, x2,..., xn)-ன் தொடர்ச்சித் தன்மையும் மேற்கூறிய முறையிலேயே வரையறுக்கப்படும். இரு மாறிகளுடைய சார்புகளின் தொடர்ச்சித் தன்மை பற்றிய சில எடுத்துக்காட்டுகளைக் காண்போம். 

எடுத்துக்காட்டு 8.8

அனைத்து (x,y) ∈ ℝ2 -க்கும் f (x,y) = (3x – 5y + 8) / (x2 + y2  + 1) 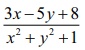  எனில் ℝ2 இல் f தொடர்ச்சியானது எனக்காட்டுக. 

தீர்வு

(a,b) ∈ ℝ2 என்பது ஏதேனும் ஒரு புள்ளி என்க. (a, b) இல் f -ன் தொடர்ச்சித் தன்மை பற்றி ஆராய்வோம்.

அதாவது (a,b) இல் f -ன் தொடர்ச்சித் தன்மைக்கான மூன்று நிபந்தனைகளையும் சரிபார்க்கலாம்.

மேலும் (a, b), என்பது ℝ2 இல் உள்ள ஏதேனும் ஒரு புள்ளி என்பதால் f என்ற சார்பு ℝ2-ன் எல்லா புள்ளிகளிலும் தொடர்ச்சித் தன்மையுடையது என முடிவு செய்யலாம். 

எடுத்துக்காட்டு 8.9  

f(x,y) = , (xy) / (x2 + y2), (x,y) ≠ (0,0) மற்றும் f (0,0) = 0 என்ற சார்பை எடுத்துக் கொள்வோம். இந்தச் சார்பு f , (0,0)-ஐத் தவிர ℝ2 -ன் மற்ற எல்லா புள்ளிகளிலும் தொடர்ச்சித்தன்மையுடையது என நிறுவுக. 

தீர்வு

ஒவ்வொரு (x,y) ∈ ℝ2 -க்கும் f வரையறுக்கப்பட்டுள்ளதைக் கவனிக்கவும். முதலில் (a,b) ≠ (0,0) இல் f-ன் தொடர்ச்சித் தன்மையை சரிபார்ப்போம். எடுத்துக்காட்டாக (a,b) = (2,5) எனில் f(2,5)= 10/29 மேற்கண்ட எடுத்துக்காட்டு போலவே 

 (2,5) இல் f  தொடர்ச்சித் தன்மையுடையது என்பது தெளிவாகிறது. 

இதுபோன்ற வாதங்களைக் கொண்டு (a,b) ≠ (0,0) ஆக உள்ள ஒவ்வொரு புள்ளியிலும் f தொடர்ச்சித் தன்மையுடையது எனலாம். தற்போது (0,0) இல் தொடர்ச்சியைக் காண்போம். வரையறையின்படி f (0,0) = 0. அடுத்தது நாம் 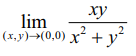எல்லை மதிப்பு உள்ளதா அல்லது இல்லையா எனப் பார்க்க வேண்டும். 

முதலில் (0,0) வழிச் செல்லும் y = mx நேர்க்கோட்டுப்பாதையில் எல்லை மதிப்பை சரிபார்க்கலாம்.

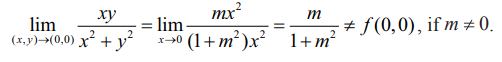
எனவே m -ன்வெவ்வேறான மதிப்புகளுக்கு வெவ்வேறான m / 1 + m2 -ன் மதிப்புகள் கிடைக்கின்றன.

எனவே 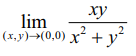-ன் மதிப்பு இல்லை. அதனால் (0,0) இல் f தொடர்ச்சியானது அல்ல.

எனவே (0, 0)-ஐத் தவிர மற்ற எல்லா புள்ளிகளிலும் f தொடர்ச்சியானது ஆகும். 

எடுத்துக்காட்டு 8.10

g(x,y) = 2x2 y / x2 + y2 , (x,y) ≠ (0,0) மற்றும் g(0,0) = 0 எனில் ℝ2 இல் g தொடர்ச்சியானது எனநிறுவுக. 

தீர்வு

சார்பு g எல்லா (x, y) ∈ℝ2க்கும் வரையறுக்கப்பட்டது என்க. மேற்கண்ட எடுத்துக்காட்டுகளைப் போல் (x, y) ≠ (0, 0) ஆக உள்ள எல்லா புள்ளிகளுக்கும், g தொடர்ச்சியானது என எளிதாக சரிபார்க்கலாம். அடுத்து (0,0) இல் g -ன் தொடர்ச்சித் தன்மையை சரிபார்க்கலாம். (0,0) இல் g-க்கு எல்லை உள்ளது மற்றும் L = g(0, 0) = 0 எனில்

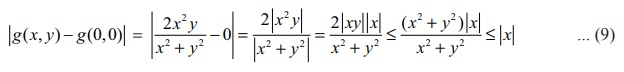
இங்கு கடைசி வரியில் நாம் 2 |xy| ≤ x2 + y2 என்பதை அனைத்து x, y ∈ℝ எனப் பயன்படுத்தியுள்ளதைக் கவனிக்க. (இது 0 ≤ (x - y)2 -இலிருந்து கிடைப்பது) (x,y) → (0,0) என்பதால் |x| → 0 எனக் கிடைக்கின்றது. சமன்பாடு (9)-லிருந்து 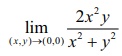  = 0 = g(0, 0) எனக்கிடைக்கின்றது. ஆகவே (0, 0) இல் g தொடர்ச்சியானது என்பது நிரூபிக்கப்படுகிறது. எனவே ℝ2 –ன்ஒவ்வொரு புள்ளியிலும் g தொடர்ச்சியானதாகும்.