பிழைகள் : தனிப்பிழை, சார்பிழை, மற்றும் சதவீத பிழை (Errors: Absolute Error, Relative Error and Percentage Error)

பிழைகள் : தனிப்பிழை, சார்பிழை, மற்றும் சதவீத பிழை (Errors: Absolute Error, Relative Error and Percentage Error) 

நாம் ஒரு மதிப்பைத் தோராயப்படுத்தும்போது அங்கு பிழை ஏற்படுகின்றது. இந்தப் பிரிவில், சமன்பாடு (4) ஆல் நேரியல் தோராய மதிப்பு மூலம் ஏற்படும் பிழையைக் கருத்தில் கொள்வோம். பிழைகளின் பல வகைகளைப் பற்றியும் காண்போம். h = x – x0 என எடுக்க, x = x0 + h எனகிடைக்கும். இதனால் சமன்பாடு (5)

 E(h) = f (x0 + h) - f (x0) - f'(x0)h என மாறும்.       .. (6)

E(0) = 0 என்பதைக் கவனிக்க மற்றும் x0 என்ற புள்ளியில் f -ன் தொடர்ச்சித் தன்மையினால் limh→0 E(h) = 0 என்பதை நாம் முன்பே பார்த்துள்ளோம். மேலும் f வகையிடத்தக்கது என்பதால் சமன்பாடு (1)இலிருந்து

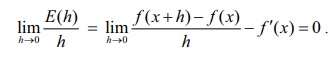
f என்ற சார்பு x0 இல் வகையிடத்தக்கது எனில், h பூச்சியத்தை நெருங்குவதைவிட, E(h) வேகமாக பூச்சியத்தை நெருங்குவதைக் காணலாம்.

வரையறை 8.2

ஒரு குறிப்பிட்ட அளவையைத் தீர்மானிக்க வேண்டும் என்க. அதன் துல்லியமான மதிப்பு மெய்மதிப்பு எனப்படும். சில நேரங்களில் நாம் அவற்றின் தோராய மதிப்பை, தோராய மதிப்பிடல் முறையில் காண்கின்றோம். இந்நிலையில்

தனிப்பிழை = மெய்மதிப்பு - தோராய மதிப்பு என வரையறுக்கப்படுகிறது.

எனவே சமன்பாடு (6) நேரியல் தோராய மதிப்பு முறையில் ஏற்படும் தனிப்பிழையைத் தருகின்றது. 

எடுத்துக்காட்டு 8.2

நேரியல் தோராய மதிப்பீட்டு முறை மூலம் √9.2 -ன் தோராய மதிப்பைக் கணிப்பான் உதவியில்லாமல் காண்க.

தீர்வு

நேரியல் தோராய மதிப்பீட்டு முறையில் √9.2 -ன் தோராய மதிப்பைக் காண வேண்டியுள்ளது. சமன்பாடு (3)-ன் படி f (x0 + ∆x) ≈ f (x0) + f (x) ∆x என உள்ளது. இதற்கு நாம் பொருத்தமான f , x0 மற்றும் ∆x ஆகியவற்றைத் தேர்வு செய்ய வேண்டும். நம்முடைய இந்தத் தேர்வு மேற்கண்ட தோராய மதிப்பு சமன்பாட்டின் வலப்பக்கத்தை கணிப்பான் உதவியில்லாமல் கணக்கிடக்கூடிய வகையில் இருக்கவேண்டும். எனவே

f (x) = √x, x0 = 9 மற்றும் ∆x = 0.2 என நாம் தேர்வு செய்வோம். இதனால் f'(x0) = 1/2√9 மற்றும்

√9.2 = f (9) + f'(9)(0.2) = 3 + 0.2/6 = 3.03333 என கிடைக்கும். 

தற்போது, ஒப்பிட்டுக் பார்ப்பதற்காக, கணிப்பானைப் பயன்படுத்தினால்√9.2 = 3.03315 என கிடைப்பதைக் காணலாம். நம் தோராய மதிப்பு முதல் மூன்று தசம இடங்களுக்கு சரியாக உள்ள தைக் காணலாம். எனவே பிழை 3.03315-3.03333 = -0.00018. [மேலும் இங்கு ஒருவர் f (x) = √1 + x, x0 = 8 மற்றும் ∆x = 0.2 எனவும் தேர்வு செய்யலாம். எனவே f மற்றும் x0 -ன் தேர்வு தனித்தன்மையுடையதாக இருக்க வேண்டியதில்லை].

எனவே மேற்கண்ட எடுத்துக்காட்டில் தனிப்பிழை என்பது 3.03315 - 3.03333 = -0.00018. தனிப்பிழை எந்த அளவு பிழை என்பதைக் குறிக்கின்றது; ஆனால் அது தோராய மதிப்பு எந்த அளவுக்கு மெய்மதிப்பிற்கு அருகாமையில் நன்றாக உள்ளது என்பதைக் கூறாது. இதற்காக இரண்டு எளிய நிலைகளைக் காணலாம்.

நிலை 1 : ஏதோ ஒரு அளவின் மெய்மதிப்பு 5 மற்றும் தோராய மதிப்பு 4 என்க. அதன் தனிப்பிழை 5- 4 = 1

நிலை 2 : ஏதோ ஒன்றின் மெய்மதிப்பு 100 மற்றும் தோராய மதிப்பு 95 என்க. தற்போது அதன் தனிப்பிழை 100 - 95 = 5. எனவே முதல் நிலையின் தனிப்பிழை இரண்டாம் நிலையை விடக்குறைவாக உள்ளது.

இந்த இரு தோராய மதிப்புகளில் எது சிறந்த தோராய மதிப்பு மற்றும் ஏன்? ஒரு தோராய மதிப்பு சிறந்ததா இல்லையா என்பது பற்றி தனிப்பிழை சரியாக தெரிவிப்பதில்லை. அதே சமயம் சார்பிழை அல்லது சதவீதப்பிழை (கீழே வரையறுக்கப்பட்டுள்ளது), கணக்கிடுவோமானால் அந்த தோராய மதிப்பு எவ்வளவு சிறந்தது என்பதைக் காணலாம். மெய்மதிப்பு பூச்சியம் எனில் நம் தோராய மதிப்பு மெய்மதிப்புக்கு எந்த அளவிற்கு நெருக்கமாக உள்ளது என்பது நமக்குத் தெரியும். மெய்மதிப்பு பூச்சியமில்லை எனில் அதைப் பின்வருமாறு வரையறுப்போம். 

வரையறை 8.3 

மெய்மதிப்பு பூச்சியமற்றது எனில்

சார்பிழை = மெய்மதிப்பு - தோராய மதிப்பு / மெய்மதிப்பு 

சதவீதப்பிழை = சார்பிழை × 100.

குறிப்பு: தனிப்பிழை அளவீட்டிற்கு அலகு உண்டு. அதே சமயம் சார்பிழை, சதவீதப் பிழை ஆகியவற்றிற்கு அலகுகள் இல்லை .

மேற்கண்ட நிலைகளில்

முதல் நிலை : சார்பிழை = 1/5 = 0.2; சதவீதப் பிழை = 1/5 × 100 = 20%

 இரண்டாம் நிலை : சார்பிழை = 5/100; சதவீதப் பிழை = 5/100 × 100 = 5%.

இதிலிருந்து இரண்டாவது தோராய மதிப்பு முதல் தோராய மதிப்பீட்டை விடச் சிறந்தது. சார்பிழை அல்லது சதவீதப் பிழைகணக்கிட எதன் தோராய மதிப்பைக் கணக்கிடுகின்றோமோ அதன் மெய்மதிப்பு தெரிந்திருக்க வேண்டும் என்பதைக் கவனிக்கவும்.

மேலும் சில எடுத்துக்காட்டுகளைக் காணலாம். 

எடுத்துக்காட்டு 8.3

ஒரு சோப்பு நுரையின் வடிவம் கோளமாக உள்ளது என எடுத்துக் கொள்வோம். ஆரம் 5 செமீஇலிருந்து 5.2 செமீ-ஆக மாறும் போது ஏற்படும் வளைபரப்பின் தோராய அதிகரிப்பை நேரியல் தோராய மதிப்பு முறையில் காண்க. மேலும் அதன் சதவீதப் பிழையையும் காண்க. 

தீர்வு

ஆரம் r உள்ள கோளத்தின் வளைபரப்பு S(r) = 4πr2 என்பதை நினைவுகூர்க. நம்மால் சூத்திரத்தைப் பயன்படுத்தி சரியான மாற்றத்தைக் கணக்கிட முடியும் என்றாலும் நேரியல் தோராய மதிப்பு முறையைப் பயன்படுத்தி தோராய மதிப்பைக் காணலாம். சமன்பாடு (4)-ன்படி 

வளைபரப்பின் தோராய மாற்றம் = S(5.2) - S(5) ≈ S'(5)(0.2)

 = 8π (5)(0.2)

 = 8π செமீ2

சரியான கணக்கீட்டின்படி வளைபரப்பின் மாற்றம் 

S(5.2) - S(5) = 108.16π -100π = 8.16 செமீ2

சதவீதப் பிழை = சார்பிழை × 100 = 8.16 π - 8 π / 8.16π × 100 = 1.9607%

எடுத்துக்காட்டு 8.4

ஒரு நேர்வட்ட உருளையின் ஆரம் r =10 செமீ மற்றும் உயரம் h = 20 செமீ. உருளையின் ஆரம் 10 செமீ இலிருந்து 10.1 செமீ-ஆக அதிகரிக்கின்றது என்க. மேலும் உயரம் மாறாமல் உள்ளது எனில் உருளையின் கன அளவில் ஏற்படும் மாற்றத்தைக் கணக்கிடுக. மேலும் அதன் சார்பிழை மற்றும் சதவீதப் பிழையையும் காண்க.

தீர்வு

உருளையின் கன அளவு V = πr2h என்பதை நினைவு கூர்வோம், இங்கு ஆரம் r மற்றும் உயரம் h ஆகும். V (r) = πr2h = 20πr2

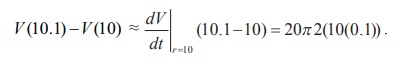
எனவே கன அளவில் ஏற்படும் மாற்றத்தின் மதிப்பு 40 π செமீ3 கன அளவில் ஏற்படும் துல்லியமான மாற்றம்

V (10.1) - V (10) = 2040.2 π - 2000π = 40.2 π செமீ3. 

எனவே சார்பிழை = 40.2π  - 40 π / 40.2 π = 1/201 = 0.00497; 

மற்றும் சதவீதப் பிழை = சார்பிழை × 100 = 1/ 201 × 100 = 0.497%.