ஒன்றின் n−ஆம் படிமூலங்கள் (The nth roots of unity)

3. ஒன்றின் n−ஆம் படிமூலங்கள் (The nth roots of unity)

 z" =1, n ஒரு முழு எண், என்ற சமன்பாட்டின் தீர்வுகளே ஒன்றின் n −ஆம் படிமூலங்கள் ஆகும். 

 z =1 என்ற சமன்பாட்டை துருவ வடிவில் z = cos(0 + 2kπ) + i sin (0 + 2kπ) = ei2kπ , k = 0, 1, 2,...  டி மாய்வரின் தேற்றத்தைப் பயன்படுத்தி ஒன்றின் n −ஆம் படிமூலங்களை பின்வருமாறு காணலாம்:

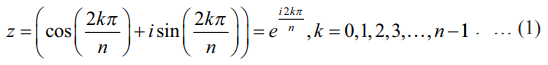
கொடுக்கப்பட்ட மிகை முழு எண் n −க்கு, z என்பது ஒன்றின் n−ஆம் படி மூலமாக இருக்குமெனில் zn = 1 என இருக்க வேண்டும்.

இதனை ω என்ற கலப்பெண்ணின் மூலம் குறித்தால்,

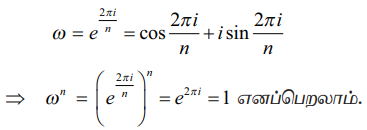
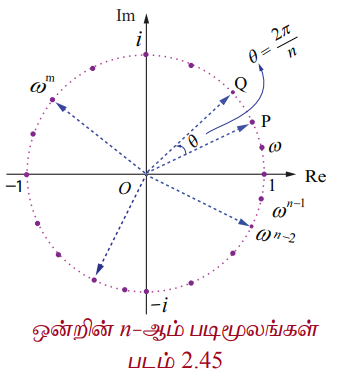
ஆகவே ஒன்றின் n−ஆம் படிமூலங்களில் ஒன்று ω ஆகும். சமன்பாடு (1)−லிருந்து 1, ω, ω2, .... , ωn−1 ஆகியவை ஒன்றின் n−ஆம் படிமூலங்கள் ஆகும். 1, ω, ω2, .... , ωn−1 என்ற இந்த கலப்பெண்கள் கலப்பெண் தளத்தில் n பக்கங்களை உடைய சீரான பலகோணத்தின் உச்சிப்புள்ளிகளாக ஓரலகு வட்டத்தின் மீது படத்தில் காட்டியுள்ளவாறு அமையும். இந்த எல்லா n−ஆம் படிமூலங்களின் மட்டு மதிப்புகளும் 1 எனவே இவை ஆதியை மையமாகவும் ஆரம் 1 கொண்ட வட்டத்தின் மீது அமையும். மேலும் இந்த n மூலங்களில் அடுத்தடுத்த மூலக்ளுக்கு இடைப்பட்ட கோண வித்தியாசம் 2π/n. எனவே, n மூலங்களும் வட்டத்தின் மீது சீரான இடைவெளி விட்டு அமையும்.

ஒன்றின் n −ஆம் படிமூலங்கள் 1, ω, ω2, .... , ωn−1 ஆகியவை ω −வை பொது விகிதமாகக் கொண்ட பெருக்குத் தொடரை அமைக்கிறது.

ஆகவே 1 + ω + ω2 + .... + ωn−1 = [1 − ωn] / [1 – ω] = 0 இங்கு ωn  = 1 மற்றும் ω ≠ 1

ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தின் கூட்டுத்தொகை 1 + ω + ω2 + .... + ωn−1 = 0 ஆகும்.

ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தின் பெருக்குத் தொகை

1 ω ω2 ....  ωn−1 = ω0+1+2+3+…+(n−1) = ω [(n−1)n] /2

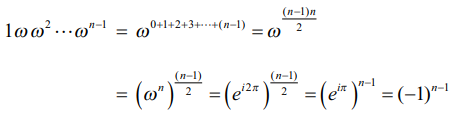
ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தின் பெருக்குத்தொகை

1ωω2....  ωn−1 = (−1)n−1 ஆகும்.

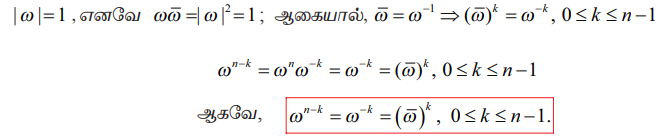
குறிப்பு

(1) ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தும் பெருக்குத் தொடரை அமைக்கின்றது.

(2) ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தின் கூட்டுத்தொகை பூஜ்ஜியமாகும்.

(3) ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தின் பெருக்குத்தொகை (−1)n−1 ஆகும்.

(4) ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தும் ஆதியை மையமாகவும் ஆரம் 1 கொண்ட வட்டத்தின் மீது அமைவதுடன் வட்டத்தை n சமபாகங்களாகப் பிரிக்கின்றது. மேலும் இவை n பக்கங்கள் கொண்ட பலகோணத்தை அமைக்கின்றது.

எடுத்துக்காட்டு 2.32

ஒன்றின் மூன்றாம் படிமூலங்களைக் காண்க.

தீர்வு

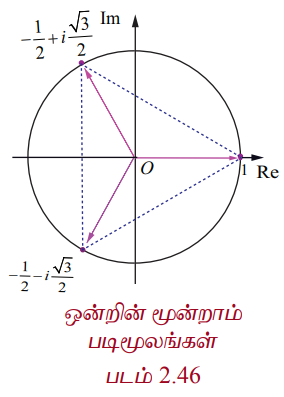
நாம் 11/3 ஐ காணவேண்டும். z = 11/3 எனில், z3 = 1 ஆகும். 

z3 =1 என்ற சமன்பாட்டை துருவ வடிவில் எழுத

z3 = cos(0 + 2kπ) + isin (0 + 2kπ) = ei2kπ, k = 0, 1, 2,...

எனவே, z = cos(2kπ/3) + isin (2kπ/3) = ei [2kπ / 3] , k = 0, 1, 2.

k = 0, 1, 2 எனப்பிரதியிட

k = 0, z = cos 0 + i sin 0 = 1.

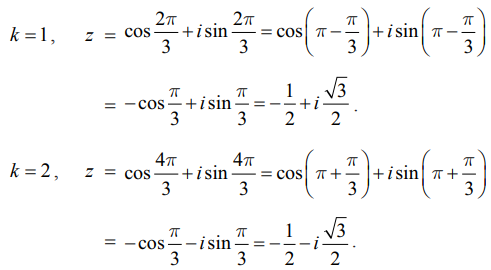
ஆகவே, ஒன்றின் மூன்றாம் படிமூலங்கள்

1, [−1 + i√3] / 2 , [ −1− i√3] / 2 ⇒ 1, ω , மற்றும் ω2 இங்கு ω = ei (2π/3) = [−1 + i√3] / 2. 

எடுத்துக்காட்டு 2.33

ஒன்றின் நான்காம் படிமூலங்களைக் காண்க.

தீர்வு

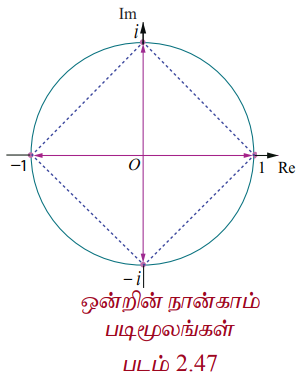
நாம் 11/4 ஐ காண வேண்டும். z = 11/4 எனில் z4 = 1 ஆகும். 

z4 = 1 என்ற சமன்பாட்டை துருவ வடிவில் எழுத,

z = cos(0 + 2kπ) + isin (0 + 2kπ) =   ei2kπ ‚k = 0, 1, 2, ...

எனவே, 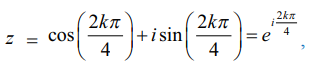k = 0, 1, 2, 3

k = 0, 1, 2, 3 எனப்பிரதியிட

k = 0,   z = cos 0 + i sin0 = 1.

k = 1,    z = cos(π/2) + isin (π/2) = i.

k = 2,    z = cos π + isin π = −1.

k = 3,    z = cos(3π/2) + isin (3π/2) =  − cos(π/2) − isin (π/2) = − i

ஒன்றின் நான்காம் படிமூலங்கள் 1, i, − 1, − i ⇒ 1, ω , ω2 மற்றும் ω3 இங்கு ω = ei [2π/4]  = i .

குறிப்பு

(i) இப்பாடப்பகுதியில் ω என்பது ஒன்றின் n −ஆம்படிமூலத்தை குறிப்பிடப் பயன்படுத்தப்பட்டுள்ளது. எனவே ω ஆனது n −ஐப் பொருத்து எவ்வாறு அமைகின்றது என்பது அட்டவணைப்படுத்தப்பட்டுள்ளது.

(ii) zeiθ என்பது z −ஐ ஆதியை பொறுத்து θ கோணம் கடிகார எதிர்திசையில் சுற்றுவது ஆகும்.

எடுத்துக்காட்டு 2.34

z3 + 8i = 0 என்ற சமன்பாட்டைத் தீர்க்க. இங்கு z ∈ ℂ.

தீர்வு

z3 + 8i = 0 என்க.

⇒ z3 =  −8i

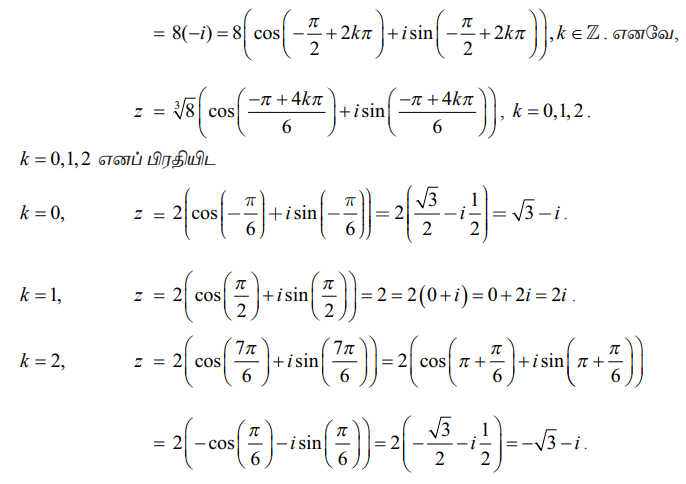
z −ன் மதிப்புகள் √3 − i, 2i, மற்றும் −√3 − i.

எடுத்துக்காட்டு 2.35

√3 + i −ன் எல்லா மூன்றாம் படிமூலங்களையும் காண்க.

தீர்வு

நாம் (√3 + i)1/3 −ன் மதிப்புகளை காண வேண்டும். z = (√3 + i)1/3 எனில்

z3 = 3 + i = r(cos θ + isin θ)  ஆகும்.

r = √[3 + 1] = 2, மற்றும் α = θ = π/6    (√3 + i  I கால்பகுதியில் அமைவதால்)

ஆகவே, 

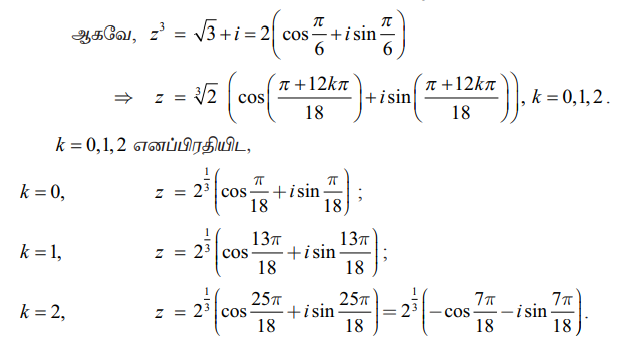
எடுத்துக்காட்டு 2.36

z1, z2, மற்றும் z3 ஆகியவை |z| = 2 என்ற வட்டத்தின் மீதமைந்த சமபக்க முக்கோணத்தின் உச்சிப்புள்ளிகள் என்க. மேலும் z1 = 1 + i√3 எனில், z2 மற்றும் z3 −ஐக் காண்க.

தீர்வு

|z| = 2 என்பது (0,0) −வை மையமாகவும். 2 ஐ ஆரமாகவும் கொண்ட வட்டத்தைக் குறிக்கும். A, B, மற்றும் C ஆகியவை முக்கோணத்தின் முனைப்புள்ளிகள் என்க. z1, z2 மற்றும் z3 ஆகியவை |z| = 2 என்ற வட்டத்தின் மீதமைந்த சமபக்க முக்கோணத்தின் உச்சிப்புள்ளிகள். எனவே, AB, BC, மற்றும் CA என்ற பக்கங்கள் ஆதியை பொருத்து (முக்கோணத்தின் சுற்று வட்ட மையம்) 2π/3 ரேடியன்கள் (120°) கோண இடைவெளி விட்டு அமையும். (zeiθ என்பது z −ஐ ஆதியைப் பொருத்து θ கோணம் கடிகார எதிர்திசையில் சுற்றுவது ஆகும்)

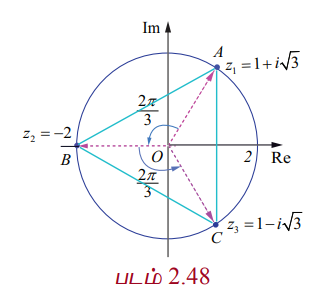
ஆகவே, z1 −ஐ முறையே 2π/3 மற்றும் 4π/3 கோணங்கள் சுற்றுவதால் z2 மற்றும் z3 ஆகியவற்றை பெறலாம்.

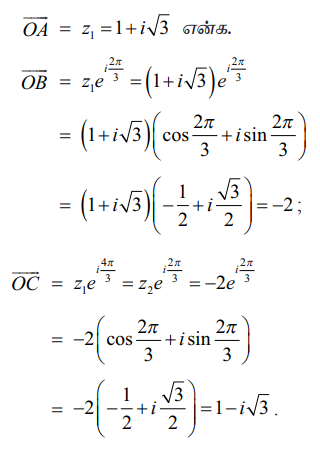
ஆகவே, z2 = −2 and z3 = 1 − i√3