டி மாய்வரின் தேற்றமும் அதன் பயன்பாடுகளும் (de Moivre's Theorem and its Applications)

டி மாய்வரின் தேற்றமும் அதன் பயன்பாடுகளும் (de Moivre's Theorem and its Applications)

டி மாய்வர் (1667 – 1754)

ஆபரகாம் டி மாய்வர் (1667 − 1754) என்ற கணிதவியல் அறிஞர் முக்கோணவியலில் கலப்பு எண்களைப் பயன்படுத்தினார்.

(cos θ + isin θ)n = (cos nθ + isin nθ) எனும் சூத்திரம் அவரது பெயரால் அறியப்படுகின்றது.

முக்கோணவியலை வடிவியலின் ஆதிக்கத்தில் இருந்து மீட்டெடுத்து பகுப்பாய்விற்குள் கொண்டு செல்ல அவர் பெயரால் வழங்கும் இச்சூத்திரமே தூண்டுகோலாக அமைந்தது.

1. டி மாய்வரின் தேற்றம் (de Moivre's Theorem)

டி மாய்வரின் தேற்றம்

கொடுக்கப்பட்ட கலப்பெண் cos θ + isin θ மற்றும் n என்ற முழு எண்ணிற்கு (cos θ + isin θ)n = (cos nθ + isin nθ)

கிளைத்தேற்றம்

(1) (cos θ − isin θ)n = cos nθ − isin nθ

(2) (cos θ + isin θ)−n = (cos nθ − isin nθ)

(3) (cos θ − isin θ)−n = cos nθ + isin nθ

(4) sin θ + i cos θ = i (cos θ − isin θ).

நாம் இப்பொழுது டிமாய்வரின் தேற்றத்தை கலப்பெண்களை சுருக்குதல் மற்றும் சமன்பாடுகளைத் தீர்த்தல் போன்றவற்றிற்கு பயன்படுத்துவோம்.

எடுத்துக்காட்டு 2.28

z = (cos θ + isin θ) எனில், zn + 1/zn = 2 cos nθ மற்றும் zn − 1/zn = 2isin nθ என நிறுவுக.

தீர்வு

z = (cos θ + isin θ) என்க

டி மாய்வரின் தேற்றப்படி

zn = (cos θ + isin θ)n = (cos nθ + isin nθ)

1/zn = z−n = cos nθ − isin nθ

ஆகவே, zn + 1/zn = (cos nθ + isin nθ) + (cos nθ − isin nθ)

zn + 1/zn = 2 cos nθ

இதுபோலவே,

zn − 1/zn = (cos nθ + isin nθ) − (cos nθ − isin nθ)

zn − 1/zn = 2 isin nθ

எடுத்துக்காட்டு 2.29

சுருக்குக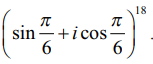

தீர்வு

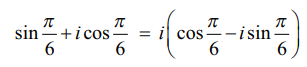ஆக எழுதலாம்.

இருபுறமும் 18−ன் அடுக்கிற்கு உயர்த்த,

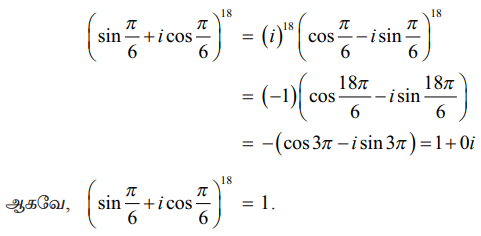
எடுத்துக்காட்டு 2.30

சுருக்குக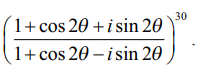

தீர்வு

z = cos 2θ + isin 2θ என்க

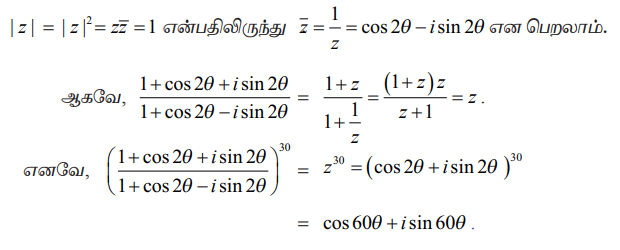
= cos 60θ + isin 60θ .

எடுத்துக்காட்டு 2.31

சுருக்குக (i) (1 + i)l8

(ii) (−√3 + 3i)31

தீர்வு

(i) (1 + i)l8

1 + i = r (cos θ + isin θ) என்க

r = √[12 + 12 ] = √2 ; α = tan−1[1/1] = π/4 ,

θ  = α = π/4      (∵ 1 + i ஆனது முதலாம் கால் பகுதியில் உள்ளதால்)

ஆகவே, 1 + i = √2 ( cos π/4  + isin π/4 )

இருபுறமும் 18−ன் அடுக்கிற்கு உயர்த்த,

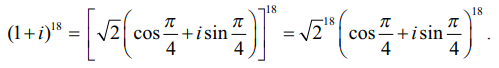
டி மாய்வரின் தேற்றப்படி,

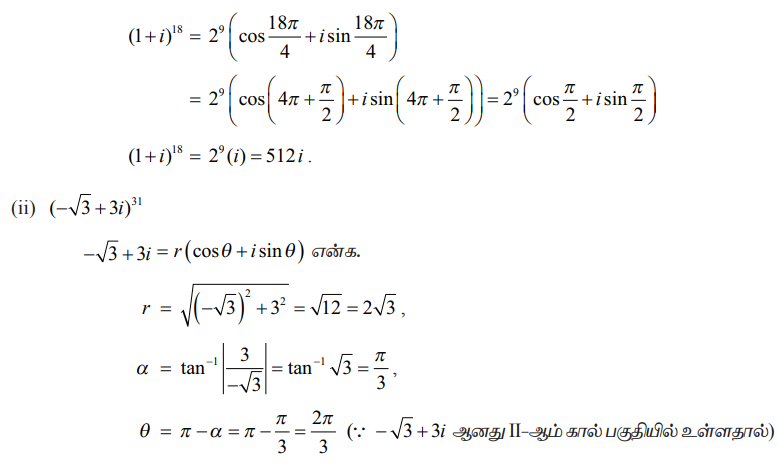
θ = π – α = π – π/3 = 2π/3 (∵−√3 + 3i ஆனது II−ஆம் கால் பகுதியில் உள்ளதால்) 

ஆகவே, −√3 + 3i = 2√3 (cos 2π/3  + isin 2π/3)

இருபுறமும் 31−ன் அடுக்கிற்கு உயர்த்த,

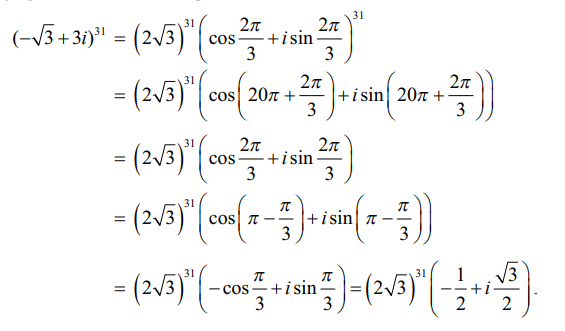
2. ஒரு கலப்பெண்ணின் n−ஆம் படிமூலங்களைக் காணல் (Finding nth roots of a complex number)

கலப்பெண்களின் மூலங்களைக் காண டி மாய்வரின் சூத்திரத்தைப் பயன்படுத்துகிறோம். n ஒரு முழு எண் மற்றும் ω ஒரு கலப்பெண் ஆனது z−ன் n −ஆம் படிமூலம் z1/n எனக்கொண்டால்

ωn = z எனப்பெறலாம்.          …………….(1)

ω = ρ(cos ∅ + i sin∅)

மேலும் z = r(cos θ + isin θ) = r(cos(θ + 2kπ) + isin(θ + 2kπ))  , k ∈ ℤ என்க.

z −ன் n−ஆம் படிமூலம் ω எனில்

ωn = z 

⇒ ρn (cos ∅ + i sin∅) n  = r(cos(θ + 2kπ) + i sin (θ + 2kπ)), k ∈ ℤ

டி மாய்வரின் தேற்றப்படி,

ρn (cos n∅ + i sin n∅) =  r(cos(θ + 2kπ) + i sin (θ + 2kπ)), k ∈ ℤ 

மட்டுக்களையும் வீச்சுகளையும் சமப்படுத்த

ρn = r மற்றும் n∅ = θ + 2kπ , k ∈ ℤ எனப்பெறலாம்.          

ρ = r1/n மற்றும் ∅ = (θ + 2kπ) / n , k ∈ ℤ 

ஆகவே. ω −ன் மதிப்புகள்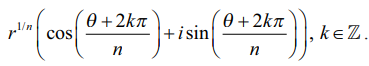

k −விற்கு எண்ணிக்கையற்ற மதிப்புகள் இருந்தாலும் ω −விற்கு வெவ்வேறான மதிப்புகளைப் பெற k = 0, 1, 2, 3, ..., n − 1 எனப்பிரதியிட வேண்டும். k = n, n + 1, n + 2, ... என பிரதியிட்டால் கிடைத்த மூலங்களே (சுற்றுவட்ட முறையில்) சீரான இடைவெளியில் கிடைக்கும். ஆகவே  z = r(cos θ + isin θ)  என்ற கலப்பெண்ணின் n−ஆம் படிமூலங்கள்

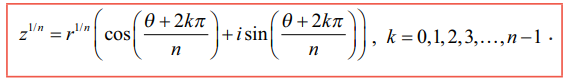
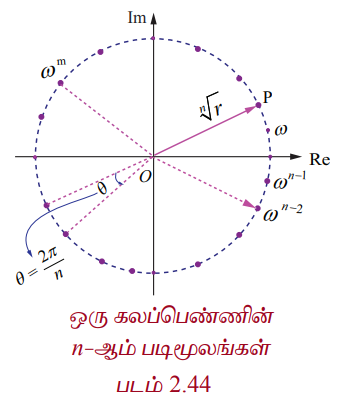
ஒரு கலப்பெண்ணின் n−ஆம் மூலத்தினை 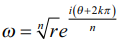எனக்கொள்வதன் மூலமும் படத்தில் காட்டியுள்ளது போன்ற ஒரு அழகிய வடிவியல் விளக்கத்தினைப் பெறலாம். இந்த n மூலங்களுக்கும், | ω | = n√r அதாவது மட்டு மதிப்பு n√r எனவே இவை ஆதியை மையமாக n√r ஆரமுள்ள வட்டத்தின் மீது அமையும். மேலும் இந்த n மூலங்களில் அடுத்தடுத்த மூலங்களின் வீச்சுகள் 2π/n என்ற வித்தியாசத்தில் வேறுபடுவதால் இந்த n மூலங்களும் வட்டத்தின் மேல் சீரான இடைவெளிகளில் அமையும். 

மேற்குறிப்பு

(1) டி மாய்வர் தேற்றத்தின் பொது வடிவம் (General form of de Moivre's Theorem)

x ஒரு விகிதமுறு எண் எனில் cos xθ + isin xθ என்பது (cos θ + isin θ)x −ன் மதிப்புகளில் ஒன்றாகும்.

(2) அலகு வட்டத்தின் துருவ வடிவம் (Polar form of unit circle)

z = eiθ = cos θ + isin θ என்க.

எனவே, |z|2 = | cos θ + isin θ |2 எனப்பெறலாம்.

⇒ |x + iy|2 = cos2 θ + sin2 θ = 1

⇒ x2 + y2 = 1.

எனவே, |z| = 1 ஆனது ஆதியை மையமாகக் கொண்ட அலகு வட்டத்தை (ஓரலகு வட்டத்தை) குறிக்கிறது.

3. ஒன்றின் n−ஆம் படிமூலங்கள் (The nth roots of unity)

 z" =1, n ஒரு முழு எண், என்ற சமன்பாட்டின் தீர்வுகளே ஒன்றின் n −ஆம் படிமூலங்கள் ஆகும். 

 z =1 என்ற சமன்பாட்டை துருவ வடிவில் z = cos(0 + 2kπ) + i sin (0 + 2kπ) = ei2kπ , k = 0, 1, 2,...  டி மாய்வரின் தேற்றத்தைப் பயன்படுத்தி ஒன்றின் n −ஆம் படிமூலங்களை பின்வருமாறு காணலாம்:

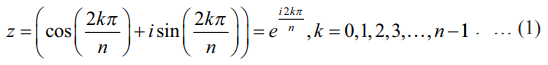
கொடுக்கப்பட்ட மிகை முழு எண் n −க்கு, z என்பது ஒன்றின் n−ஆம் படி மூலமாக இருக்குமெனில் zn = 1 என இருக்க வேண்டும்.

இதனை ω என்ற கலப்பெண்ணின் மூலம் குறித்தால்,

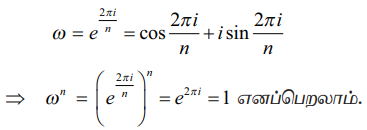
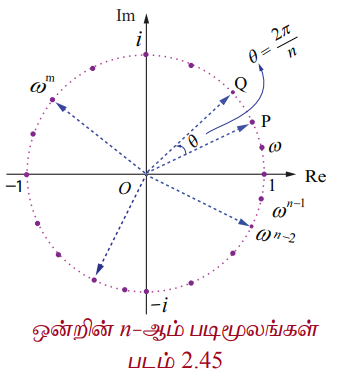
ஆகவே ஒன்றின் n−ஆம் படிமூலங்களில் ஒன்று ω ஆகும். சமன்பாடு (1)−லிருந்து 1, ω, ω2, .... , ωn−1 ஆகியவை ஒன்றின் n−ஆம் படிமூலங்கள் ஆகும். 1, ω, ω2, .... , ωn−1 என்ற இந்த கலப்பெண்கள் கலப்பெண் தளத்தில் n பக்கங்களை உடைய சீரான பலகோணத்தின் உச்சிப்புள்ளிகளாக ஓரலகு வட்டத்தின் மீது படத்தில் காட்டியுள்ளவாறு அமையும். இந்த எல்லா n−ஆம் படிமூலங்களின் மட்டு மதிப்புகளும் 1 எனவே இவை ஆதியை மையமாகவும் ஆரம் 1 கொண்ட வட்டத்தின் மீது அமையும். மேலும் இந்த n மூலங்களில் அடுத்தடுத்த மூலக்ளுக்கு இடைப்பட்ட கோண வித்தியாசம் 2π/n. எனவே, n மூலங்களும் வட்டத்தின் மீது சீரான இடைவெளி விட்டு அமையும்.

ஒன்றின் n −ஆம் படிமூலங்கள் 1, ω, ω2, .... , ωn−1 ஆகியவை ω −வை பொது விகிதமாகக் கொண்ட பெருக்குத் தொடரை அமைக்கிறது.

ஆகவே 1 + ω + ω2 + .... + ωn−1 = [1 − ωn] / [1 – ω] = 0 இங்கு ωn  = 1 மற்றும் ω ≠ 1

ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தின் கூட்டுத்தொகை 1 + ω + ω2 + .... + ωn−1 = 0 ஆகும்.

ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தின் பெருக்குத் தொகை

1 ω ω2 ....  ωn−1 = ω0+1+2+3+…+(n−1) = ω [(n−1)n] /2

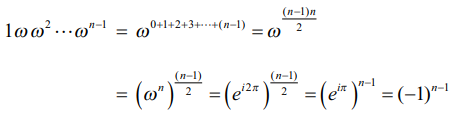
ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தின் பெருக்குத்தொகை

1ωω2....  ωn−1 = (−1)n−1 ஆகும்.

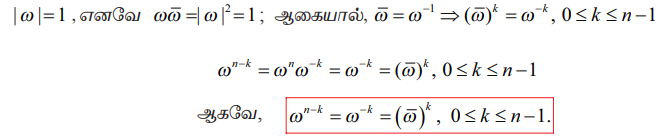
குறிப்பு

(1) ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தும் பெருக்குத் தொடரை அமைக்கின்றது.

(2) ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தின் கூட்டுத்தொகை பூஜ்ஜியமாகும்.

(3) ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தின் பெருக்குத்தொகை (−1)n−1 ஆகும்.

(4) ஒன்றின் n−ஆம் படிமூலங்கள் அனைத்தும் ஆதியை மையமாகவும் ஆரம் 1 கொண்ட வட்டத்தின் மீது அமைவதுடன் வட்டத்தை n சமபாகங்களாகப் பிரிக்கின்றது. மேலும் இவை n பக்கங்கள் கொண்ட பலகோணத்தை அமைக்கின்றது.

எடுத்துக்காட்டு 2.32

ஒன்றின் மூன்றாம் படிமூலங்களைக் காண்க.

தீர்வு

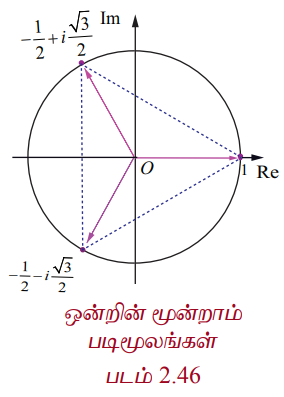
நாம் 11/3 ஐ காணவேண்டும். z = 11/3 எனில், z3 = 1 ஆகும். 

z3 =1 என்ற சமன்பாட்டை துருவ வடிவில் எழுத

z3 = cos(0 + 2kπ) + isin (0 + 2kπ) = ei2kπ, k = 0, 1, 2,...

எனவே, z = cos(2kπ/3) + isin (2kπ/3) = ei [2kπ / 3] , k = 0, 1, 2.

k = 0, 1, 2 எனப்பிரதியிட

k = 0, z = cos 0 + i sin 0 = 1.

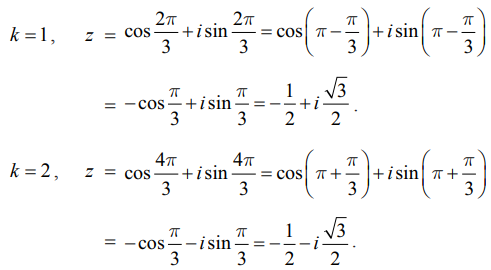
ஆகவே, ஒன்றின் மூன்றாம் படிமூலங்கள்

1, [−1 + i√3] / 2 , [ −1− i√3] / 2 ⇒ 1, ω , மற்றும் ω2 இங்கு ω = ei (2π/3) = [−1 + i√3] / 2. 

எடுத்துக்காட்டு 2.33

ஒன்றின் நான்காம் படிமூலங்களைக் காண்க.

தீர்வு

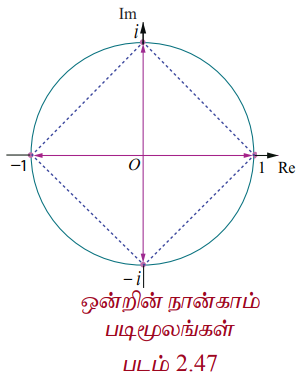
நாம் 11/4 ஐ காண வேண்டும். z = 11/4 எனில் z4 = 1 ஆகும். 

z4 = 1 என்ற சமன்பாட்டை துருவ வடிவில் எழுத,

z = cos(0 + 2kπ) + isin (0 + 2kπ) =   ei2kπ ‚k = 0, 1, 2, ...

எனவே, 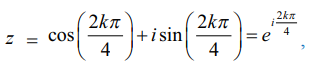k = 0, 1, 2, 3

k = 0, 1, 2, 3 எனப்பிரதியிட

k = 0,   z = cos 0 + i sin0 = 1.

k = 1,    z = cos(π/2) + isin (π/2) = i.

k = 2,    z = cos π + isin π = −1.

k = 3,    z = cos(3π/2) + isin (3π/2) =  − cos(π/2) − isin (π/2) = − i

ஒன்றின் நான்காம் படிமூலங்கள் 1, i, − 1, − i ⇒ 1, ω , ω2 மற்றும் ω3 இங்கு ω = ei [2π/4]  = i .

குறிப்பு

(i) இப்பாடப்பகுதியில் ω என்பது ஒன்றின் n −ஆம்படிமூலத்தை குறிப்பிடப் பயன்படுத்தப்பட்டுள்ளது. எனவே ω ஆனது n −ஐப் பொருத்து எவ்வாறு அமைகின்றது என்பது அட்டவணைப்படுத்தப்பட்டுள்ளது.

(ii) zeiθ என்பது z −ஐ ஆதியை பொறுத்து θ கோணம் கடிகார எதிர்திசையில் சுற்றுவது ஆகும்.

எடுத்துக்காட்டு 2.34

z3 + 8i = 0 என்ற சமன்பாட்டைத் தீர்க்க. இங்கு z ∈ ℂ.

தீர்வு

z3 + 8i = 0 என்க.

⇒ z3 =  −8i

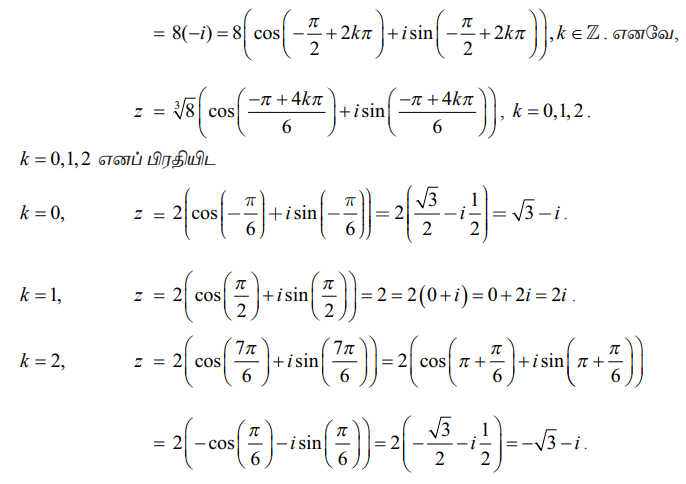
z −ன் மதிப்புகள் √3 − i, 2i, மற்றும் −√3 − i.

எடுத்துக்காட்டு 2.35

√3 + i −ன் எல்லா மூன்றாம் படிமூலங்களையும் காண்க.

தீர்வு

நாம் (√3 + i)1/3 −ன் மதிப்புகளை காண வேண்டும். z = (√3 + i)1/3 எனில்

z3 = 3 + i = r(cos θ + isin θ)  ஆகும்.

r = √[3 + 1] = 2, மற்றும் α = θ = π/6    (√3 + i  I கால்பகுதியில் அமைவதால்)

ஆகவே, 

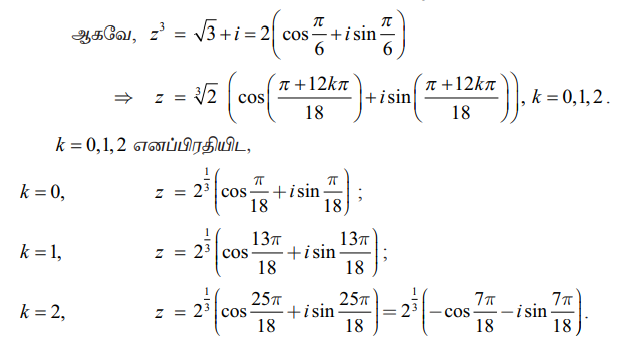
எடுத்துக்காட்டு 2.36

z1, z2, மற்றும் z3 ஆகியவை |z| = 2 என்ற வட்டத்தின் மீதமைந்த சமபக்க முக்கோணத்தின் உச்சிப்புள்ளிகள் என்க. மேலும் z1 = 1 + i√3 எனில், z2 மற்றும் z3 −ஐக் காண்க.

தீர்வு

|z| = 2 என்பது (0,0) −வை மையமாகவும். 2 ஐ ஆரமாகவும் கொண்ட வட்டத்தைக் குறிக்கும். A, B, மற்றும் C ஆகியவை முக்கோணத்தின் முனைப்புள்ளிகள் என்க. z1, z2 மற்றும் z3 ஆகியவை |z| = 2 என்ற வட்டத்தின் மீதமைந்த சமபக்க முக்கோணத்தின் உச்சிப்புள்ளிகள். எனவே, AB, BC, மற்றும் CA என்ற பக்கங்கள் ஆதியை பொருத்து (முக்கோணத்தின் சுற்று வட்ட மையம்) 2π/3 ரேடியன்கள் (120°) கோண இடைவெளி விட்டு அமையும். (zeiθ என்பது z −ஐ ஆதியைப் பொருத்து θ கோணம் கடிகார எதிர்திசையில் சுற்றுவது ஆகும்)

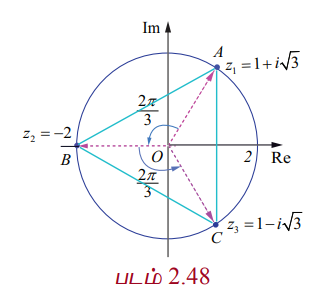
ஆகவே, z1 −ஐ முறையே 2π/3 மற்றும் 4π/3 கோணங்கள் சுற்றுவதால் z2 மற்றும் z3 ஆகியவற்றை பெறலாம்.

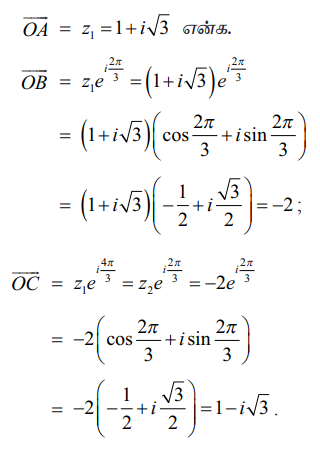
ஆகவே, z2 = −2 and z3 = 1 − i√3