கலப்பெண்ணின் ஆய்லரின் வடிவம் (Euler's Form of the complex number)

2. கலப்பெண்ணின் ஆய்லரின் வடிவம் (Euler's Form of the complex number) 

ஆய்லரின் சூத்திரம் கீழ்க்கண்டவாறு வரையறுக்கப்பட்டுள்ளது.

eiθ = cos θ + i sin θ

ஆய்லரின் சூத்திரத்திலிருந்து துருவ வடிவத்தை z = r eiθ எனப் பெறலாம்.

குறிப்பு

கலப்பெண்களின் பெருக்கம் அல்லது கலப்பெண்களின் அடுக்குகளை காணும் போது துருவ வடிவத்தை நாம் பயன்படுத்துகிறோம்.

எடுத்துக்காட்டு 2.22

பின்வரும் கலப்பெண்களுக்கு மட்டு மற்றும் முதன்மை வீச்சு ஆகியவற்றைக் காண்க.

(i) √3 + i

(ii) −√3 + i

(iii) −√3 – i

(iv) √3 − i

தீர்வு

(i) √3 + i

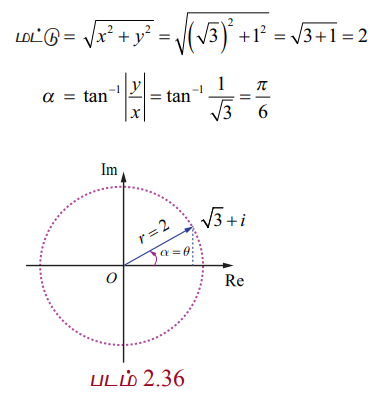
√3 + i என்ற கலப்பெண்ணானது முதல் கால் பகுதியில் அமைவதால் முதன்மை வீச்சு

θ = α = π/6

ஆகவே, √3 + i −ன் மட்டு மற்றும் முதன்மை வீச்சு முறையே 2 மற்றும் π/6 ஆகும்.

(ii) −√3 + i

மட்டு = 2 மற்றும்

α = tan−1| y/x | = tan−1 1/√3 = π/6

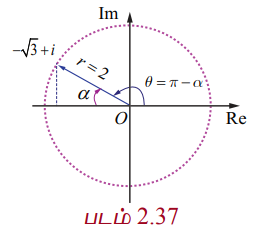
−√3 + i, என்ற கலப்பெண்ணானது இரண்டாம் கால்பகுதியில் அமைவதால் முதன்மை வீச்சு

θ = π − α = π − π/6 = 5π/6  

ஆகவே, − √3 + i −ன் மட்டு மற்றும் முதன்மை வீச்சு முறையே 2 மற்றும் 5π/6 ஆகும்.

(iii) −√3 – i

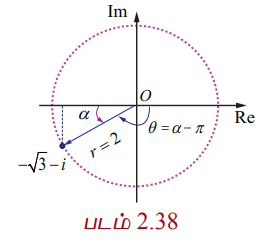
r = 2 மற்றும் α = π/6

−√3 – i என்ற கலப்பெண்ணானது மூன்றாம் கால்பகுதியில் அமைவதால் முதன்மை வீச்சு

θ = α − π =  π/6 − π = − 5π / 6  

ஆகவே, −√3 −i −ன் மட்டு மற்றும் முதன்மை வீச்சு முறையே 2 மற்றும் −5π/6 ஆகும்.

(iv) √3 – i

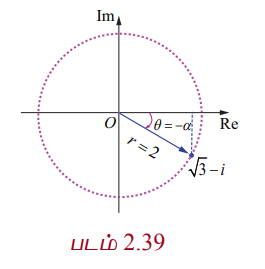
r = 2 மற்றும் α = π/6

√3 − i என்ற கலப்பெண்ணானது நான்காம் கால்பகுதியில் அமைவதால் முதன்மை வீச்சு

θ = −α =  − π/6 

ஆகவே, √3 − i  −ன் மட்டு மற்றும் முதன்மை வீச்சு முறையே 2 மற்றும் −π/6 ஆகும்.

இந்த நான்கிலும் மட்டு மதிப்புகள் சமம் ஆனால் அதன் வீச்சானது அக்கலப்பெண் அமையும் கால்பகுதியை பொருத்து அமைகின்றது.

எடுத்துக்காட்டு 2.23

(i) −1 −i 

(ii) 1 + i√3 என்ற கலப்பெண்களை துருவ வடிவில் காண்க.

தீர்வு

(i) −1− i = r(cos θ + isin θ) என்க.

 r = √[x2 + y2] = √[12 + 12] = √[1+1] = √2 மற்றும்

α = tan−1| y /x | = tan−11 = π/4 என கிடைக்கிறது.

−1− i என்ற கலப்பெண் மூன்றாம் கால்பகுதியில் அமைவதால் அதன் முதன்மை வீச்சு,

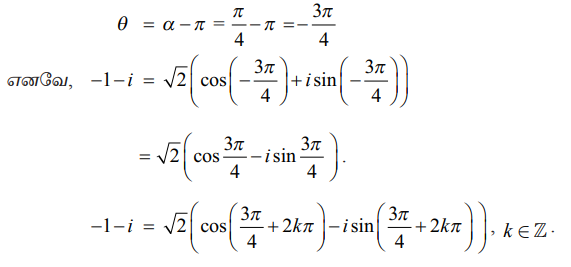
குறிப்பு

k−ன் பல்வேறு மதிப்புகளைப் பொருத்து நமக்கு பல்வேறு மாறுபட்ட துருவ வடிவங்கள் கிடைக்கும்.

(ii) 1 + i√3

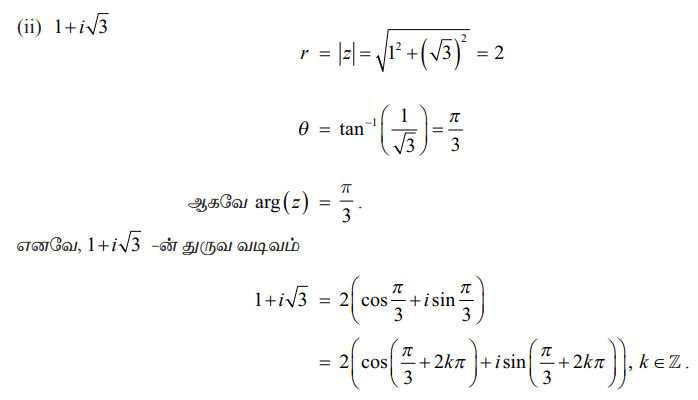
எடுத்துக்காட்டு 2.24

z = −2 / (1 + i√3) எனில் முதன்மை வீச்சு Arg z −ஐ காண்க.

தீர்வு

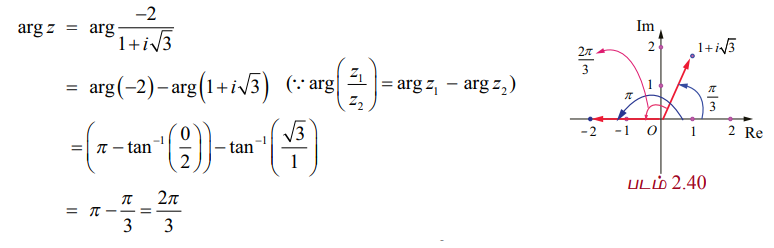
இதிலிருந்து 2π/3 என்பது arg z −ன் மதிப்புகளில் ஒன்று. 2π/3 ஆனது − π மற்றும் π −க்கு இடையில் அமைவதால் முதன்மை வீச்சு Arg z  = 2π/3 ஆகும்.

துருவ வடிவின் பண்புகள் (Properties of polar form)

பண்பு 1

z = r(cos θ + isin θ) , எனில் z−1 = 1/r (cos θ – isin θ) ஆகும்.

தீர்வு

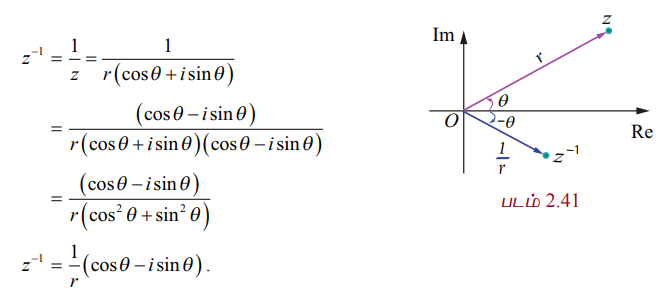
பண்பு 2

z1 = r1 (cos θ1 + isin θ1) மற்றும் z2 = r2 (cos θ2 + isin θ2) எனில், z1z2 = r1r2 (cos (θ1 + θ2)  + isin (θ1 +  θ2))

தீர்வு

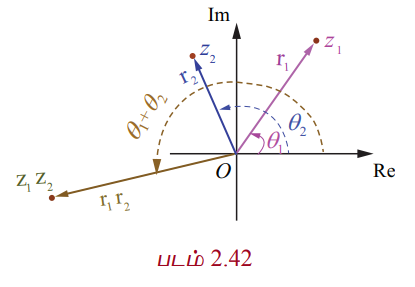
z1 = r1 (cos θ1 + isin θ1) மற்றும் 

z2 = r2 (cos θ2 + isin θ2)

⇒ z1z2 = r1 (cos θ1 + isin θ1) r2 (cos θ2 + isin θ2)

= r1r2((cos θ1 cos θ2 − sin θ1 sin θ2) + i (sin θ1 cos θ2 + sin θ2 cos θ1))

z1z2 = r1r2(cos (θ1 + θ2)  + isin (θ1 +  θ2)).

குறிப்பு

arg(z1z2) = θ1 + θ2 = arg(z1) + arg(z2)

பண்பு 3

z1 = r1 (cos θ1 + isin θ1) மற்றும் z2 = r2 (cos θ2 + isin θ2) எனில், z1/z2 = r1/r2 [cos (θ1 − θ2)  + isin (θ1 −  θ2)] 

தீர்வு

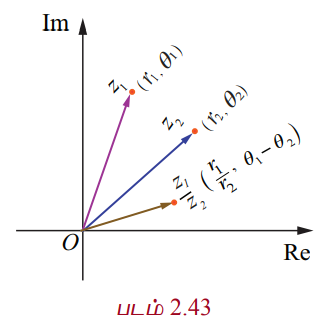
z1 மற்றும் z2 வின் துருவ வடிவங்களைப் பயன்படுத்த

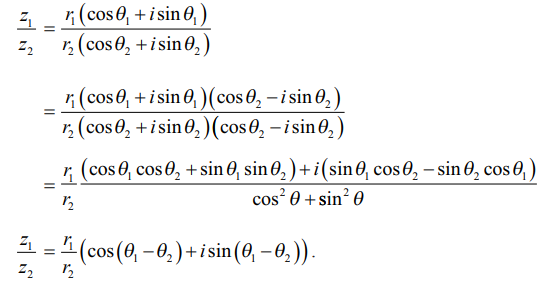
குறிப்பு

arg(z1/z2) = θ1 − θ2 = arg(z1) − arg(z2)

எடுத்துக்காட்டு 2.25

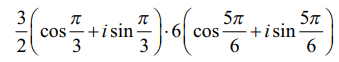என்ற பெருக்கத்தின் மதிப்பினை செவ்வக வடிவில் காண்க.

தீர்வு

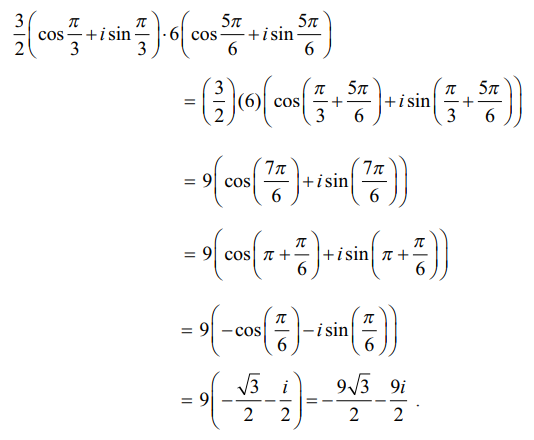
இது செவ்வக வடிவில் உள்ளது.

எடுத்துக்காட்டு 2.26

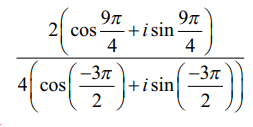என்ற வகுத்தலின் மதிப்பினை செவ்வக வடிவில் காண்க.

தீர்வு

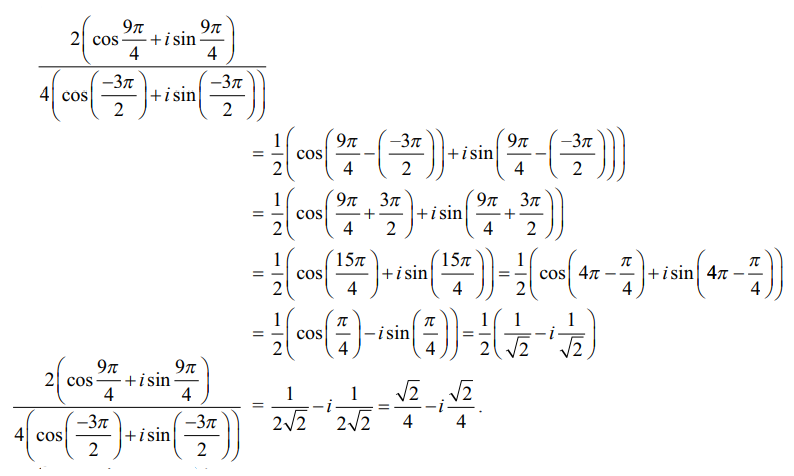
இது செவ்வக வடிவில் உள்ளது.

எடுத்துக்காட்டு 2.27

z = x + iy மற்றும் arg[(z −1)/(z + 1)] = π/2 எனில், x2 + y2 = 1 எனக்காட்டுக.

தீர்வு

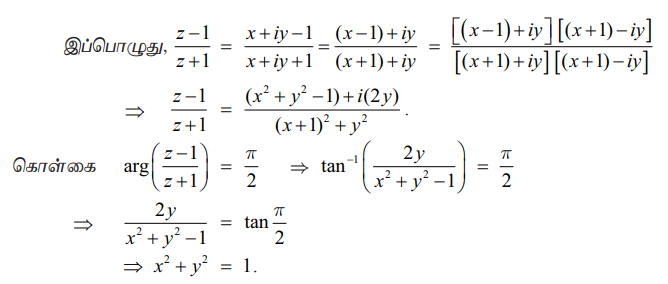
⇒ x2 + y2 = 1