கலப்பு எண்கள் (Complex Numbers)

கலப்பு எண்கள் (Complex Numbers)

நாம், x2 + 1 = 0 என்ற சமன்பாட்டிற்கு மெய்யெண் தொகுப்பில் தீர்வு இல்லை என்பதை கண்டோம். பொதுவாக, மெய் தீர்வுகள் இல்லாத மெய் எண் குணகங்களை கொண்ட பல்லுறுப்புக் கோவைச் சமன்பாடுகள் பல உள்ளன. இவ்வாறான பல்லுறுப்புக் கோவைச் சமன்பாடுகளின் தீர்வுகளை உள்ளடக்க மெய் எண் தொகுப்பானது விரிவுபடுத்தப்படுகின்றது. இக்காரணத்திற்காக கணிதவியல் அறிஞர்கள் கலப்பெண்கள் என்ற எண்களின் தொகுப்பை வரையறுக்கத் தூண்டப்பட்டனர்.

இப்பகுதியில் நாம் கீழ்காண்பவைகளை வரையறுப்போம்.

(i) செவ்வக வடிவில் கலப்பெண்கள்

(ii) துருவ வடிவம்

(iii) கலப்பெண்களின் மீதான இயற்கணிதச் செயல்பாடுகள்

கலப்பெண்கள் தொகுப்பு என்பது கற்பனை அலகு i கொண்டு விரிவாக்கம் செய்யப்பட்ட மெய் எண் தொகுப்பின் விரிவாக்கமாகும்.

மெய் எண்கள் x மற்றும் y, i2 = −1 என்ற பண்பை கொண்ட கற்பனை அலகு i உடன் கூட்டல் மற்றும் பெருக்கல் செயலிகளின் துணை கொண்டு x + iy என்ற கலப்பெண்ணை பெறலாம். இதில் '+' என்ற குறியீட்டை வெக்டர்களின் கூட்டலாக கருத வேண்டும். இதனை அறிமுகப்படுதியவர் கார்ல் ப்ரீட்ரிக் காஸ் (1777−1855).

1. செவ்வக வடிவம் (Rectangular form)

வரையறை 2.1 (ஒரு கலப்பெண்ணின் செவ்வக வடிவம்)

ஒரு கலப்பெண்ணின் செவ்வக வடிவம் என்பது x + iy (அல்லது x + yi) ஆகும். இங்கு x மற்றும் y ஆகியவை மெய் எண்களாகும். இதில் x என்பது கலப்பெண்ணின் மெய்ப் பகுதி எனவும் y என்பது கற்பனைப் பகுதி எனவும் அழைக்கப்படுகின்றது.

x = 0 எனில், கலப்பெண்ணானது முழுவதும் கற்பனை எண் ஆகும். y = 0 எனில், கலப்பெண்ணானது முழுவதும் மெய் எண் ஆகும். பூஜ்ஜியம் மட்டும் தான் ஒரே நேரத்தில் மெய் எண்ணாகவும் முழுவதும் கற்பனை எண்ணாகவும் இருக்கும். ஒரு கலப்பெண்ணின் திட்ட செவ்வக வடிவம் x +  iy −ஐ z எனக்குறிப்பது வழக்கம். மேலும் x = Re(z) எனவும் y = Im(z) எனவும் குறிக்கலாம். உதாரணமாக, Re(5 − i7) = 5 மற்றும் Im (5 − i7) = −7 ஆகும்.

α + iβ, β ≠ 0 என்ற வடிவில் உள்ள எண்களை கற்பனை எண்கள் (மெய்யற்ற கலப்பெண்கள்) என்கிறோம்.

இரு கலப்பெண்கள் எந்த நிலையில் சமம் எனலாம் என்பதை பின்வருமாரு வரையறுக்கிறோம். 

வரையறை 2.2

இரண்டு கலப்பெண்கள் z1 = x1 + iy1 மற்றும் z2 = x2 + iy2 ஆகியவை சமமாக இருக்கத் தேவையானதும் போதுமானதுமான நிபந்தனை Re(z1) = Re(z2) மற்றும் Im(z1) = Im(z2). அதாவது x1 = x2 மற்றும் y1 =y2.

உதாரணமாக, α + iβ = −7 + 3i எனில், α  = −7 மற்றும் β = 3 ஆகும்.

2. ஆர்கண்ட் தளம் (Argand plane)

ஒரு கலப்பெண் z = x + iy−ஐ ஒரே ஒரு வழியில் (x, y) என்ற மெய் எண்களின் வரிசை ஜோடிகளாக எழுதலாம். 3 − 8i, 6 மற்றும் −4i ஆகிய கலப்பெண்களை முறையே (3,–8), (6, 0), மற்றும் (0,−4) என வரிசை ஜோடிகளாக எழுதலாம். இவ்வாறாக z = x + iy என்ற கலப்பெண்ணை (x, y) என்ற புள்ளியால் ஆய அச்சுத் தளத்தில் தொடர்புபடுத்தலாம். நாம் x அச்சை மெய் அச்சாகவும், y அச்சை கற்பனை அச்சாகவும் கொண்டால் xy −தளத்தை கலப்பெண் தளம் அல்லது ஆர்கண்ட் தளம் என்கிறோம். ஆர்கண்ட் தளம் என்ற பெயரானது சுசர்லாந்தைச் சேர்ந்த கணிதவியலாளர் ஜென் ஆர்கன்ட் (1768– 1822) என்பவரின் நினைவாக பெயரிடப்பட்டுள்ளது.

ஒரு கலப்பெண்ணானது ஒரு புள்ளியை மட்டுமே குறிப்பது இல்லை, மேலும் ஆதியிலிருந்து அப்புள்ளியை குறிக்கும் நிலை வெக்டராகவும் இதனைப் பார்க்கலாம். அந்த எண், அந்த புள்ளி, மற்றும் அந்த வெக்டர் ஆகியவற்றை அணைத்தையும் z என்ற ஒரே எழுத்தால் குறிக்கலாம். வழக்கமாக இணையான நகர்த்தல் மூலம் வெக்டர்களை எவ்வாறு கையாளுவோமோ அதே போல் இங்கும்   செய்யலாம். இப்பாடப்பகுதியில், ℂ என்பது கலப்பெண்களின் கணத்தைக் குறிக்கின்றது. வரைபடம் வாயிலாக ஒரு கலப்பெண்ணினை ℝ2 −ல் ஒரு புள்ளியாகவோ அல்லது ஒரு வெக்டராகவோ ஆர்கண்ட் தளத்தில் பார்க்கலாம்.

விளக்க எடுத்துக்காட்டு 2.1

2 + i, −1 + 2i, 3 − 2i, 0 − 2í, 3 + √−2, −2 − 3i, cos π/6 + isin π/6, மற்றும் 3 + 0i ஆகியவை ஆர்கண்ட் தளத்தில் குறிக்கப்பட்டுள்ளன.

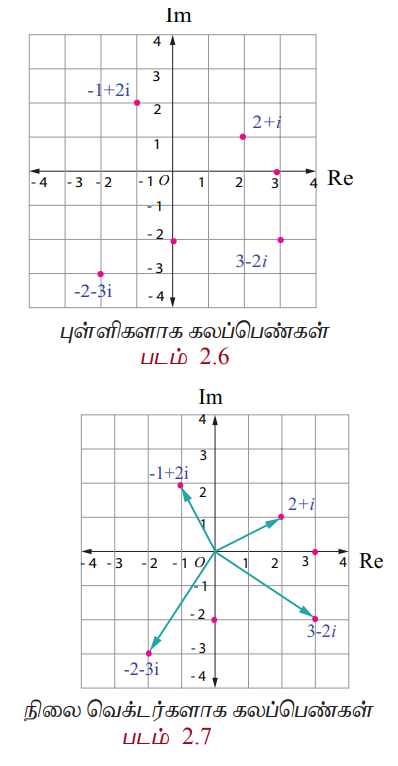
3. கலப்பெண்களின் மீதான இயற்கணிதச் செயல்பாடுகள் (Algebraic operations on complex numbers)

இப்பாடப் பகுதியில், மெய் எண்களின் மீதான பண்புகளை கொண்டு கலப்பெண்களின் இயற்கணித பண்புகளையும் அவற்றின் வடிவியல் அமைப்புகளையும் காண்போம்.

(i) கலப்பெண்ணின் திசையிலிப் பெருக்கம்

z = x + iy மற்றும் k ∈ ℝ, எனில்

kz = (kx) + (ky)i என வரையறுப்போம்.

குறிப்பாக 0z = 0, 1z = z மற்றும் (−1)z = −z ஆகும்.

kz −ன் வரைபடங்கள் k = 2, 1/2, −1 ஆகியவற்றிற்கு கீழே தரப்பட்டுள்ளன.

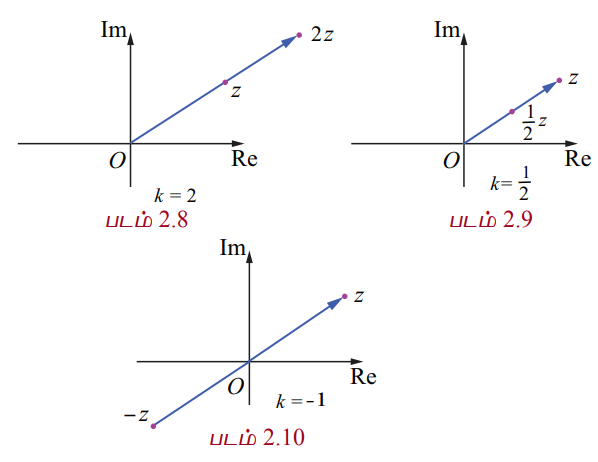
(ii) கலப்பெண்களின் கூட்டல்

z1 = x1 + iy1 மற்றும் z2 = x2 + iy2, இங்கு x1, x2, y1, மற்றும் y2 ∈ ℝ எனில்,

z1 + z2 = (x1 + iy1) + (x2 + iy2)

= (x1 + x2 ) + i (y1 + y2)

z1 + z2 = (x1 + x2) + i (y1 + y2)

என வரையறுப்போம். ஏற்கனவே நாம் ஒரு வெக்டரை இணையாக நகர்த்துவதால் அதன் எண் மதிப்பும் திசையும் மாறாது எனக் கண்டுள்ளோம். z1 = x1 + iy1 மற்றும் z2 = x2 + iy2 எனும் போது வெக்டர் கூட்டலின் இணைகரவிதிப்படி அதன் கூடுதல் z1 + z2 = (x1 + x2) + i(y1 + y2) ஆனது (x1 + x2, y1 + y2) என்ற புள்ளியுடன் தொடர்புபடுத்தப்படுகின்றது. இப்புள்ளியை ஆயத்தொலைகளாகக் கொண்ட வெக்டராகவும் இதனைப் பார்க்கலாம். ஆகவே, z1, z2, மற்றும் z1 + z2 ஆகியவற்றை வரைபடம் வாயிலாக கலப்பெண் தளத்தில் படம் 2.11−ல் உள்ளவாறு காணலாம்.

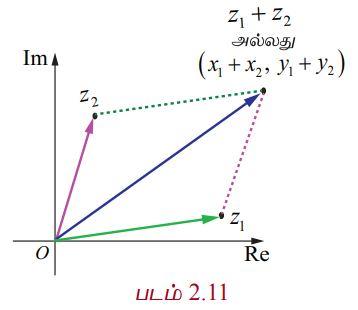
(iii) கலப்பெண்களின் கழித்தல்

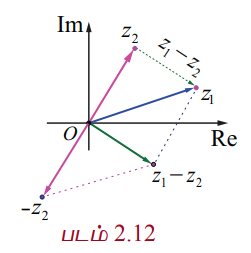
இதுபோலவே z1, −z2, என்ற கலப்பெண்ணை ஆதிப்புள்ளியை ஆரம்பப்புள்ளியாகவும் (x1 – x2, y1 – y2) யை இறுதிப்புள்ளியாகவும் கொண்ட வெக்டராக இதனைப் பார்க்கலாம். 

z1 − z2 = (x1 + iy1) − (x2 + iy2)

= (x1 − x2 ) + i (y1 − y2)

z1 − z2 = (x1 − x2) + i (y1 − y2)

மிக முக்கியமானது என்னவென்றால் z1 − z2 என்ற வெக்டரை z2 −ஐ ஆரம்பப் புள்ளியாகவும் z1 −ஐ முடிவுப் புள்ளியாகவும் கொண்ட வெக்டராகவும் இதனைப் பார்க்கலாம் என்பதாகும். இந்த வகையான குறிப்பிடுதலானது எந்த வகையிலும் கழித்தலின் கருத்துருவை மாற்றுவதில்லை. z1 மற்றும் z2 −ஐ இணைக்கும் கழித்தல் வெக்டரானது புள்ளிக்கோடுகளால் (பச்சை) காட்டப்பட்டுள்ளது.

(iv) கலப்பெண்களின் பெருக்கல்

z1 மற்றும் z2 என்ற கலப்பெண்களின் பெருக்கல் ஆனது 

z1z2 = (x1 + iy1)  (x2 + iy2)

= (x1x2 – y1y2) + i(x1y2 + x2y1)

z1z2 = (x1x2 – y1y2) + i(x1y2 + x2y1) என வரையறுக்கப்படுகின்றது.

z1 மற்றும் z2 −ஐப் பெருக்குவதால் கிடைக்கும் கலப்பெண்ணும் ஒரு வெக்டரை குறிப்பதோடு மட்டுமல்லாமல் அவ்வெக்டரானது z1 மற்றும் z1 ஆகிய வெக்டர்கள் அமைந்த தளத்திலேயே அமையும் இதிலிருந்து இந்த கலப்பெண்களின் பெருக்கம் வெக்டர் இயற்கணிதத்தில் உள்ள வெக்டர்களின் திசையிலி பெருக்கத்தையோ அல்லது வெக்டர்களின் வெக்டர் பெருக்கத்தையோ குறிப்பிடுவது அல்ல என அறியலாம்.

மேற்குறிப்பு

கலப்பெண் z ஐ i ஆல் பெருக்குதல்.

z = x + iy, என்க.

iz = i(x + iy)

= −y + ix.

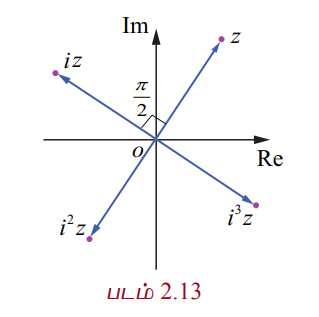
கலப்பெண் iz என்பது கலப்பெண் z −ஐ 90° அல்லது π/2 ரேடியன் கடிகார எதிர்திசையில் ஆதியை பொருத்து சுழற்றுவது ஆகும். பொதுவாக, எந்த கலப்பெண் z −ஐயும் தொடர்ச்சியாக iஆல் பெருக்குவதால் தொடர்ச்சியாக 90° கடிகார எதிர்திசையில் ஆதியை பொருத்து சுழற்றப்படும்.

விளக்க எடுத்துக்காட்டு 2.2

z1 = 6 + 7i மற்றும் z2 = 3 − 5i எனில் z1 + z2 மற்றும் z1 – z2 ஆகியவை 

(i) (3 − 5i) + (6 + 7i) = (3 + 6) + (−5 + 7)i = 9 + 2i

(6 + 7i) − (3 − 5i) = (6 − 3) + (7−(−5))i = 3 + 12i.

z1 = 2 + 3i மற்றும் z2  = 4 + 7i எனில் z1z2 ஆனது

(ii) (2 + 3i)(4 + 7i) = 2 × 4 + 2 × 7i + 4 × 3i + 3 × 7i2

= 8 + 14i + 12i + 21× (−1)

= (8 − 21) + (14 + 12)i = −13 + 26i.

எடுத்துக்காட்டு 2.2

(2 + i)x + (1 − i)y + 2i − 3 மற்றும் x + (−1 + 2i)y + 1 + i ஆகிய கலப்பெண்கள் சமம் எனில் x மற்றும் y−ன் மெய்மதிப்புகளைக் காண்க.

தீர்வு

z1 = (2 + i)x + (1−i)y + 2i − 3 = (2x + y − 3) + i(x− y + 2) மற்றும்

z2 = x + (−1 + 2i)y + l + i = (x – y + 1) + i(2y + 1) என்க.

z1 = z2 எனக் கொடுக்கப்பட்டுள்ளது.

எனவே, (2x + y −3) + i(x – y + 2) = (x – y + 1) + i(2y + 1).

மெய் மற்றும் கற்பனைப் பகுதிகளைச் சமப்படுத்த

2x + y − 3 = x – y + 1 ⇒ x + 2y = 4

x – y + 2 = 2y +  1        ⇒  x − 3y = −1

மேற்கண்ட சமன்பாடுகளைத் தீர்க்க

x = 2 மற்றும் y =1எனப்பெறலாம்.