வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் - டி மாய்வரின் தேற்றம் (de Moivre's Theorem) | 12th Maths : UNIT 2 : Complex Numbers
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 2 : கலப்பு எண்கள்
டி மாய்வரின் தேற்றம் (de Moivre's Theorem)
1. டி மாய்வரின் தேற்றம் (de Moivre's Theorem)
டி மாய்வரின் தேற்றம்
கொடுக்கப்பட்ட கலப்பெண் cos θ + isin θ மற்றும் n என்ற முழு எண்ணிற்கு (cos θ + isin θ)n = (cos nθ + isin nθ)
கிளைத்தேற்றம்
(1) (cos θ − isin θ)n = cos nθ − isin nθ
(2) (cos θ + isin θ)−n = (cos nθ − isin nθ)
(3) (cos θ − isin θ)−n = cos nθ + isin nθ
(4) sin θ + i cos θ = i (cos θ − isin θ).
நாம் இப்பொழுது டிமாய்வரின் தேற்றத்தை கலப்பெண்களை சுருக்குதல் மற்றும் சமன்பாடுகளைத் தீர்த்தல் போன்றவற்றிற்கு பயன்படுத்துவோம்.
எடுத்துக்காட்டு 2.28
z = (cos θ + isin θ) எனில், zn + 1/zn = 2 cos nθ மற்றும் zn − 1/zn = 2isin nθ என நிறுவுக.
தீர்வு
z = (cos θ + isin θ) என்க
டி மாய்வரின் தேற்றப்படி
zn = (cos θ + isin θ)n = (cos nθ + isin nθ)
1/zn = z−n = cos nθ − isin nθ
ஆகவே, zn + 1/zn = (cos nθ + isin nθ) + (cos nθ − isin nθ)
zn + 1/zn = 2 cos nθ
இதுபோலவே,
zn − 1/zn = (cos nθ + isin nθ) − (cos nθ − isin nθ)
zn − 1/zn = 2 isin nθ
எடுத்துக்காட்டு 2.29
சுருக்குக 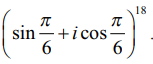
தீர்வு
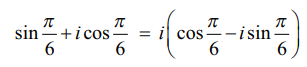 ஆக எழுதலாம்.
ஆக எழுதலாம்.
இருபுறமும் 18−ன் அடுக்கிற்கு உயர்த்த,
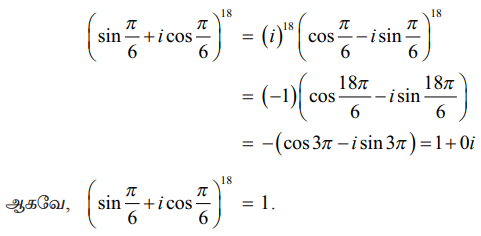
எடுத்துக்காட்டு 2.30
சுருக்குக 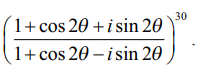
தீர்வு
z = cos 2θ + isin 2θ என்க
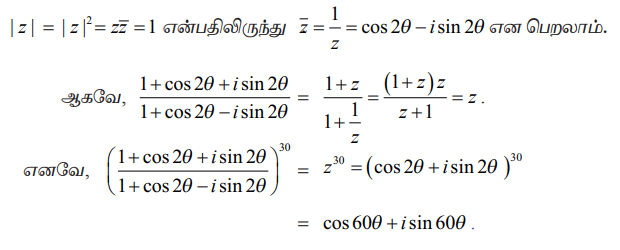
= cos 60θ + isin 60θ .
எடுத்துக்காட்டு 2.31
சுருக்குக (i) (1 + i)l8
(ii) (−√3 + 3i)31
தீர்வு
(i) (1 + i)l8
1 + i = r (cos θ + isin θ) என்க
r = √[12 + 12 ] = √2 ; α = tan−1[1/1] = π/4 ,
θ = α = π/4 (∵ 1 + i ஆனது முதலாம் கால் பகுதியில் உள்ளதால்)
ஆகவே, 1 + i = √2 ( cos π/4 + isin π/4 )
இருபுறமும் 18−ன் அடுக்கிற்கு உயர்த்த,
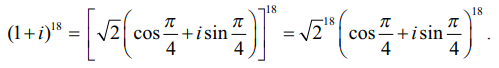
டி மாய்வரின் தேற்றப்படி,
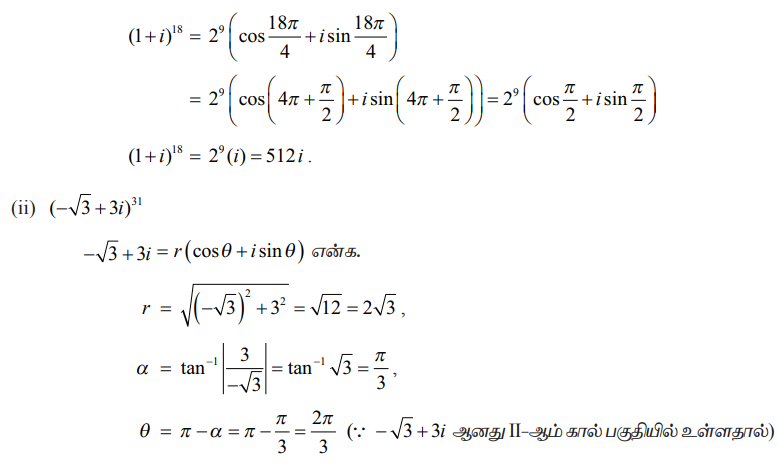
θ = π – α = π – π/3 = 2π/3 (∵−√3 + 3i ஆனது II−ஆம் கால் பகுதியில் உள்ளதால்)
ஆகவே, −√3 + 3i = 2√3 (cos 2π/3 + isin 2π/3)
இருபுறமும் 31−ன் அடுக்கிற்கு உயர்த்த,