வகையீடுகள் (Differentials)

வகையீடுகள் (Differentials)

இங்கு "வகையீடுகள்" பற்றி அறிமுகப்படுத்த மீண்டும் நாம் வகைக்கெழு கருத்துருவைப் பயன்படுத்துவோம். இங்கு சமன்பாடு (1) ஐ கவனிப்போம்.

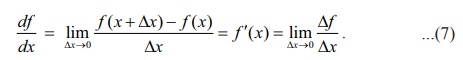
இங்கு df/dx என்பது வித்தியாசங்களின் விகிதத்தின் எல்லை மதிப்பைக் குறிக்க லிபினிட்ஸ் பயன்படுத்திய குறியீடு ஆகும். இது x-ஐப் பொருத்து y-ன் வகைக்கெழு எனப்படும். df/dx -ஐ df மற்றும் dx இவற்றின் விகிதமாக (வகுத்தலாக) கருதுவது பொருத்தமுள்ளதாகுமா? வேறுவிதமாக வகைக்கெழு என்பது df மற்றும் dx -ன் வகுத்தலாகுமாறு df -க்கும் dx -க்கும் பொருள் கொள்ள முடியுமா? சில நேரங்களில் ஆம் எனலாம். எடுத்துக்காட்டாக, f (x) = mx + c இங்கு m, C என்பன மாறிலிகள், எனில் y = f (x).

எல்லா x ∈ R மற்றும் ∆x -க்கு ∆y = f (x + ∆x) - f (x) = m∆x = f'(x)∆x. எனவே சமன்பாடு (2) மற்றும் (3) மெய். இங்கு x மற்றும் y(= f) இவற்றில் ஏற்படும் மாற்றம் நேர்கோட்டின் மீது ஏற்படுகின்றது. இந்நிலையில்

f-ன் மாற்றம் / x-ன் மாற்றம் = ∆y/∆x = f’(x) = df/dx = dy/dx.

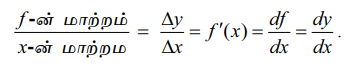
இதனால் df = ∆f = dy மற்றும் dx = ∆x என எடுத்துக்கொண்டால் வகைக்கெழு df/dx என்பதுஉண்மையில் df மற்றும் dx -ன் விகிதமாகும். எனவே f -ன் வகையீட்டை பின்வருமாறு வரையறுப்போம்:

வரையறை 8.4

x -ன் அதிகரிப்பு ∆x உடன் மற்றும் எல்லா x ∈ (a,b) -க்கும் f : (a,b) → R ஒரு வகையிடத்தக்க சார்பு என்க. f -ன் வகையீடு 

df = f'(x) ∆x .... (8)

என வரையறுக்கப்படுகின்றது.

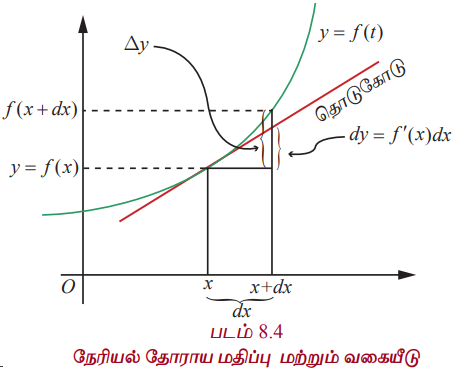
f(x) = x எனில் சமன்பாடு (8)-ன் படி dx = f'(x) ∆x = 1∆x அதாவது dx = ∆x, இது x -அச்சில் ஏற்படும் மாற்றம். எனவே சமன்பாடு (8)-ன்படி f-ன் வகையீடு df = f (x)dx. அடுத்து ஏதேனும் ஒரு y = f (x) – க்கான வகையீட்டை காண்போம். ∆f = f (x+ dx) - f (x) என்பது y = f (x) என்ற சார்பின் வெளியீட்டில் ஏற்படும் மாற்றத்தைத் தருகின்றது. f'(x) என்பது (x, f (x)) என்ற புள்ளியில் தொடுகோட்டின் சாய்வைத் தருகின்றது. தொடுகோட்டுத் திசையில் f இல் ஏற்படும் மாற்றம் dy அல்லது df என்க. எனவே மேற்கண்டபடி dy = f'(x)dx படம் 8.4 இலிருந்து ∆f ≈ dy = df = f'(x)dx என்பது தெளிவு மற்றும் f’(x) என்பது தோராயமாக ∆f மற்றும் ∆x-ன் விகிதமாகக் காணலாம். எனவே df/dx என்பதை df  மற்றும் dx –ன் விகிதமாக பொருள் கொள்ளலாம்.

குறிப்புரை

ஒரு சார்பின் வகைக்கெழுவும் ஒரு சார்புதான் என்பது நாம் அறிவோம். ஒரு சார்பு f-ன் வகையீடு சாரா மாறியின் சார்பாக மட்டுமல்லாமல், உள்ளீட்டில் ஏற்படும் மாற்றம் dx = ∆x -ஐயும் சார்ந்துள்ளது. எனவே, df என்பது x மற்றும் dx என்ற இரு மாறும் அளவுகளின் சார்பாக உள்ளது. ∆f ≈ df என்பதை படம் 8.4-இலிருந்து காணலாம்.

ஒப்பிட்டுப் பார்க்க சில சார்புகள், அவற்றின் வகைக்கெழுக்கள் மற்றும் வகையீடுகள் கீழே உள்ள அட்டவணையில் கொடுக்கப்பட்டுள்ளன.

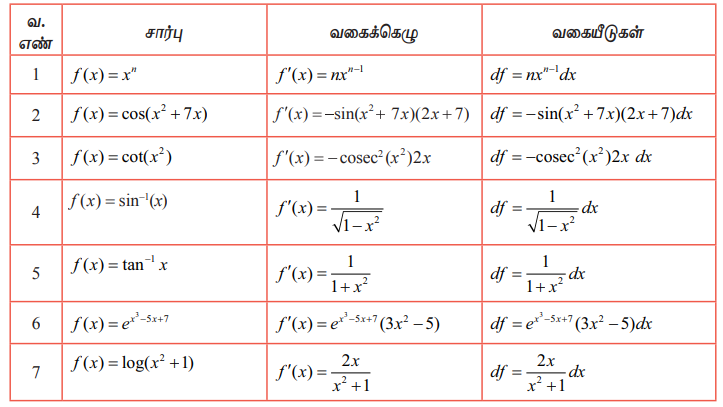
அடுத்து நாம் வகையீடுகளின் பண்புகளைப் பற்றிக் காண்போம். இந்த முடிவுகள் வகைக்கெழுவின் வரையறை மற்றும் வகைக்கெழுவின் விதிகளைப் பின்பற்றி கிடைப்பன. (5)-ம் பண்பிற்கு மட்டும் கீழே நிரூபணம் தரப்பட்டுள்ளது. மற்றவை பயிற்சிக்காக விடப்பட்டுள்ளது.

வகையீடுகளின் பண்புகள் (Properties of Differentials)

இங்கு நாம் மெய்மாறிகளாலான மெய்மதிப்புச் சார்புகளை மட்டும் கருத்தில் கொள்வோம். 

(1) f ஒரு மாறிலிச் சார்பு எனில் df = 0.

(2) சமனிச் சார்பு f (x) = x எனில் df = 1dx. 

(3) f வகையிடத்தக்கது மற்றும், C ∈R எனில் d(cf) = cf'(x)dx .

(4) f g என்பன வகையிடத்தக்கன எனில் d ( f  + g) = df + dg = f (x)dx + g' (x)dx.

(5) f g என்பன வகையிடத்தக்கன எனில் d(fg) = fdg + gdf = ( f (x)g'(x) + f(x)g (x))dx:

(6) f,g என்பன வகையிடத்தக்கன எனில்

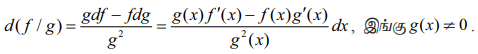
(7) f, g என்பன வகையிடத்தக்கன என்பதுடன் h = f o g வரையறுக்கப்பட்டது எனில்dh = f'(g(x))g'(x)dx . 

(8) h(x) = ef(x) எனில் dh = ef(x) f'(x)dx. 

(9) எல்லா x-க்கும் f (x) > 0 மற்றும் g(x) = log( f (x)) எனில் dg = f’(x) / f(x) dx.

எடுத்துக்காட்டு 8.5

f,g:(a,b) → ℝ என்பன வகையிடத்தக்க சார்புகள் எனில் d(fg) = fdg + gdf என நிறுவுக. 

தீர்வு

f,g : (a,b) → ℝ என்பன வகையிடத்தக்க சார்புகள் என்பதுடன் h(x) = f (x)g(x) என்க. h என்பது வகையிடத்தக்க சார்புகளின் பெருக்கல் என்பதால் (a, b) இல் h-ம் வகையிடத்தக்கது. எனவே வரையறைப்படி dh = 'h'(x)dx.

தற்போது பெருக்கல் விதியைப் பயன்படுத்தி h'(x) = f(x)g'(x) + f'(x)g(x) . இதனால் dh = h' (x)dx = (f (x)g'(x) + f (x)g(x))dx = f (x)g'(x)dx + f '(x)g(x)dx 

= f (x)dg + g(x)df = fdg + gdf 

எடுத்துக்காட்டு 8.6

g(x) = x2 + sinx எனில் dg -ஐக் காண்க. 

தீர்வு

சார்பு g வகையிடத்தக்கது என்பதைக் கவனிக்கவும். மேலும் g'(x) = 2x + cos x இதனால் dg = (2x + cos x)dx . 

எடுத்துக்காட்டு 8.7

10 செமீ ஆரம் உள்ள கோளத்தின் ஆரம் 0.1 செமீ குறைகின்றது எனில் அதன் கன அளவில் தோராயமாக எவ்வளவு குறையும்? 

தீர்வு

கோளத்தின் கன அளவு V = 4/3 πr3 என நாம் அறிவோம். இங்கு r > 0 என்பது ஆரம். எனவே வகையீடு dV = 4πr2 dr மற்றும்∆V  ≈ dV எனவே

dV = 4 π(10)2 (9.9 -10)cm3

= 4π102 (-0.1)cm3 

= - 40π cm3

ஆரம் 10-இலிருந்து 9.9 ஆக குறைகின்றதால் dr = (9.9 - 10) செமீ எனப் பயன்படுத்தியுள்ளோம். மறுபடியும் விடையில் வரும் - குறியீடு கோளத்தின் கன அளவு 40π செமீ3 குறைவதைக் குறிக்கின்றது.