விளிம்பு விளைவு

விளிம்பு விளைவு (Diffraction)

ஒலி அலை, ஒளி அலை, நீரலை போன்ற அனைத்து அலைகளுக்குமான பொதுவான பண்பு விளிம்பு விளைவாகும். தடையின் விளிம்பில் வளைந்து சென்று, தடையின் வடிவியல் ரீதியான நிழலுக்குள் அலை செல்லும் நிகழ்வுக்கு விளிம்பு விளைவு என்று பெயர். கதிர் ஒளியியலில் நாம் பயின்ற ஒளியின் நேர்கோட்டுப்பரவலுக்கு இது எதிரானதாகும். ஏனெனில், ஊடகம் ஒன்றின் வழியே செல்லும் ஒளிக்கற்றை எவ்வித வளைவும் இன்றி நேர்கோட்டுப் பாதையில் செல்லும். ஆனால், தடையின் அளவு ஒளியின் அலைநீளத்துடன் ஒப்பிடத்தக்க அளவில் காணப்பட்டால் மட்டுமே விளிம்பு விளைவு ஏற்படும். இதன் காரணமாகத்தான். கதவுகள், ஜன்னல்கள் மற்றும் கட்டடங்களினால் ஒலி அலைகள் விளிம்பு விளைவு அடைகின்றன. ஒலியின் அலைநீளம் இத்தடைகளின் அளவுடன் ஒப்பிடத்தக்க அளவில் உள்ளதால் விளிம்பு விளைவு ஏற்படுகின்றது. ஒளியிலும் விளிம்பு விளைவு ஏற்பட, தடையின் அளவு ஒளியின் அலைநீளத்துடன் ஒப்பிடத்தக்க அளவில் இருக்க வேண்டும்.

1. ப்ரனெல் மற்றும் ப்ரானோஃபர் (Fresnel and Fraunhofer) விளிம்பு விளைவுகள்

விளிம்பு விளைவடையும் அலைமுகப்பின் வடிவத்தைப் பொருத்து ப்ரனெல் மற்றும் ப்ரானோஃபர் விளிம்பு விளைவு என இருவகைப்படுத்தலாம். ப்ரெனல் மற்றும் ப்ரானோஃபர் விளிம்பு விளைவுகளுக்கிடையேயான வேறுபாடுகள் அட்டவணை 6.4 இல் காட்டப்பட்டுள்ளது

உற்று நோக்கல் மற்றும் ஆய்வு செய்ய ப்ரானோஃபர் விளிம்பு விளைவு எளியதாக இருப்பதால் ப்ரானோஃபர் விளிம்பு விளைவுப் பற்றி நாம் மேலும் படிக்கலாம்.

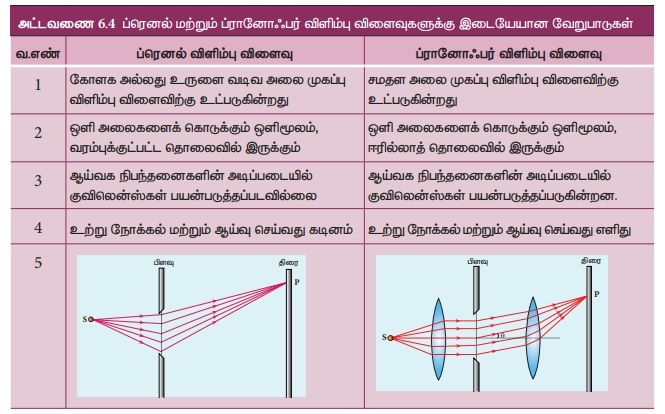
2. ஒற்றைப் பிளவில் ஏற்படும் விளிம்பு விளைவு (Diffraction at single slit)

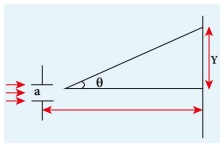
AB அகலம் கொண்ட ஒற்றைப் பிளவு ஒன்றின் மீது செங்குத்தாக விழும் இணை ஒளிக்கற்றையைக் கருதுவோம். இது படம் 6.63 இல் காட்டப்பட்டுள்ளது. விளிம்பு விளைவடைந்த ஒளிக்கற்றை, தொலைவில் வைக்கப்பட்டுள்ள திரையில் விழுகிறது பிளவின் மையத்தை O என்க. பிளவின் தளத்திற்குச் செங்குத்தாக C புள்ளி வழியே செல்லும் நேர்கோடு திரையில் 0 என்ற புள்ளியை அடைகிறது. திரையில் ஏதேனும் ஒரு புள்ளியின் அதாவது P புள்ளியின் ஒளிச்செறிவைக் நாம் கண்டுபிடிக்கலாம். பிளவின் வெவ்வேறு புள்ளிகளில் இருந்து P ஐ அடையும் நேர்கோடுகளை நாம் செங்குத்துக் கோடோடு θ கோணத்தை ஏற்படுத்தும் இணை கோடுகளாகக் கருதலாம்.

பிளவின் வெவ்வேறு புள்ளிகளிலிருந்து வரும் இணை ஒளி அலைகள் திரையில் P புள்ளி மற்றும் இதர புள்ளிகளில் ஒன்றை ஒன்று குறுக்கிட்டுத் தொகுபயன் ஒளிச்செறிவைக் கொடுக்கின்றன. P புள்ளி, வடிவியல் ரீதியான நிழல் பகுதியில் உள்ளது. விளிம்பு விளைவின் காரணமாக, இப்பகுதி வரை மையப்பெருமம் பரவி காணப்படுகிறது. இது படம் 6.63 இல் காட்டப்பட்டுள்ளது. திரையில் உள்ள புள்ளி P வெவ்வேறு சிறுமங்களை அடைவதற்கான நிபந்தனைகளைக் நாம் காணவேண்டும். பிளவை இரட்டைப்படை எண்ணிக்கையுடைய சிறுசிறு பகுதிகளாகப் பிரித்துக் கொண்டால் அப்பகுதிகளிலிருந்து வரும் ஒளி அலைகளின் பாதை வேறுபாடுகள் ஒன்றினைத்து, P புள்ளியில் அழிவுக் குறுக்கீட்டுவிளைவை ஏற்படுத்தி, சிறும ஒளிச்செறிவை உண்டாக்குகிறது. பெருமங்களை விளக்குவதற்கு, பிளவை ஒற்றைப்படை எண்ணிக்கையுடைய சிறு பகுதிகளாகப் பார்த்துக்கொள்ள வேண்டும்.

P புள்ளியில் முதல் சிறுமம் ஏற்படுவதற்கான நிபந்தனை

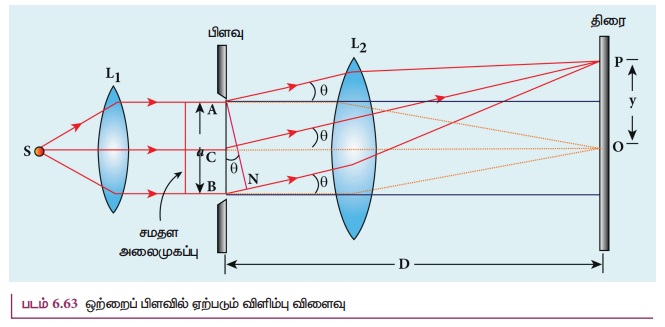
பிளவு AB ஐ AC மற்றும் CB என்ற இரண்டு அரைப்பகுதிகளாக பிரித்துக் கொள்ள வேண்டும். தற்போது AC யின் அகலம் (a/2) ஆகும். பிளவில் (a/2) அகலமுடைய வெவ்வேறு புள்ளிகளுக்கு ஒத்த புள்ளிகள் (Corresponding points) என்று பெயர். இது படம் 6.64 இல் காட்டப்பட்டுள்ளது.

வெவ்வேறு ஒத்த புள்ளிகளிலிருந்து வரும் ஒளி அலைகள் P புள்ளியில் ஒன்றுடன் ஒன்று மேற்பொருந்தி அழிவுக் குறுக்கீட்டு விளைவை ஏற்படுத்தி, முதல் சிறுமத்தை ஏற்படுத்துகிறது. ஒத்த புள்ளிகளிலிருந்து வரும் ஒளி அலைகளின் பாதை

வேறுபாடு, δ = a/2 sinθ

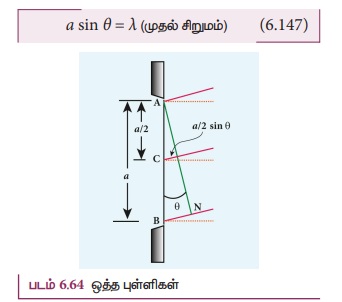
P புள்ளியின் முதல் சிறுமம் தோன்றுவதற்கான

நிபந்தனை, a/2 sinθ = λ/2

P புள்ளியில் இரண்டாவது சிறுமம் தோன்றுவதற்கான நிபந்தனை

AB பிளவை a/4 அகலம் கொண்ட நான்கு பகுதிகளாகப் பிரித்துக் கொள்ள வேண்டும். பிளவின் நடுவே a/4 அகலம் கொண்ட ஒத்த புள்ளிகளிலிருந்து வரும் ஒளி அலைகளுக்கு இடையேயான பாதை

வேறுபாடு, δ = a/4 sinθ

P புள்ளியில் இரண்டாம் சிறுமம தோன்றுவதற்கான நிபந்தனை,a/4 sinθ = λ/2

a sinθ = 2λ (இரண்டாவது சிறுமம்) (6.148)

P புள்ளியில் இரண்டாம் சிறுமம் தோன்றுவதற்கான நிபந்தனை

முன்னர் கூறியவாறே, பிளவை ஆறு சம பிரிவுகளாகப் பிரித்துக்கொள்ள வேண்டும். P புள்ளியில் மூன்றாவது சிறுமம் ஏற்படுவதற்கான 

நிபந்தனை, a/6 sin θ = λ/2

P புள்ளியில் n வது சிறுமம் ஏற்பட நிபந்தனை

பிளவை, 2n எண்ணிக்கையுடைய (இரண்டை இலக்க எண்ணிக்கை) சமபகுதிகளாகப் பிரித்துக்கொள்ள வேண்டும். ஓர் ஒத்த புள்ளியிலிருந்து வரும் ஒளி அலையை மற்றோர் ஒத்த புள்ளியிலிருந்து வரும் ஒளி அலை அழிக்கும் நிலையில் n வது சிறுமம் ஏற்பட நிபந்தனை,

a/2n sinθ = λ/2

பெருமங்களுக்கான நிபந்தனை

பெருமஒளிச்செறிவு ஏற்பட , பிளவை ஒற்றைப்படை எண்ணிக்கையுடைய

சம்பகுதிகளாகப் பிரித்துக்கொள்ள வேண்டும். இவ்வாறு பிரிப்பதனால் ஏதாவது ஒரு ஒத்த புள்ளியிலிருந்து வரும் ஒளி அலை அழிக்கப்படாமல் இருக்கும். எனவே, P புள்ளி பெரும ஒளிச்செறிவில் காணப்படும்.

முதல் பெருமத்திற்கான நிபந்தனை,

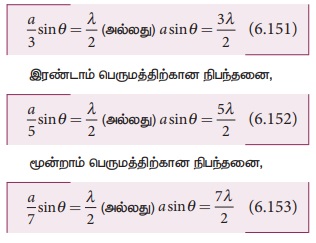
இதேபோன்று, n வது பெருமத்திற்கான நிபந்தனை

இங்கு n = 0,1,2,3...... என்பது பெருமங்களின் வரிசையாகும்.

மைய வரிசை பெருமத்திற்கு, சுழி வரிசை பெருமம் என்று பெயர். அடுத்தடுத்த சிறுமங்களுக்கு கிட்டத்தட்ட நடுவே பெரும ஒளிச்செறிவு காணப்படும்.

இங்கு sinθ என்பது விளிம்பு விளைவின் கோண பரவலைக் கொடுக்கிறது. தோராயமாக்கலின் அடிப்படையில் திரையின் மையத்திலிருந்து y தொலைவில் அமைந்துள்ள பெருமம் அல்லது சிறுமத்தின் நிலையை sinθ விற்கு பதிலாக tanθ கொண்டும் விவரிக்கலாம். (ஏனெனில் θ

மிகவும் சிறியது) எனவே sinθ = tanθ = y/D

இங்கு, y என்பது திரையின் மையத்திலிருந்து பெருமம் அல்லது சிறுமம் அமைந்துள்ள நிலையைக் குறிக்கிறது. மேலும் D என்பது ஒன்றைப்பிளவிலிருந்து திரை உள்ள தொலைவைக் குறிக்கிறது.

எடுத்துக்காட்டு 6.31

500 nm அலைநீளமுடைய ஒளி அலை, 0.2 mm அகலமுடைய பிளவு ஒன்றின் வழியே செல்லும்போது விளிம்பு விளைவு அடைகிறது. பிளவிலிருந்து 60 cm தொலைவில் விளிம்பு விளைவுப்பட்டை கிடைக்கிறது எனில், பின்வருவனவற்றைக் கணக்கிடுக.

(i) மையப்பொலிவின் கோணப் பரவல்

(ii) மையப்பெருமத்திலிருந்து இரண்டாவது சிறுமம் அமைந்துள்ள தொலைவு.

தீர்வு

λ = 500 nm = 500x10^-9 m; a = 0.2 mm = 0.2x10^-3 m; D = 60 cm = 60x10^-2m

(i) விளிம்பு விளைவு சிறுமத்திற்கான சமன்பாடு, a sin θ = nλ

முதல் சிறுமம் வரை, மையப்பெருமம் பரவியிருக்கும் எனவே , n = 1

சமன்பாட்டினை மாற்றியமைக்கும் போது,

sinθ = λ/a அல்லது θ = sin^-1   (λ/a)

மதிப்புகளைப் பிரதியிடும்போது,

θ =sin^-1 (500x10^-9 /0.2 x 10^-3) = sin_­^-1 (2.5x10^-3)

θ = Sin | 0.2x10)

θ = 0.0025 rad

(ii) முதல் சிறுமம் வரை பரவியிருக்கும் மையப்பெருமத்தின் மதிப்பு, y₁ ஐக்கான (n = 1) என்க. எனவே, a sin θ = λ

θ மிகவும் சிறியது தோராயமாக்கல் நிபந்தனைப்படி,

sinθ ͠ tanθ = y₁/D

a y₁/D = λ  மாற்றியமைக்கும்போது, y₁= λD/a =

மதிப்புகளைப் பிரதியிடும்போது,

y₁ = 500x10^-9 x 60 x 10^-2 / 0.2 x 10^-3 =1.5x10^-3 =1.5 mm

இரண்டாவது சிறுமத்திற்கான y₂ மதிப்பைக்கான (n = 2) என்க. எனவே a sin θ = 2λ

a y₂/D = 2λ மாற்றியமைக்கும்போது, y₂ = 2λD/a மதிப்புகளைப் பிரதியிடும்போது,

y₂ = 2X500 x 10^-9 x 60 x 10^-2 / 0.2x10^-3 = 3x10^-3 = 3 mm

மையப்பெருமத்திற்கும், இரண்டாவது சிறுமத்திற்கும் உள்ள தொலைவு y₂ – y₁

y₂ – y₁ = 3 mm - 1.5 mm = 1.5 mm

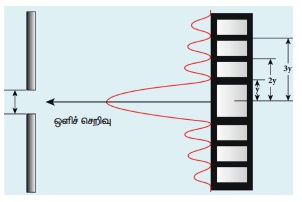
குறிப்பு: ஒற்றைப் பிளவில் ஏற்பட்ட விளிம்பு விளைவில், மையப்பெருமத்தின் தடிமன், மற்ற பெருமங்களைப்போல் இருமடங்கு தடிமனுடையது என்பதை மேற்கண்ட கணக்கீடு காட்டுகிறது. மேலும், பொலிவு மற்றும் கருமை பட்டைகளின் தடிமன் வெவ்வேறானவை.

எடுத்துக்காட்டு 6.32

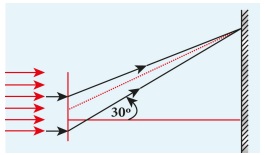
5000 Å அலைநீளமுடைய ஒற்றைநிற ஒளி, ஒற்றைப்பிளவின் வழியே சென்று விளிம்பு  விளைவடைந்து படத்தில் காட்டியுள்ளவாறு மையப்பெருமத்தை ஏற்படுத்துகிறது. விளிம்பு விளைவை ஏற்படுத்தும் பிளவின் தடிமனைக் காண்க.

தீர்வு

λ = 5000 Å = 5000x10^-10 m; sin 30° = 0.5; n = 1; a = ?

விளிம்பு விளைவு சிறுமத்திற்கான சமன்பாடு, asin θ = nλ

மையப்பெருமம், முதல் சிறுமம் வரை பரவிக்காணப்படும் எனவே, n = 1

சமன்பாட்டை மாற்றியமைக்கும்போது , a = λ/sinθ

மதிப்புகளைப் பிரதியிடும் போது , a = 5000x10^-10 / 0.5

a =1x10^-6m = 0.001x10^-3m = 0.001mm

3. முதல் சிறுமத்தைப் பற்றிய விளக்கம்

முதல் சிறுமத்திற்கான நிபந்தனையைக் கருதுக. இங்கு n = 1

a sin θ = λமுதல் சிறுமத்தின் கோண பரவல், sinθ = λ/a

இதற்கான சிறப்பு நேர்வுகள் பின்வருமாறு :

(i) a < λ எனும்போது, விளிம்பு விளைவு சாத்தியமல்ல. ஏனெனில் sinθ எப்போதும் ஒன்றைவிட அதிக மதிப்பைப் பெறாது.

(ii) a ≥ λ, எனும்போது, விளிம்பு விளைவு சாத்தியமாகும்.

*  a = λ எனில் sinθ = 1 அதாவது θ = 90°. இதன் பொருள் முதல் சிறுமம் 90° இல் ஏற்படுகிறது என்பதாகும். எனவே, வடிவியல் ரீதியான நிழல் பகுதி முழுவதும் மையப்பெருமம் பரவி, விளிம்பு விளைவுக் கதிரை 90° வளைக்கிறது.

* a >> λ விற்கு sinθ << 1 அதாவது, முதல் சிறுமம் பிளவின் அகலத்திற்குள்ளாகவே அமையும். எனவே, விளிம்பு விளைவைக்

காண இயலாது.

(iii) a > λமற்றும் அலைநீளத்துடன் ஒப்பிடத்தக்க அளவில் அமையும் போது அதாவது a = 2λ

எனும்போது, sinθ λ/a = λ/2 λ  = ½ .எனவே

θ = 30°. மேற்கண்ட மூன்று நேர்வுகளும் விளிம்பு விளைவினைத் தெளிவாகக் காணும் வழிமுறையாகும்.

4. ப்ரனெல் தொலைவு

ஒளியின் நேர்கோட்டுப் பரவல், கதிர்ஒளியியலில் சாத்தியமாகும் தொலைவிற்கு ப்ரனெல் தொலைவு என்று பெயர். விளிம்பு விளைவு நிகழ்வில் ஒளி அலை வளைந்து செல்லும் இந்த ஒளியின் வளையும் பண்பு அதன் நேர்கோட்டுபரவலுக்கு முற்றிலும் எதிரானதாகும். ஆனால் இந்த விளைவு மையப்பெருமத்தை கடக்கும் வரை எந்த முக்கியத்துவத்தையும் பெறாது. அதாவது படம் 6.65இல் z தொலைவைக் கடக்கும் வரை எந்த முக்கியத்துவத்தையும் பெறாது. எனவே, ப்ரனெல் தொலைவு என்பது எந்த தொலைவு வரை ஒளி, கதிர் ஒளியியலுக்கு கட்டுப்படுகிறதோ அல்லது கதிர் ஒளியியலுக்கு கட்டுப்படாமல் அலை ஒளியியலுக்கு கட்டுப்படத்தொடங்குகிறதோ அந்தத் தொலைவே ப்ரனெல் தொலைவு எனப்படும்.

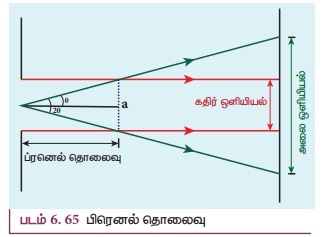
முதல் சிறுமத்திற்கான விளிம்பு விளைவுச் சமன்பாடு sinθ = λ/a ; θ = λ/a

ப்ரனெல் தொலைவின் வரையறையிலிருந்து, sin2θ =a/z; 2θ= a/z

இரண்டு சமன்பாடுகளையும் ஒப்பிடும்போது,

λ/a  = a/2z

எனவே, ப்ரனெல் தொலைவு Z

எடுத்துக்காட்டு 6.33

500 nm அலைநீளமுடைய ஒளி 5 mm அகலமுடைய துளையின் வழியேச் செல்லும்போது விளிம்பு விளைவு அடைகிறது. இந்நிகழ்வில் கதிர் ஒளியியலைப் பயன்படுத்தும் தொலைவினைக் காண்க

தீர்வு

a = 5 mm = 5 x 10^-3 m;

λ = 500 nm = 500x10^-9m; z = ?

ப்ரனெல் தொலைவு, z = a² / 2λ

மதிப்புகளைப் பிரதியிடும்போது,

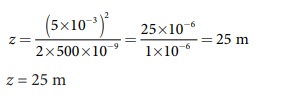
5. குறுக்கீட்டு விளைவிற்கும், விளிம்பு விளைவிற்கும் உள்ள வேறுபாடுகள்

குறுக்கீட்டு விளைவு மற்றும் விளிம்புவிளைவு இரண்டையும் வேறுபடுத்திப்பார்ப்பது மிகவும் கடினமாகும். ஏனெனில், இவ்விரண்டு பண்புகளும் ஒளியின் அலைப்பண்பினால் ஏற்படுவனவாகும். இவ்விரண்டு நிகழ்வுகளிலும் ஒளி வடிவியல் ரீதியான நிழற்பகுதியை அடைந்து ஒன்றுடன் ஒன்று குறுக்கீடு அடைந்து பெருமங்கள் மற்றும் சிறுமங்களைத் தோற்றுவிக்கின்றன. இருந்தபோதிலும், இவ்விரண்டு விளைவுகளின் தோற்றத்தின் அடிப்படையில் பின்வரும் வேறுபாடுகள் கண்டுணரப்பட்டு அட்டவணை 6.5இல் கொடுக்கப்பட்டுள்ளன.

6. கீற்றணியில் ஏற்படும் விளிம்பு விளைவு

விளிம்பு விளைவுக் கீற்றணியில் சம அகலமுடைய , அதிக எண்ணிக்கையில் அமைந்த பிளவுகள் காணப்படுகின்றன. பிளவுகளின் அகலம் விளிம்பு விளைவடையும் ஒளியின் அலைநீளத்துடன் ஒப்பிடத்தக்க அளவில் அமைந்திருக்கும். ஒளிபுகும் பொருளின் மீது வைர ஊசியினைக் கொண்டு ஒளிபுகாக்கோடுகள் வரையப்பட்டிருக்கும். வணிகரீதியில் செயல்படும் நவீன விளிம்பு விளைவுக் கீற்றணியில் ஒரு சென்டிமீட்டரில் 6000 ஒளிபுகாக் கோடுகள் வயைரப்பட்டிருக்கும். தடை போன்று செயல்படும், ஒளிபுகாக் கோடுகளின் அகலத்தை எனவும், ஒளிபுகாக் கோடுகளுக்கு நடுவே அமைந்துள்ள துளை போன்று செயல்படும் ஒளிபுகும் பகுதியின் அகலத்தை a எனவும் கொள்க. ஓர் ஒளிபுகாக் கோடு மற்றும் ஓர் ஒளிபுகும் பிளவு ஆகியவற்றின் மொத்த அகலத்திற்கு கீற்றணிமூலம் (e=a + b) என்று பெயர். அடுத்தடுத்த பிளவுகளில் உள்ள, கீற்றணி மூலத்திற்குச் சமமான தொலைவில் அமைந்துள்ள புள்ளிகளுக்கு ஒத்த புள்ளிகள் என்று பெயர்.

குறுக்கீட்டு விளைவு      

1. இரண்டு ஒளி அலைகள் ஒன்றின் மீது மற்றொன்று 

2. இரண்டு வெவ்வேறு ஓரியல் மூலங்களிலிருந்து  வரும் அலைமுகப்புகள் மேற்பொருந்துகின்றன

3. ஒளிப்பட்டைகளுக்கு இடையே உள்ள தொலைவு சமம்

4. எல்லா பொலிவுப்பட்டைகளும் கிட்டத்தட்டஒரே ஒளிச்செறிவைப் பெற்றிருக்கும்.

5. ஒளிப்பட்டைகளின் எண்ணிக்கை அதிகம்

விளிம்பு விளைவு

1. மேற்பொருந்துகின்றன தடையின் விளிம்பில் ஒளி அலைகள் வளைந்து  செல்கின்றன

2. ஒரே அலைமுகப்பில் உள்ள பல்வேறு புள்ளிகளிலிருந்து வரும் அலைமுகப்புகள் மேற்பொருந்துகின்றன.

3. சமமற்ற இடைவெளிகளில் ஒளிப்பட்டைகள்  தோன்றுகின்றன

4. உயர் வரிசை விளிம்பு விளைவுப்பட்டைகளின் ஒளிச்செறிவு வேகமாய்க் குறையும்.

5. ஒளிப்பட்டைகளின் எண்ணிக்கை குறைவு

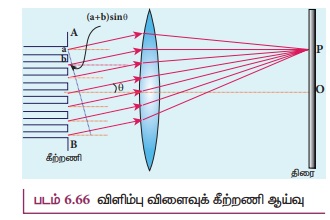
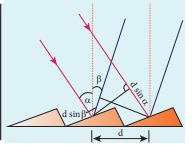
சமதள விளிம்பு விளைவுக் கீற்றணி AB ஐக் கருதுக. இக்கீற்றணியில், சம அகலம் a கொண்ட அடுத்தடுத்த பிளவுகளும், சம அகலம் b கொண்ட ஒளிபுகாக் கோடுகளும் படம் 6.66இல் காட்டியுள்ளவாறு அமைந்துள்ளன. λ அலைநீளமுடைய ஒற்றைநிறச் சமதள அலைமுகப்பு ஒன்று கீற்றணியின் மீது செங்குத்தாக விழுகின்றது எனக் கருதுக. கீற்றணியின் மீது விழும் ஒளியின் அலைநீளம், பிளவின் அகலத்துடன் ஒப்பிடத்தக்க அளவில் உள்ளதால், கீற்றணியால் அவ்வொளி விளிம்பு விளைவு அடையும். குவிலென்ஸ் ஒன்றை பயன்படுத்தி விளிம்புவிளைவடைந்த அலைகளை திரையின் மீது குவித்தால், விளிம்பு விளைவுப்பட்டை அமைப்பு கிடைக்கும். கீற்றணியின் மையத்திலிருந்து திரைக்கு வரையப்பட்ட செங்குத்துக் கோட்டுடன் θ கோணத்தில் அமைந்துள்ள P என்ற புள்ளியைக் கருதுக . ஒரு ஜோடி ஒத்த புள்ளிகளிலிருந்து சென்ற விளிம்பு விளைவடைந்த அலைகளுக்கிடையேயான பாதை வேறுபாடு

அனைத்து ஜோடி ஒத்த புள்ளிகளுக்கும் இப்பாதை வேறுபாடு சமமாகும். P புள்ளி பொலிவுடன் இருக்க,

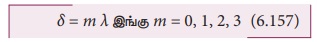
மேற்கண்ட இரண்டு சமன்பாடுகளையும் ஒப்பிடும்போது,

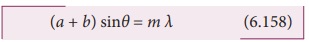
இங்கு m என்பது விளிம்பு விளைவு வரிசையாகும்.

சுழி வரிசைப் பெருமத்திற்கான நிபந்தனை, m = 0

(a + b) sinθ = 0 எனில், விளிம்பு விளைவுக் கோணம் θ = 0. sinθ = 0 மற்றும் m = 0 இதற்கு சுழி வரிசைப் பெருமம் அல்லது மையப்பெருமம் என்று பெயர்.

முதல் வரிசைப் பெருமத்திற்கான நிபந்தனை m = 1

(a + b) sinθ₁ = λ எனில், விளிம்பு விளைவடைந்த ஒளி படும் ஒளியின் திசையுடன் θ₁, கோணத்தை ஏற்படுத்தும். மேலும், முதல் வரிசைப் பெருமம் கிடைக்கும்.

இரண்டாம் வரிசைப் பெருமத்திற்கான நிபந்தனை m = 2

(a + b) sinθ₂ = 2λ எனில், விளிம்பு விளைவடைந்த ஒளி படும் ஒளியின் திசையுடன் θ₂, கோணத்தை ஏற்படுத்தும். மேலும், இரண்டாம் வரிசை பெருமம் கிடைக்கும்.

உயர் வரிசைப் பெருமம் கிடைக்க நிபந்தனை

மையப் பெருமத்தின் இரண்டு பக்கங்களிலும் வெவ்வேறு கோண நிலைகளில் உயர்வரிசைப் பெருமங்கள் கிடைக்கும். இவ்வாறாக எடுத்துக்கொண்டால்,

கீற்றணியில் ஓரலகு அகலத்திற்கு வரையப்பட்ட கீற்றணி மூலங்கள் அல்லது ஒளிபுகாக் கோடுகளின் எண்ணிக்கையை N கொடுக்கும். பொதுவாக, கீற்றணியிலேயே N இன் மதிப்பு எழுதப்பட்டிருக்கும். எனவே,

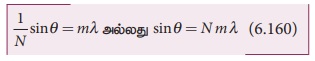
ஒற்றைப்பிளவு ஆய்வில் சிறுமத்திற்கான நிபந்தனை sinθ = n/λ இங்கு n என்பது, சிறுமங்களின் வரியைக் குறிக்கும். ஆனால் விளிம்பு விளைவுக் கீற்றணி ஆய்வில் பெருமத்திற்கான நிபந்தனை sin_g = Nmλ . இங்கு m என்பது பெரும விளிம்பு விளைவு வரிசையைக் குறிக்கும் என்பதை மாணவர்கள் கவனமுடன் நினைவில் வைத்திருக்க வேண்டும்.

எடுத்துக்காட்டு 6.34

ஒரு சென்டிமீட்டரில் 4000 ஒளிபுகும் பிளவுகள் கொண்ட விளிம்பு விளைவுக் கீற்றணி ஒன்று ஒற்றை நிற ஒளியினால் ஒளியூட்டப்படுகிறது. இவ்வமைப்பினால் 30° கோணத்தில் இரண்டாம் வரிசை விளிம்பு விளைவு தோன்றுகிறது எனில், பயன்படுத்தப்படும் ஒற்றை நிற ஒளியின் அலை நீளத்தைக் காண்க.

தீர்வு

1 cm நீளத்திற்கு வரையப்பட்ட கோடுகளின் எண்ணிக்கை 4000; விளிம்பு விளைவு வரிசை m = 2 ;

விளிம்பு விளைவுக்கோணம், θ = 30°;

ஒளியின் அலைநீளம் λ = ?

ஓரலகு நீளத்திற்கு வரையப்பட்ட கோடுகளின் எண்ணிக்கை,

 N = 4000  1 x 10^-2 =  4 x 10⁵

விளிம்பு விளைவுப் பெருமத்திற்கான சமன்பாடு, sinθ = Nmλ

மாற்றி அமைக்கும்போது, λ = sinθ = Nm

மதிப்புகளைப் பிரதியிட்டால்,

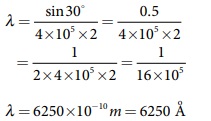
எடுத்துக்காட்டு 6.35

500 nm அலைநீளமுடைய ஒற்றை நிற ஒளியானது விளிம்பு விளைவுக் கீற்றணியின் மீது, விழுகிறது. 30° கோணத்தில் நான்காம் வரிசை பெரும ஒளிச்செறிவு வரி கிடைக்கிறது எனில், கீற்றணியில் ஒரு சென்டிமீட்டர் அகலத்திற்கு அமைந்துள்ள பிளவுகளின் எண்ணிக்கையைக் காண்க.

தீர்வு

ஒளியின் அலைநீளம் λ = 500 nm = 500x10^-9 m;

விளிம்பு விளைவு வரிசை; m = 4;

விளிம்பு விளைவுக் கோணம் θ = 30°;

ஒரு சென்டிமீட்டர் அகலத்தில் அமைந்துள்ள பிளவுகளின் எண்ணிக்கை = ? விளிம்பு விளைவுப் பெருமத்திற்கான சமன்பாடு, sin θ = Nmλ

மாற்றியமைக்கும்போது , N = sinθ /mλ

மதிப்புகளைப் பிரதியிடும்போது,

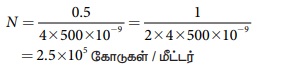
ஒரு சென்டிமீட்டரில் அமைந்துள்ள கோடுகளின் எண்ணிக்கை

2.5 x 10⁵ x10^-2 = 2500 கோடுகள் / மீட்டர்

7. ஒற்றைநிற ஒளியின் அலைநீளத்தைக் காண்பதற்கான சோதனை

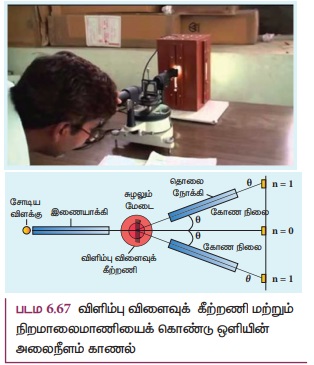
விளிம்பு விளைவுக் கீற்றணி மற்றும் நிறமாலைமாணியைக் கொண்டு நிறமாலைவரியின் அலைநீளத்தைத் துல்லியமாகக் கண்டறியலாம். நிறமாலைமானியின் தொடக்க சீரமைப்புகளை சரிசெய்ய வேண்டும். அலைநீளம் காணவேண்டிய ஒற்றை நிற ஒளியினால் இணையாக்கியின் பிளவினை ஒளியூட்டவேண்டும். தொலைநோக்கியினை இணையாக்கிக்கு நேராக அமைத்துப் பிளவின் நேரடி பிம்பத்தினைக் காணவேண்டும் இணையாக்கிலிருந்து வரும் படும் ஒளி அலைக்குச் செங்குத்தாக உள்ளவாறு விளிம்பு விளைவுக் கீற்றணியை முப்பட்டக மேடைமீது அமைக்க வேண்டும். முதல் வரிசை விளிம்பு விளைவு பிம்பம், தொலைநோக்கியில் உள்ள கண்ணருகு வில்லையின் செங்குத்துக் குறுக்குக்கம்பியுடன் ஒன்றிணையும் வகையில் தொலை நோக்கியினை ஒரு பக்கமாகச் சுழற்றவேண்டும். தொலைநோக்கி அமைந்துள்ள நிலைக்கான குறித்துக்கொள்ள வேண்டும்.

இதேபோன்று மற்றொரு பக்கமாக தொலைநோக்கியைச் சுற்றி முதல்வரிசை விளிம்பு விளைவு பிம்பம் செங்குத்துக் குறுக்குக்கம்பியுடன் ஒன்றினையும் வகையில் அமைத்து அளவீடுகளைக் குறித்துக் கொள்ள வேண்டும். இரண்டு நிலைகளுக்கும் இடையே உள்ள வேறுபாடு 2θ வைக் கொடுக்கும். இதன் மதிப்பில் பாதி, முதல் வரிசை பெருமத்திற்கான விளிம்பு விளைவுக் கோணத்தைக் கொடுக்கும் (θ) இது படம் 6.67 -இல் காட்டப்பட்டுள்ளது. ஒளியின் அலைநீளம் பின்வரும் சமன்பாட்டினால் கணக்கிடப்படுகிறது.

இங்கு N என்பது ஒரு மீட்டர் நீளத்தில் வரையப்பட்ட கோடுகளின் எண்ணிக்கையாகும். மேலும் m என்பது விளிம்பு விளைவு பிம்பத்தின் வரிசையாகும்.

கண்கவர் வண்ணங்களில் குறுந்தகடுகள் (Compact disc) தோன்றுவதை நீங்கள் பார்த்திருக்கிறீர்களா? பதிவு செய்யப்பட்டிருக்கும் பளபளப்பான பக்கத்தில் வட்ட வடிவ குறுகிய வெட்டுகள் காணப்படும். இவ்வெட்டுகளின் அகலம் கண்ணுறு ஒளியின் அலைநீளத்துடன் ஒப்பிடத்தக்க அளவில் உள்ளதால், கண்ணுறு ஒளி அலைகள் குறுந்தகடுகளின் இப்பக்கத்தின் மீது பட்டு எதிரொளிக்கும்போது விளிம்பு விளைவு ஏற்பட்டுக் கண்கவர் வண்ணங்களில் குறுந்தகடுகள் தோன்றுகின்றன. பாடல்கள் மற்றும் படங்கள் பதிவு செய்யப்பட்டிருக்கும் பிளவுகள் விளிம்பு விளைவுக் கீற்றணி போன்று செயல்படுகின்றன.

8. வெவ்வேறு வண்ண ங்களின் அலைநீளங்களைக் கண்டறிதல்

வெள்ளை ஒளியைப் பயன்படுத்தும்போது, மையப்பொலிவின் இரண்டு பக்கங்களிலும் தொடர்ச்சியான வண்ண விளிம்பு விளைவுப்பட்டைகள் தோன்றும். மையப்பெருமம் வெண்மை நிறத்திலும், அனைத்து வண்ணங்களும் எவ்வித பாதை வேறுபாடும் இன்றி, ஒன்றை ஒன்று வலுவூட்டும் வகையில் ஒன்றிணையும். θ அதிகரிக்கும்போது, பாதை வேறுபாடு (a+b) sinθ ஊதாமுதல் சிவப்புவரை உள்ள அனைத்து வண்ணங்களின் பெரும விளிம்பு விளைவு நிபந்தனைகளின் வழியே கடந்து செல்லும். இது படம் 6.68-இல் காட்டியுள்ளவாறு மையப்பொலிவின் இரண்டுப்பக்கங்களிலும் ஊதா முதல் சிவப்புவரையுள்ள நிறமாலை உருவாக்கும். வெவ்வேறு வரிசைகளைக் கொண்ட விளிம்புவிளைவுக் கோணங்களைக் கண்டறிந்து, வண்ணங்களின் அலைநீளங்களைப் பின்வரும் சமன்பாட்டினைப் பயன்படுத்திக் கணக்கிடலாம்.

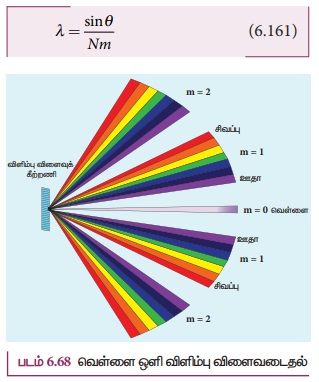
இங்கு N என்பது கீற்றணியில் ஒரு மீட்டர் நீளத்தில் வரையப்பட்ட கோடுகளின் எண்ணிக்கையையும், m என்பது விளிம்பு விளைவு பிம்பத்தின் வரிசையையும் குறிக்கும்.

9. பிரித்தறிதல் (Resolution)

நுண்ணோக்கி மற்றும் தொலை நோக்கி போன்ற ஒளியியல் கருவிகளில் தோன்றும் பிம்பங்களில் ஏற்படும் விளிம்பு விளைவு விரும்பத்தகாத ஒன்றாகும். ஒற்றைப்பிளவில் மையப்பொலிவு ஏற்படுத்தும் அரைக்கோணம் θ (அல்லது முதல் சிறுமத்தின் நிலை) பின்வரும் சமன்பாட்டினால் வழங்கப்படுகிறது.

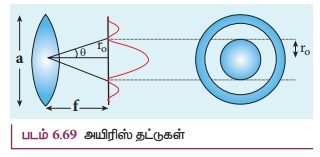
ஒற்றைப்பிளவு போன்றே, வட்ட வடிவத்துளை ஒன்று (லென்ஸ் அல்லது கருவிழி போன்றவை) புள்ளிப்பொருளின் பிம்பத்தை ஏற்படுத்தும்போது, அப்பிம்பம் புள்ளிப்பொருள் போன்று தோன்றாமல் படம் 6.69-இல் காட்டியுள்ளவாறு மையத்தைவிட்டு விலகிச்செல்லும் போது ஒரு மைய வளையங்களுடன் மங்கலாகத் தெரியும். இவற்றுக்கு அயிரிஸ் தட்டுகள் (Airys discs) என்று பெயர். மையப் பெரும வட்டத்தின் அரைக் கோணப்பரவல் பின்வரும் சமன்பாட்டினால் வழங்கப்படுகிறது.

இங்கு 1.22 என்ற எண்மதிப்பு வட்டத்துளை ஏற்படுத்திய மையப் பெருமத்தினால் ஏற்படுகிறது. இதனை விளக்குவதற்கு உயர் கணிதம் தேவைப்படுவதால் இதனைப்பற்றி உயர்வகுப்புகளில் படிக்கலாம்.

சிறிய கோணங்களுக்கு ,

சமன்பாட்டினை மேலும் மாற்றியமைக்கும் போது,

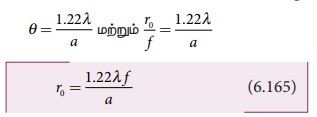
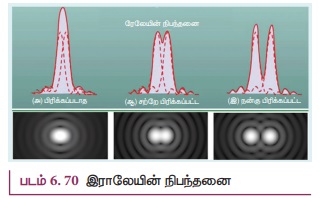
அருகருகே அமைந்துள்ள புள்ளி ஒளிமூலங்களினால் ஏற்படும் பிம்பங்களின் விளிம்பு விளைவு அமைப்புகள் ஒன்றுடன் ஒன்று மேற்பொருந்தி, படம் 6.70 (அ) இல் காட்டியுள்ளவாறு மங்கலான பிம்பத்தைத் திரையில் தோற்றுவிக்கும். இரண்டு ஒளிமூலங்களின் பிம்பங்களைச் சிறப்பாகப் பெறுவதற்கு, இரண்டு புள்ளி ஒளிமூலங்களும் நன்கு பிரித்தறியப்பட்டிருக்க வேண்டும். அதாவது, இரண்டு புள்ளி ஒளிமூலங்களின் பிம்பங்கள் ஒன்றுடன் ஒன்று மேற்பொருந்தா வண்ணம் பிரிக்கப்பட்டிருக்கவேண்டும். இராலேயின் (Rayleigh's) நிபந்தனையின்படி இரண்டு புள்ளி ஒளிமூலங்கள் நன்கு பிரித்தறியப்பட வேண்டுமெனில், அவ்விரண்டு ஒளி மூலங்களின் விளிம்பு விளைவு பின்வருமாறு அமைய வேண்டும். அதாவது முதல் பிம்பத்தின் மையப் பெருமம், இரண்டாவது பிம்பத்தின் முதல் சிறுமத்துடன் ஒன்றிணைய வேண்டும். இதேபோன்று, இரண்டாவது பிம்பத்தின் மையப் பெருமம், முதல் பிம்பத்தின் முதல் சிறுமத்துடன் ஒன்றிணைய வேண்டும். இவ்வாறு ஏற்படும் பிம்பங்கள், பொருளின் பிரித்தறியப்பட்ட பிம்பங்கள் என அழைக்கப்படும். இராலேயின் நிபந்தனையைப் பிரித்தறிதலின் எல்லை என்றும் அழைக்கலாம்.

இராலேயின் நிபந்தனையின்படி, இரண்டு புள்ளி ஒளி மூலங்கள் பிரித்தறியப்பட வேண்டுமெனில், அவற்றின் பிம்பங்களுக்கிடைப்பட்ட தொலைவு குறைந்தப்பட்சம் r₀ தொலைவு இருக்க வேண்டும். கோணப் பிரித்தறிதலின் அலகு ரேடியன் (rad). மேலும், இது பின்வரும் சமன்பாட்டால் வழங்கப்படுகிறது

சிறப்பான பிரித்தறிதலுக்கு முதல் வரிசை விளிம்பு விளைவுக் கோணம் மிகச்சிறியதாக இருக்க வேண்டும். மேலும், பயன்படுத்தப்படும் ஒளியின் அலை நீளம் சிறியதாக இருக்க வேண்டும் மற்றும் பயன்படுத்தப்படும் கருவியின் துளையின் அளவு பெரியதாக இருக்க வேண்டும். சமன்பாடு 6.165 இடம்சார் பிரித்தறிதலைக் கணக்கிடப் பயன்படுகிறது.

பிரித்தறிதலின் தலைகீழிக்குப் பிரிதிறன் என்று பெயர். இதிலிருந்து கருவியின் சிறிய பிரித்தறிதல் பெரிய பிரிதிறனைக் கொடுக்கும் என அறியலாம். பிம்பங்களைத் தோற்றுவிப்பதன் மூலம், மிகச்சிறிய அல்லது அருகருகே உள்ள பொருள்களைப் பிரித்துப் பார்க்கும் அல்லது வேறுபடுத்திப் பார்க்கும் திறமைக்கு ஒளியியல் கருவியின் பிரிதிறன் என்று பெயர். பொதுவாகப் பிரித்தறிதல் என்ற சொல் உருவாகும் பிம்பத்தின் தரத்தையும், பிரிதிறன் என்பது ஒளியியல் கருவியின் பிரித்தறியும் திறமையையும் குறிக்கும்.

எடுத்துக்காட்டு 6.36

காவலூரில் அமைந்துள்ள வைனு பாப்பு (Vainu Bappu) வானியல் ஆய்வு மையத்தில் உள்ள பொருளருகு லென்சின் விட்டம் 2.3 m. 589 nm அலைநீளம் கொண்ட ஒளியினைப் பயன்படுத்தினால் கிடைக்கும் கோணப் பிரிதிறனைக் காண்க.

தீர்வு

பொருளருகு லென்சின் விட்டம் a = 2.3 m;

ஒளியின் அலைநீளம்λ = 589 nm = 589x10^-9 m;

θ= ?

கோணப் பிரிதிறனுக்கான சமன்பாடு,

θ =1.227λ/a

மதிப்புகளைப் பிரதியிடும் போது,

θ = 1.22 X 589 x 10^-9 / 2.3 = 321.4X10^-9

θ = 3.214 x 10^-7 rad ≈ 0.0011’

குறிப்பு: மனிதக் கண்களின் கோணப் பிரிதிறனின் மதிப்பு, தோராயமாக 3X10^-4 rad ≈ 1.03'.