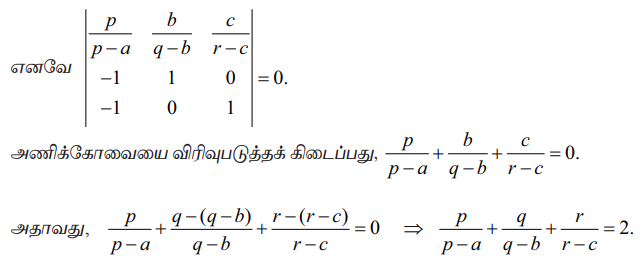சமபடித்தான நேரியச் சமன்பாடுகளின் தொகுப்பு (Homogeneous system of linear equations)

2. சமபடித்தான நேரியச் சமன்பாடுகளின் தொகுப்பு 

(Homogeneous system of linear equations)

ஒரு நேரியச் சமன்பாட்டுத் தொகுப்பானது

a11 x1 + a12 x2 + a13 x3 + ... + a1n xn = 0,

a21 x1 + a22 x2 + a23 x3 + ... + a2n xn = 0,

...  ...  ... ... ... ...     

am1 x1 + am2 x2 + am3 x3 + ... + amn xn = 0,

... (1) 

என்பதாகும் என்பதை நினைவுகூர்வோம்.

இங்கு aij, i = 1, 2, ..., m; j = 1, 2, ..., n என்பவை மாறிலிகள். இத்தொகுப்பில் உள்ள சமன்பாடுகள் x1 = 0, x2 = 0, xn = 0 என்ற மதிப்புகளுக்கு நிறைவடைகின்றன. இத்தீர்வை வெளிப்படைத் தீர்வு என்கிறோம். இத்தொகுப்பானது எப்பொழுதும் ஒருங்கமைவு உடையதாகும்.

மேல் உள்ள தொகுப்பை AX = Om × 1, என்ற அணிவடிவில் எழுதலாம். இங்கு

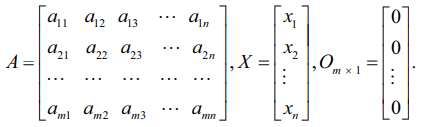
Om × 1 −ஐ O என்ற ஆங்கில எழுத்தால் குறிப்பிடுகின்றோம். O என்பது பூச்சிய நிரல் அணி என்பதால் ρ(A) = ρ ([A | O]) ≤ m என்பது எப்பொழுதும் மெய்யாக இருக்கும். எனவே சமபடித்தான நேரியச் சமன்பாட்டுத் தொகுப்பானது எப்பொழுதும் ஒருங்கமைவு உடையதாகும். m < n, எனில் மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை சமன்பாடுகளின் எண்ணிக்கைக்கு அதிகமாக இருக்கும். எனவே ρ(A) = ρ ([A | O]) < n. தொகுப்பு (1) ஆனது வெளிப்படையற்ற (non −  trivial) தீர்வைப் பெற்றிருக்கும்.

m = n, எனில் மதிப்பிடவேண்டிய மாறிகளின் எண்ணிக்கையானது சமன்பாடுகளின் எண்ணிக்கைக்குச் சமம். எனவே, தொகுப்பானது

a11 x1 + a12 x2 + a13 x3 + ... + a1n xn = 0,

a21 x1 + a22 x2 + a23 x3 + ... + a2n xn = 0,

...  ...  ... ... ... ...     

an1 x1 + an2 x2 + an3 x3 + ... + ann xn = 0

... (2)

என அமையும். இதில் இரு வகைகள் உள்ளன.

வகை (i)

ρ (A) = ρ ([A | O]) = n, எனில் தொகுப்பு (2) ஆனது ஒரே ஒரு தீர்வைப் பெற்றிருக்கும். அத்தீர்வு வெளிப்படைத் (trivial) தீர்வாகும். இங்கு ρ (A) = n என்பதால், | A| ≠  0. எனவே வெளிப்படைத் தீர்விற்கு |A| ≠ 0.

வகை (ii)

ρ (A) = ρ ([A | O]) < n, எனில் தொகுப்பு (2) ஆனது வெளிப்படையற்ற (non−trivial) தீர்வைப் பெற்றிருக்கும். இங்கு ρ (A) < n என்பதால், |A| = 0. எனவே சமப்படித்தான நேரியச் சமன்பாட்டுத் தொகுப்பானது வெளிப்படையற்ற தீர்வு பெற்றிருந்தால், மற்றும் பெற்றிருந்தால் மட்டுமே அணியின் அணிக்கோவை மதிப்பு பூச்சியமாக இருக்கும்.

m > n, எனில் மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கையை விட சமன்பாடுகளின் எண்ணிக்கை அதிகமாக இருக்கும். இந்நிலையில் தொடக்கநிலை உருமாற்றங்கள் மூலம் ρ (A) = ρ ([A | O]) ≤ n எனப்பெறலாம்.

எடுத்துக்காட்டு 1.35

பின்வரும் சமன்பாட்டுத் தொகுப்பைத் தீர்க்கவும்:

x + 2y + 3z = 0, 3x + 4y + 4z = 0, 7x + 10y + 12z = 0.

தீர்வு

இங்கு சமன்பாடுகளின் எண்ணிக்கையும், மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கையும் சமம். விரிவுபடுத்தப்பட்ட அணியை ஏறுபடி வடிவத்திற்கு மாற்ற (காஸ்ஸியன் நீக்கல் முறை) கிடைப்பது

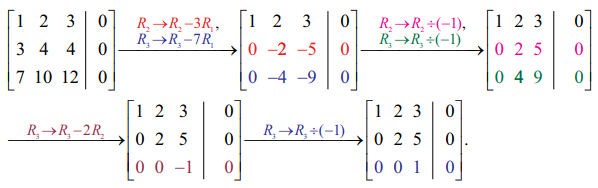
ρ (A) = ρ ([A | O]) = 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை.

எனவே தொகுப்பிற்கும் x = 0, y = 0, z = 0 என்ற ஒரே ஒரு வெளிப்படைத் தீர்வு மட்டும்தான் உண்டு.

குறிப்பு

மேல் உள்ள எடுத்துக்காட்டில்

|A| = = 1 (48 – 40) – 2 (36 – 28) + 3 (30 − 28) = 8 − 16 + 6 = −2 ≠ 0 என்பதை நாம் காணலாம்.

எடுத்துக்காட்டு 1.36

x + 3y − 2z = 0, 2x – y + 4z = 0, x −11y + 14z = 0 என்ற சமன்பாட்டுத் தொகுப்பைத் தீர்க்கவும்.

தீர்வு

மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை 3.

விரிவுபடுத்தப்பட்ட அணியை ஏறுபடி வடிவத்திற்கு மாற்ற (காஸ்ஸியன் நீக்கல் முறை) கிடைப்பது

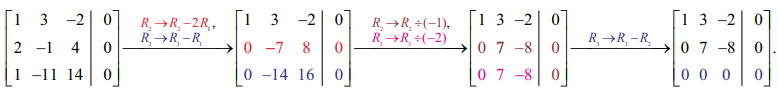
ρ (A) = ρ ( [A | O] ) = 2 < 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை.

தொகுப்பானது ஒரு சாராமாறிக் குடும்பத் தீர்வுகள் பெற்றிருக்கும்.

ஏறுபடி வடிவத்தின் நமக்குக் கிடைக்கும் சமன்பாடுகளாவன

x + 3y − 2z = 0, 7y − 8z = 0, 0 = 0.

z = t என்க. இங்கு t என்பது மெய் எண் உடைய தன்னிச்சை மாறி. பின்னோக்கிப் பிரதியிடல் முறையில் கிடைப்பது 

z = t,

7y − 8t = 0 ⇒ y = 8t / 7,

x + 3 (8t / 7) − 2t = 0 ⇒ x + ( (24t − 14t) / 7) 0 ⇒ x = − (10t / 7). 

எனவே தீர்வானது (x = − (10t / 7), y = 8t / 7, z = t ). இங்கு t என்பது ஒரு மெய்யெண்.

எடுத்துக்காட்டு 1.37

பின்வரும் தொகுப்பைத் தீர்க்கவும்:

x + y − 2z = 0, 2x − 3y + z = 0, 3x − 7y + 10z = 0, 6x − 9y + 10z = 0.

தீர்வு

இங்கு சமன்பாடுகளின் எண்ணிக்கை 4 மற்றும் மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை 3. விரிவுபடுத்தப்பட்ட அணியை ஏறுபடி வடிவிற்கு மாற்றக் கிடைப்பது

எனவே ρ (A) = ρ ([A | O]) = 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை. ஆதலால், தொகுப்பிற்கு வெளிப்படைத் தீர்வு மட்டும்தான் உண்டு.

எடுத்துக்காட்டு 1.38

பின்வரும் தொகுப்பானது வெளிப்படையற்ற தீர்வு பெற்றிருக்குமாயின் λ −ன் மதிப்பு காண்க. 

(3λ − 8)x + 3y + 3z = 0, 3x + (3λ − 8)y + 3z = 0, 3x + 3y + (3λ − 8)z = 0

தீர்வு

தொகுப்பானது வெளிப்படையற்றத் தீர்வு பெற்றிருப்பதால் கெழுக்களின் அணியின் அணிக்கோவை மதிப்பு பூச்சியமாகும்.

ஆதலால் நமக்குக் கிடைப்பது

= 0 அல்லது

அல்லது (3λ − 2) (3λ − 11)2 0. எனவே λ = 2 / 3 மற்றும் λ = 11 / 3.

இப்பொழுது நாம் நேரியச் சமப்படித்தான சமன்பாட்டுத் தொகுப்பை வேதியியலில் பயன்படுத்த உள்ளோம். வேதியியல் சமன்பாட்டின் இருபக்கங்களிலும் உள்ள அணுக்களின் எண்ணிக்கையை ஆய்வு செய்வதன் மூலம் வேதியியல் எதிர்வினைச் சமன்பாடுகளைச் சமநிலைப்படுத்துவது பற்றி ஏற்கனவே அறிந்துள்ளோம். இதற்கான ஒரு நேரடி முறையை பின்வரும் எடுத்துக்காட்டு மூலம் விளக்குவோம்.

எடுத்துக்காட்டு 1.39

காஸ்ஸியன் நீக்கல் முறையைப் பயன்படுத்தி பின்வரும் வேதியியல் எதிர்வினைச் சமன்பாட்டை சமநிலைப்படுத்துக:

C5H8 + O2 → CO2 + H2O

(மேற்காணும் எதிர்வினையானது, ஐசோபிரீன் (Isoprene) என்ற கரிம வேதியியல் கூட்டுப் பொருளை எரிப்பதால் நிகழ்வதாகும்).

தீர்வு

நாம் x1, x2, x3 மற்றும் x4 என்ற மிகை முழுக்களை

x1C5H8 +  x2O2 = x3CO2 +  x4H2O என அமையுமாறு காண விழைகிறோம்... (1)

(1) −ன் இடதுபுறத்திலுள்ள கார்பன் அணுக்களின் எண்ணிக்கை (1) −ன் வலதுபுறத்திலுள்ள கார்பன் அணுக்களின் எண்ணிக்கைக்குச் சமமாக இருக்க வேண்டும். எனவே,

5x1 = x3 ⇒ 5x1  − x3 = 0 ... (2)

என்ற நேரியச் சமப்படித்தான சமன்பாட்டைப் பெறுகிறோம். இதேபோல் ஹைட்ரஜன் மற்றும் ஆக்ஸிஜன் அணுக்கள் எண்ணிக்கைகளை ஒப்பிடக் கிடைப்பது,

8x1 = 2x4 ⇒ 4x1 – x4 = 0,     ... (3)

2x2 = 2x3 + x4  ⇒ 2x2 − 2x3 − x4 = 0.     ... (4)

சமன்பாடுகள் (2), (3), மற்றும் (4) என்பன 4 மாறிகளில் 

ஒரு நேரியச் சமப்படித்தான தொகுப்பை ஏற்படுத்துகின்றன.

விரிவுபடுத்தப்பட்ட அணியானது, [A | B] =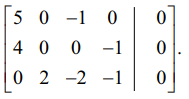

காஸ்ஸியன் நீக்கல் முறையை பயன்படுத்த,

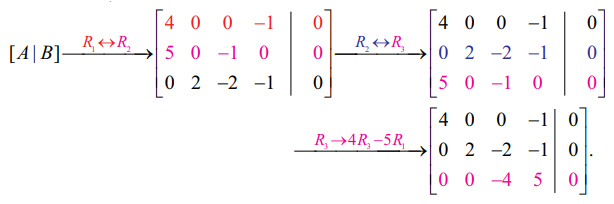
எனவே, ρ (A) = ρ ([A | B]) = 3 < 4 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை.

தொகுப்பானது ஒருங்கமைவு உடையது மற்றும் எண்ணற்ற தீர்வுகளைப் பெற்றிருக்கும். 

ஏறுபடி வடிவத்தில் நமக்குக் கிடைக்கும் சமான சமன்பாடுகள்

4x1 – x4 = 0, 2x2 – 2x3 – x4 = 0, –4x3 + 5x4 = 0. 

எனவே ஒரு மாறியை பூச்சியமற்ற மெய் எண் பெறும் தன்னிச்சை மாறியாக எடுத்துக் கொள்ள வேண்டும்.

x4 = t, t ≠ 0  என்க. பின்னோக்கிப் பிரதியிடல் முறையில் x3 = 5t / 4, x2 =7t / 4, x1 = t / 4 எனப் பெறுகிறோம்.

x1, x2, x3 மற்றும் x4 என்பன மிகை முழுக்கள். எனவே t = 4 எனத் தேர்வு செய்கிறோம். எனவே, x1 = 1, x2 = 7, x3 = 5 மற்றும் x4 = 4 எனக் கிடைக்கிறது. எனவே சமனாமாக்கப்பட்டச் சமன்பாடு, C5H8 + 7O2 → 5CO2 + 4H2O ஆகும்.

எடுத்துக்காட்டு 1.40

px + by + cz = 0, ax + qy + cz = 0, ax + by + rz = 0 என்ற சமன்பாடுகளின் தொகுப்பு வெளிப்படையற்றத் தீர்வு பெற்றுள்ளது மற்றும் p ≠ a, q ≠ b, r ≠ c, எனில் 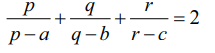 என நிறுவுக.

தீர்வு

px + by + cz = 0, ax + qy + cz = 0, ax + by + rz = 0 என்ற தொகுப்பின் சமன்பாடுகள் வெளிப்படையற்றத் தீர்வு பெற்றுள்ளது என்க.

எனவே 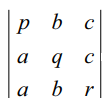  = 0. R2 → R2 – R1 மற்றும் R3 → R3 – R1 என மேல் உள்ள சமன்பாட்டில் பயன்படுத்தக் கிடைப்பது

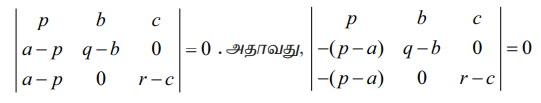
p ≠ a, q ≠ b, r ≠ c, ஆதலால் நாம் பெறுவது, (p – a) (q – b) (r – c) 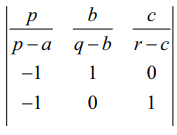  = 0