வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் | பூச்சியமற்ற கோவை அணியின் நேர்மாறு (Inverse of a Non−Singular square matrix) - அசமப்படித்தான நேரியச் சமன்பாடுகள் (Non – homogeneous Linear Equation) | 12th Maths : UNIT 1 : Applications of Matrices and Determinants
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 1 : அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள்
அசமப்படித்தான நேரியச் சமன்பாடுகள் (Non – homogeneous Linear Equation)
அணிகளின் பயன்பாடுகள்: நேரியச் சமன்பாடுகளின் தொகுப்பிற்குரிய ஒருங்கமைவுத் தன்மையைத் தரம் மூலம் காணல்
(Applications of Matrices: Consistency of System of Linear Equations by Rank Method)
பகுதி 1.4.3 இல் நாம் நேரியச் சமன்பாட்டுத் தொகுதிகளின் ஒருங்கமைவுத் தன்மையைப் பற்றி வரையறுத்துள்ளோம். இப்பாடப்பகுதியில் இதை அணித்தரம் மூலம் ஆராய உள்ளோம். பின்வரும் தேற்றத்தை நிரூபணமின்றி பயிலுவோம்:
தேற்றம் 1.14 (ரூச்சி − கபெல்லி தேற்றம்) (Rouche – Capelli Theorem)
AX = B என்ற அணி வடிவத்திலுள்ள நேரியச் சமன்பாடுகளின் தொகுப்பானது ஒருங்கமைவு உடையதற்குப் போதுமான மற்றும் தேவையான நிபந்தனையாதெனில் கெழுக்கள் அணியின் தரமும் மற்றும் விரிவுபடுத்தப்பட்ட அணியின் தரமும் சமமாக இருக்க வேண்டும். அதாவது ρ(A) = ρ ([A| B]).
மேற்காணும் தேற்றத்தினைப் பின்வரும் எடுத்துக்காட்டுகளில் பயன்படுத்துவோம்.
1. அசமப்படித்தான நேரியச் சமன்பாடுகள்
(Non – homogeneous Linear Equation)
எடுத்துக்காட்டு 1.29
பின்வரும் நேரியச் சமன்பாடுகளின் தொகுப்பானது ஒருங்கமைவு உடையதா என ஆராய்க. ஒருங்கமைவு உடையதாயின் அவற்றைத் தீர்க்க:
x + 2y − z = 3, 3x – y + 2z = 1, x − 2y + 3z = 3, x – y + z + 1 = 0.
தீர்வு
இங்கு மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை 3.
தொகுப்பின் அணி வடிவம் AX = B, இங்கு

[A | B] −ல் காஸ்ஸியன் நீக்கல் முறையை பயன்படுத்தக் கிடைப்பது

விரிவுபடுத்தப்பட்ட அணி [A | B] −ல் மூன்று அபூச்சிய நிரைகள் உள்ளன.
எனவே, ρ ([A | B]) = 3.
A −யின் நிரை − ஏறுபடி வடிவமானது 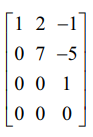 இதில் மூன்று அபூச்சிய நிரைகள் உள்ளன.
இதில் மூன்று அபூச்சிய நிரைகள் உள்ளன.
எனவே, ρ (A) = 3.
எனவே, ρ (A) = ρ ([A | B]) = 3.
ஏறுபடி வடிவத்திலுள்ள அணியிலிருந்து கிடைக்கும் சமான சமன்பாடுகளின் தொகுப்பானது x + 2y − z = 3, 7y − 5z = 8, z = 4, 0 = 0.
கடைசி சமன்பாடு 0 = 0 என்பது அர்த்தமுள்ளது. பின்னோக்கிப் பிரதியிடல் முறையில் நமக்குக் கிடைப்பது
z = 4
7y – 20 = 8 ⇒ y = 4,
x = 3 – 8 + 4 ⇒ x = −1.
எனவே தீர்வானது (x = –1, y = 4, z = 4). (இங்கு A −ஆனது சதுர அணியல்ல என்பது குறிப்பிடத்தக்கது)
இங்கு தொகுப்பானது ஒருங்கமைவு உடையது. ஒரே ஒரு தீர்வைப் பெற்றுள்ளது.
எடுத்துக்காட்டு 1.30
பின்வரும் நேரியச் சமன்பாடுகளின் தொகுப்பானது ஒருங்கமைவு உடையதா என ஆராய்க. ஒருங்கமைவு உடையதாயின் அவற்றைத் தீர்க்க:
4x − 2y + 6z = 8, x + y − 3z = −1, 15x − 3y + 9z = 21.
தீர்வு
மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை 3.
தொகுப்பின் அணி வடிவம் AX = B.
இங்கு 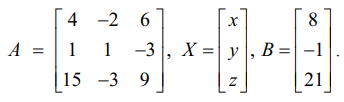
[A | B] என்ற விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரை செயலிகள் பயன்படுத்தக் கிடைப்பது

எனவே ρ (A) = ρ ([A | B]) = 2 < 3.
ஏறுபடி வடிவத்திலுள்ள அணியிலிருந்து கிடைக்கும் சமான சமன்பாடுகளின் தொகுப்பானது
x + y − 3z = −1, y − 3z = −2, 0 = 0.
இதில் கடைசி சமன்பாடு 0 = 0 வெளிப்படையானது மற்றும் பொருத்தமுடையது.
மேலும் வெளிப்படையற்ற சமன்பாடுகள் இரண்டு உள்ளன. மூன்று தொகுப்பில் மாறிகள் உள்ளன. எனவே மாறிகளில் ஒன்றை நமது விருப்பப்படி நிலை நிறுத்தி மற்ற இரு மாறிகளுக்கான இரு சமன்பாடுகளைப் பெறலாம். எனவே z −ஐ t என்ற மெய்யெண் பெறும் தன்னிச்சை மாறியாகக் கொள்வோம். எனவே நாம் பெறுவது y = 3t − 2, x = −1 − (3t − 2) + 3t = 1. எனவே தீர்வானது (x = 1, y = 3t − 2, z = t) ஆகும். இங்கு t என்பது தன்னிச்சை மெய்யெண் ஆகும். மேல் உள்ள தீர்வுக் கணமானது ஒரு சாராமாறி குடும்பத் தீர்வுகள் ஆகும். எனவே கொடுத்துள்ள தொகுப்பானது ஒருங்கமைவுடையது மற்றும் எண்ணற்ற தீர்வுகள் பெற்றிருக்கும். இந்த எண்ணற்ற தீர்வுகள் ஒரு குடும்பத் தீர்வுகளாகும்.
குறிப்பு
மேல் உள்ள எடுத்துக்காட்டில் சதுர அணி A யானது பூச்சியக்கோவை அணியாகும். ஆதலால் நேர்மாறு அணி காணல் முறையிலோ அல்லது கிராமர் விதியைப் பயன்படுத்தியோ தொகுப்புகளில் உள்ள சமன்பாடுகளைத் தீர்க்க இயலாது. இருப்பினும் காஸ்ஸியன் நீக்கல் முறையைப் பயன்படுத்த முடியும் மற்றும் தொகுப்பானது ஒருங்கமைவு உடையதா அல்லது ஒருங்கமைவு அற்றதா எனத் தீர்மானிக்கலாம். அடுத்த எடுத்துக்காட்டு மற்ற முறைகள் மீது காஸ்ஸியன் நீக்கல் முறையின் மேலாதிக்கத்தை உறுதிப்படுத்துகிறது.
எடுத்துக்காட்டு 1.31
பின்வரும் நேரியச் சமன்பாடுகளின் தொகுதியின் ஒருங்கமைவினைச் சோதிக்கவும், மற்றும் இயலுமாயின் தீர்க்கவும்.
x − y + z = −9, 2x − 2y + 2z = −18, 3x − 3y + 3z + 27 = 0.
தீர்வு
இங்கு மதிப்பிடப்பட வேண்டிய மாறிகளின் எண்ணிக்கை 3.
தொகுப்பின் அணி வடிவம் AX = B, இங்கு
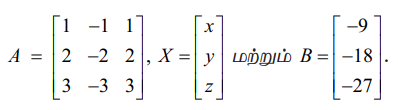
[A | B] என்ற விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரைச் செயலிகளைப் பயன்படுத்தக் கிடைப்பது
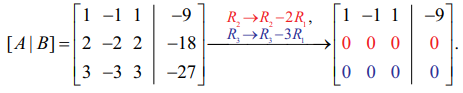
எனவே ρ(A) = ρ ([A | B]) = 1 < 3.
ஏறுபடி வடிவத்திலுள்ள அணியிலிருந்து கிடைக்கும் சமான சமன்பாடுகளின் தொகுப்பானது x – y + z = −9, 0 = 0, 0 = 0.
முரண்பாடான முடிவுகள் கிடைக்கப் பெறாமையினால், தரப்பட்டத் தொகுப்பு பொருத்தமுடையது. இங்கு ஒரு வெளிப்படையற்ற சமன்பாடு மட்டுமே உள்ளது மற்றும் தொகுப்பிற்கு 3 மாறிகள் உள்ளன.
y = s, z = t என தன்னிச்சையாக எடுத்துக்கொள்ள நமக்குக் கிடைப்பது x – s + t = −9; அல்லது x = −9 + s − t.
எனவே தீர்வானது (x = −9 + s − t, y = s, z = t), இங்கு s மற்றும் t என்பன மெய்யெண் சாராமாறிகள் (parameters)
மேல் உள்ள தீர்வுக்கணம் இரு சாராமாறிக் குடும்பத் தீர்வுகளாக அமைகின்றன.
இங்கு தொகுப்பானது ஒருங்கமைவு உடையது மற்றும் எண்ணற்ற தீர்வுகளைப் பெற்றுள்ளது. இத்தீர்வுகள், இரு சாராமாறிக் குடும்பத் தீர்வுகளாக இருக்கின்றன.
எடுத்துக்காட்டு 1.32
பின்வரும் நேரியச் சமன்பாட்டுத் தொகுப்பானது ஒருங்கமைவு உடையதா என ஆராய்க.
x − y + z = −9, 2x − y + z = 4, 3x – y + z = 6, 4x – y + 2z = 7.
தீர்வு
இங்கு மதிப்பிடப்பட வேண்டிய மாறிகளின் எண்ணிக்கை 3.
தொகுப்பின் அணி வடிவம் AX = B, இங்கு
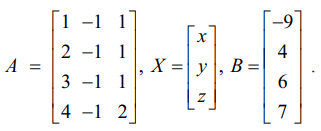
[A | B] என்ற விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரைச் செயலிகள் பயன்படுத்தக் கிடைப்பது,

எனவே ρ(A) = 3 மற்றும் ρ ([A | B]) = 4. எனவே ρ(A) ≠ ρ ([A | B]).
ஏறுபடி வடிவத்திலுள்ள அணியிலிருந்து கிடைக்கும் சமான சமன்பாடுகளின் தொகுப்பானது x − y + z = −9, y – z = 22, z = −23, 0 = −11.
கடைசி சமன்பாடானது முரண்பாடாக உள்ளது. எனவே கொடுக்கப்பட்ட சமன்பாடுகளின் தொகுப்பானது ஒருங்கமைவற்றது மற்றும் தொகுப்பிற்கு தீர்வு கிடையாது.
ரூச்சி − கபெல்லி (Rouche − Capelli) தேற்றத்தினால் பின்வரும் விதியைப் பெறுகிறோம்:
∙ தொகுப்பில் உள்ள சமன்பாடுகளில் மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை n மற்றும் ρ(A) = p ([A | B]) = n, எனில் AX = B என்ற தொகுப்பானது ஒருங்கமைவு உடையது மற்றும் தொகுப்பிற்கு ஒரே ஒரு தீர்வுதான் உண்டு.
∙ AX = B என்ற தொகுப்பில் மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை n மற்றும் ρ(A) = ρ ([A | B]) = n − k, k ≠ 0 எனில் தொகுப்பானது ஒருங்கமைவு உடையது மற்றும் எண்ணற்றதீர்வுகளைப் பெற்றிருக்கும். இத்தீர்வுகள் k − சாராமாறிக் குடும்பமாக (k− parameter family) இருக்கும். எடுத்துக்காட்டாக தொகுப்பில் உள்ள சமன்பாடுகளில் 3 மதிப்பிட வேண்டிய மாறிகள் மற்றும் ρ(A) = ρ ([A | B]) = 2, எனில் தொகுப்பானது எண்ணற்ற தீர்வுகள் பெற்றிருக்கும் மற்றும் இத்தீர்வுகள் ஒரு சாராமாறிக் குடும்பமாக (one parameter family) இருக்கும். இதேபோல் தொகுப்பில் உள்ள சமன்பாடுகளில் மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை 3 ஆகவும் மற்றும் ρ (A) = ρ ([A | B]) = 1, எனில் தொகுப்பானது ஒருங்கமைவு உடையது மற்றும் எண்ணற்ற தீர்வுகளைப் பெற்றிருக்கும். இத்தீர்வுகள் இரு சாராமாறிக் குடும்பமாக (two parameter family) இருக்கும்.
∙ ρ (A) ≠ ρ ([A | B]), எனில் AX = B என்ற தொகுப்பானது ஒருங்கமைவற்றது மற்றும் தொகுப்பிற்குத் தீர்வு கிடையாது.
எடுத்துக்காட்டு 1.33
x + y + z = a, x + 2y + 3z = b, 3x + 5y + 7z = c என்ற நேரியச் சமன்பாடுகளின் தொகுப்பின் தீர்வுகள் ஒரு சாராமாறிக் குடும்பமாக இருப்பதற்கு a, b மற்றும் c −ல் உருவாகும் நிபந்தனையைக் காண்க.
தீர்வு
இங்கு மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை 3.
தொகுப்பின் அணி வடிவம் AX = B, இங்கு 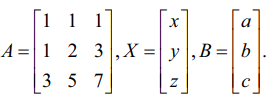
[A | B] என்ற விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரைச் செயலிகள் பயன்படுத்தக் கிடைப்பது,
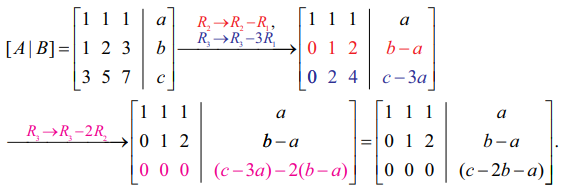
தொகுப்பின் தீர்வுகள் ஒரு சாராமாறிக் குடும்பமாக இருக்க வேண்டுமாயின்,
ρ (A) = p ([A,B]) = 2. எனவே ஏறுபடி வடிவத்திலுள்ள மூன்றாவது நிரையானது பூச்சிய நிரையாக இருக்க வேண்டும்.
எனவே, c – 2b – a = 0 ⇒ c = a + 2b.
எடுத்துக்காட்டு 1.34
λ, μ −இன் எம்மதிப்புகளுக்கு
x + 2y + z = 7, x + y + λz = μ, x + 3y − 5z = 5
என்ற சமன்பாடுகள் (i) யாதொரு தீர்வும் பெற்றிறாது (ii) ஒரே ஒரு தீர்வைப் பெற்றிருக்கும் (iii) எண்ணிக்கையற்ற தீர்வுகளைப் பெற்றிருக்கும் என்பதனை ஆராய்க.
தீர்வு
மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை 3.
தொகுப்பின் அணி வடிவமானது AX = B, இங்கு 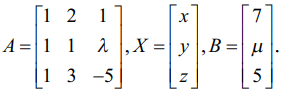
[A | B] என்ற விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரைச் செயலிகள் பயன்படுத்தக் கிடைப்பது
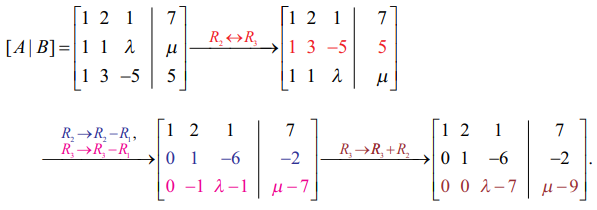
(i) λ = 7 மற்றும் μ ≠ 9, எனில் ρ(A) = 2 மற்றும் ρ ([A | B]) = 3 எனவே ρ (A) ≠ ρ ([A | B]) தொகுப்பானது ஒருங்கமைவற்றது. மேலும் தொகுப்பிற்கு தீர்வு கிடையாது.
(ii) λ ≠ 7 மற்றும் μ ஆனது ஏதாவது ஒரு மெய்யெண் எனில் p(A) = 3 மற்றும் ρ ([A | B]) = 3 எனவே ρ (A) = ρ ([A | B]) = 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை.
எனவே கொடுத்துள்ள தொகுப்பானது ஒருங்கமைவு உடையது மற்றும் ஒரே ஒரு தீர்வினைப் பெற்றிருக்கும்.
(iii) λ = 7 மற்றும் μ = 9, எனில் ρ (A) = 2 மற்றும் ρ ([A | B]) = 2
எனவே ρ (A) = ρ ([A | B]) = 2 < மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை 3.
எனவே தொகுப்பானது ஒருங்கமைவுடையது மற்றும் எண்ணிக்கையற்ற தீர்வுகளைப் பெற்றிருக்கும். இத்தீர்வுகள் ஒரு சாராமாறிக் குடும்பத் தீர்வுகளாக அமைகின்றன.