12 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї : Я«ЁЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«»Я««Я»Ї 4 : Я«еЯ»ЄЯ«░Я»ЇЯ««Я«ЙЯ«▒Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї
Я«еЯ»ЄЯ«░Я»ЇЯ««Я«ЙЯ«▒Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї (Properties of Inverse Trigonometric Functions)
Я«еЯ»ЄЯ«░Я»ЇЯ««Я«ЙЯ«▒Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї (Properties of Inverse Trigonometric Functions)
Я«ЄЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«еЯ»ЄЯ«░Я»ЇЯ««Я«ЙЯ«▒Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«┐Я«▓Я«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«єЯ«░Я«ЙЯ«»Я»ЇЯ«хЯ»ІЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«» Я«еЯ»ЄЯ«░Я»ЇЯ««Я«ЙЯ«▒Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«ЕЯ»ЇЯ««Я»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«јЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»І, Я«ЁЯ«хЯ»ЇЯ«хЯ«┐Я«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»ЂЯ««Я»Ї.
Я«фЯ«БЯ»ЇЯ«фЯ»ЂРѕњI
(i) ╬И Рѕѕ [Рѕњ¤ђ/2, ¤ђ/2] Я«јЯ«ЕЯ«┐Я«▓Я»Ї, sinРѕњ1 (sin ╬И) = ╬И
(ii) ╬И Рѕѕ [0, ¤ђ] Я«јЯ«ЕЯ«┐Я«▓Я»Ї, cosРѕњ1 (cos ╬И) = ╬И
(iii) ╬И Рѕѕ (Рѕњ¤ђ/2, ¤ђ/2) Я«јЯ«ЕЯ«┐Я«▓Я»Ї, tanРѕњ1 (tan ╬И) = ╬И
(iv) ╬И Рѕѕ [Рѕњ¤ђ/2, ¤ђ/2] \ {0} Я«јЯ«ЕЯ«┐Я«▓Я»Ї, cosecРѕњ1 (cosec ╬И) = ╬И
(v) ╬И Рѕѕ [0, ¤ђ] \ { ¤ђ/2} Я«јЯ«ЕЯ«┐Я«▓Я»Ї, secРѕњ1 (sec ╬И) = ╬И
(vi) ╬И Рѕѕ (0, ¤ђ) Я«јЯ«ЕЯ«┐Я«▓Я»Ї, cotРѕњ1 (cot ╬И) = ╬И
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї
Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«БЯ»ЇЯ«Ъ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«ЁЯ«хЯ»ѕЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«░Я«┐Я«» Я«еЯ»ЄЯ«░Я»ЇЯ««Я«ЙЯ«▒Я»Ђ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«ЋЯ«│Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ, (i) sin ╬И = x; ╬И Рѕѕ [Рѕњ¤ђ/2, ¤ђ/2] Я«јЯ«ЕЯ»ЇЯ«Ћ.
Я«јЯ«ЕЯ«хЯ»Є Я«еЯ»ЄЯ«░Я»ЇЯ««Я«ЙЯ«▒Я»Ђ Я«џЯ»ѕЯ«ЕЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ, sin ╬И = x Я««Я»ѓЯ«▓Я««Я»Ї ╬И = sinРѕњ1 x Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, sinРѕњ1 (sin ╬И) = ╬И.
Я«фЯ«БЯ»ЇЯ«фЯ»ЂРѕњII
(i) x Рѕѕ [Рѕњ1,1] Я«јЯ«ЕЯ«┐Я«▓Я»Ї, sin(sinРѕњ1 x) = x
(ii) x Рѕѕ [Рѕњ1,1] Я«јЯ«ЕЯ«┐Я«▓Я»Ї, cos(cosРѕњ1 x) = x
(iii) x Рѕѕ РёЮ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, tan(tanРѕњ1 x) = x
(iv) xРѕѕ РёЮ \(Рѕњ1,1) Я«јЯ«ЕЯ«┐Я«▓Я»Ї, cosec(cosecРѕњ1 x) = x
(v) x Рѕѕ РёЮ \(Рѕњ1,1) Я«јЯ«ЕЯ«┐Я«▓Я»Ї, sec(secРѕњ1 x) = x
(vi) x Рѕѕ РёЮ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, cot(cotРѕњ1 x) = x
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї
(i) x Рѕѕ [Рѕњ1,1] Я«јЯ«ЕЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, sinРѕњ1 x Я«еЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
sinРѕњ1 x = ╬И Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є, Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ ╬И Рѕѕ [Рѕњ¤ђ/2, ¤ђ/2] Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї sin ╬И = x Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, sin ╬И = x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ sin(sinРѕњ1 x) = x Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«ЄЯ«цЯ»ЄЯ«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я«▒Я»ЇЯ«▒ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
(i) Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»ЇЯ«џЯ«ЙЯ«░Я»ЇЯ«фЯ»Ђ y = f(x), РѕњЯ«ЋЯ»ЇЯ«ЋЯ»Ђ, fРѕњЯ«ЕЯ»Ї Я«хЯ»ђЯ«џЯ»ЇЯ«џЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ xРѕњЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї f(fРѕњ1 (x)) = x Я«єЯ«ЋЯ»ЂЯ««Я»Ї. fРѕњ1 (x)РѕњЯ«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЄЯ«цЯ«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї. f(gРѕњ1(x)) Я«јЯ«ЕЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ gРѕњ1(x) = sinРѕњ1x Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ cosРѕњ1x Я«ЁЯ«цЯ»ЇЯ«цЯ«ЋЯ»ѕЯ«» Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ѕ Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ, Я«еЯ»ЄЯ«░Я»ЇЯ««Я«ЙЯ«▒Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»ѕ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»ѕ Я«хЯ«░Я»ѕЯ«хЯ«цЯ»Ђ Я«ЁЯ«хЯ«џЯ«┐Я«»Я««Я«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЅЯ«цЯ«ЙЯ«░Я«БЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ cot(sinРѕњ1x) РѕњЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»ѕ, sinРѕњ1x РѕњЯ«љ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«хЯ«░Я»ѕЯ«»Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ЂЯ««Я»Ї, fРѕњ1 (f(x)) Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѕЯ«»Я«ЙЯ«│Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЋЯ«хЯ«ЕЯ««Я»Ї Я«џЯ»єЯ«▓Я»ЂЯ«цЯ»ЇЯ«ц Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
(ii) f Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«єЯ«▒Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, fРѕњ1[f(x)] РѕњЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЂЯ«цЯ«▓Я»Ї.
(Я«Ё) x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ f РѕњЯ«ЕЯ»Ї Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї fРѕњ1[f(x)] = x Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(Я«є) x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ f РѕњЯ«ЕЯ»Ї Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«▓Я»ЇЯ«▓Я»ѕЯ«»Я»єЯ«ЕЯ«┐Я«▓Я»Ї f РѕњЯ«ЕЯ»Ї Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї f(x) = f(x1) Я«јЯ«ЕЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ x1РѕњЯ«љ Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«» Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«ЕЯ«┐, fРѕњ1[f(x)] = x1.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ,
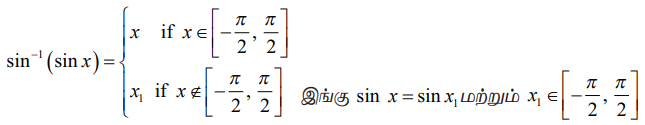
Я«фЯ«БЯ»ЇЯ«фЯ»ЂРѕњIII (Я«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я»Ї Я«еЯ»ЄЯ«░Я»ЇЯ««Я«ЙЯ«▒Я»Ђ Я««Я»ЂЯ«▒Я»ЇЯ«▒Я»іЯ«░Я»ЂЯ««Я»ѕЯ«ЋЯ«│Я»Ї)
(i) x Рѕѕ РёЮ \(Рѕњ1,1) Я«јЯ«ЕЯ«┐Я«▓Я»Ї, sinРѕњ1(1/x) = cosecРѕњ1x
(ii) x Рѕѕ РёЮ \(Рѕњ1, 1) Я«јЯ«ЕЯ«┐Я«▓Я»Ї, cosРѕњ1(1/x) = secxРѕњ1x
(iii) 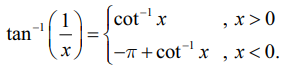
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї
(i) x Рѕѕ РёЮ \(Рѕњ1,1) Я«јЯ«ЕЯ«┐Я«▓Я»Ї, 1/x Рѕѕ [Рѕњ1,1] Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x РЅа 0Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, sinРѕњ1(1/x) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«еЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ.
sinРѕњ1(1/x) = ╬И Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є, Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«»Я«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐ ╬И Рѕѕ [Рѕњ¤ђ/2, ¤ђ/2]\{0} Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї sin ╬И = 1/x.
Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, cosec ╬И = x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ ╬И = cosecРѕњ1x Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«ЄЯ«ЕЯ«┐, sinРѕњ1(1/x) = ╬И = cosecРѕњ1 x Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, sinРѕњ1(1/x) = cosecРѕњ1 x , x Рѕѕ РёЮ \(Рѕњ1,1) Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«цЯ»Є Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я«▒Я»ЇЯ«▒ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«фЯ«БЯ»ЇЯ«фЯ»ЂРѕњIV (Я«фЯ«┐Я«░Я«цЯ«┐Я«фЯ«▓Я«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«▒Я»ЇЯ«▒Я»іЯ«░Я»ЂЯ««Я»ѕЯ«ЋЯ«│Я»Ї)
(i) x Рѕѕ [Рѕњ1, 1] Я«јЯ«ЕЯ«┐Я«▓Я»Ї, sinРѕњ1(Рѕњx) = Рѕњ sinРѕњ1 x.
(ii) x Рѕѕ РёЮ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, tanРѕњ1(Рѕњx) = РђЊ tanРѕњ1x .
(iii) |x| РЅЦ 1Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ x Рѕѕ РёЮ \(Рѕњ1, 1) Я«јЯ«ЕЯ«┐Я«▓Я»Ї, cosecРѕњ1(Рѕњx) = Рѕњ cosecРѕњ1x
(iv) x Рѕѕ [Рѕњ1, 1] Я«јЯ«ЕЯ«┐Я«▓Я»Ї, cosРѕњ1(Рѕњx) = ¤ђ РђЊ cosРѕњ1x .
(v) |x| РЅЦ 1 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ x Рѕѕ РёЮ \(Рѕњ1, 1) Я«јЯ«ЕЯ«┐Я«▓Я»Ї, secРѕњ1(Рѕњx) = ¤ђ РђЊ secРѕњ1x .
(vi) x Рѕѕ РёЮ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, cotРѕњ1(Рѕњx) = ¤ђ РђЊ cotРѕњ1x .
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї
(i) x Рѕѕ [Рѕњ1, 1] Я«јЯ«ЕЯ«┐Я«▓Я»Ї, РђЊx Рѕѕ [Рѕњ1, 1] Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, sinРѕњ1(Рѕњx) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«еЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ
sinРѕњ1(Рѕњx) = ╬И Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є ╬И Рѕѕ [Рѕњ¤ђ/2, ¤ђ/2] Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї sin ╬И = Рѕњ x Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, sin ╬И = Рѕњx РѕњЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ x = Рѕњsin ╬И = sin(Рѕњ╬И) Я«јЯ«Е Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
x = sin(Рѕњ╬И) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ, sinРѕњ1 x = Рѕњ ╬И Я«јЯ«Е Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ ╬И = РѕњsinРѕњ1x Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, sinРѕњ1(Рѕњx) = РѕњsinРѕњ1x Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(iv) x Рѕѕ [Рѕњ1, 1] Я«јЯ«ЕЯ«┐Я«▓Я»Ї, РђЊx Рѕѕ [Рѕњ1, 1] Я«јЯ«Е Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, cosРѕњ1(Рѕњx) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«еЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ.
cosРѕњ1(Рѕњx) = ╬И Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є ╬И Рѕѕ [0, ¤ђ] Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї cos ╬И = Рѕњx Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, cos ╬И = Рѕњx Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї x = Рѕњcos ╬И = cos(¤ђ Рѕњ ╬И) Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, ¤ђ Рѕњ ╬И = cosРѕњ1x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї ╬И = ¤ђ Рѕњ cosРѕњ1x Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є cosРѕњ1(Рѕњx) = ¤ђ Рѕњ cosРѕњ1x Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«цЯ»Є Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЈЯ«ЕЯ»ѕЯ«» Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
(i) Я«њЯ«ЕЯ»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«џЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«еЯ»ЄЯ«░Я»ЇЯ««Я«ЙЯ«▒Я»Ђ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ««Я»Ї Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«џЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ, [Рѕњ¤ђ/2, ¤ђ/2] Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«џЯ»ѕЯ«ЕЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«џЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї y = sinРѕњ1x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЊЯ«░Я»Ї Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«џЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
(ii) Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«џЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«еЯ»ЄЯ«░Я»ЇЯ««Я«ЙЯ«▒Я»Ђ Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«џЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЙЯ«ЋЯ»ЂЯ««Я«Й? Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«ЕЯ«ЙЯ«хЯ«┐Я«ЕЯ»ѕ Я«ЁЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ««Я«▒Я»ЇЯ«▒ Я«хЯ«┐Я«ЕЯ«Й Я«јЯ«Е Я«фЯ»ЂЯ«▒Я«ЋЯ»ЇЯ«ЋЯ«БЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«хЯ«┐Я«ЪЯ«▓Я«ЙЯ««Я»Ї. Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ѕЯ«цЯ»Ї Я«цЯ«хЯ«┐Я«░ Я«хЯ»ЄЯ«▒Я»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЊЯ«░Я»Ї Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«џЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«цЯ»Ђ. cosРѕњ1x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї secРѕњ1x Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«џЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«ЋЯ«хЯ«ЕЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
Я«фЯ«БЯ»ЇЯ«фЯ»ЂРѕњV (Я«цЯ»ЂЯ«БЯ»ѕ Я«еЯ»ЄЯ«░Я»ЇЯ««Я«ЙЯ«▒Я»ЂЯ«џЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«▒Я»ЇЯ«▒Я»іЯ«░Я»ЂЯ««Я»ѕЯ«ЋЯ«│Я»Ї )
(i) sinРѕњ1x + cosРѕњ1 = ¤ђ/2, x Рѕѕ [Рѕњ1, 1].
(ii) tanРѕњ1x + cotРѕњ1x = ¤ђ/2, x Рѕѕ РёЮ .
(iii) cosecРѕњ1x + secРѕњ1 x = ¤ђ/2, x Рѕѕ РёЮ \(Рѕњ1, 1) Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ |x| РЅЦ 1.
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї
(i) Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, x Рѕѕ [Рѕњ1, 1]. sinРѕњ1(x) = ╬И Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є ╬И Рѕѕ [Рѕњ¤ђ/2, ¤ђ/2] Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї sin ╬И = x Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Рѕњ¤ђ/2 РЅц ╬И РЅц ¤ђ/2 РЄћ 0 РЅц ¤ђ/2 РђЊ ╬И РЅц ¤ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«хЯ«ЕЯ«┐Я«ЋЯ»ЇЯ«Ћ.
Я«јЯ«ЕЯ«хЯ»Є, cos(¤ђ/2 РђЊ ╬И) = sin ╬И = x , Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ cosРѕњ1 x = ¤ђ/2 РђЊ ╬И = ¤ђ/2 РђЊ sinРѕњ1x Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, cosРѕњ1x + sinРѕњ1x = ¤ђ/2 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(ii) cotРѕњ1(x) = ╬И Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є, cot ╬И = x, 0 < ╬И < ¤ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x Рѕѕ РёЮ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«ЕЯ«┐, tan(¤ђ/2 РђЊ ╬И) = cot ╬И = x Я«єЯ«ЋЯ»ЂЯ««Я»Ї. РђдРђдРђдРђд(1)
Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, x Рѕѕ РёЮ РѕњЯ«ЋЯ»ЇЯ«ЋЯ»Ђ tan(tanРѕњ1 x) = x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (1)РѕњЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ tan(tanРѕњ1 x) = tan(¤ђ/2 РђЊ ╬И) Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, tan(tanРѕњ1x) = tan(¤ђ/2 РђЊ cotРѕњ1x) Я«єЯ«ЋЯ»ЂЯ««Я»Ї. РђдРђдРђдРђд(2)
0 < cotРѕњ1x < ¤ђ РѕњЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Рѕњ¤ђ/2 < ¤ђ/2 РђЊ cotРѕњ1x < ¤ђ/2 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«хЯ«ЕЯ«┐Я«ЋЯ»ЇЯ«Ћ
Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, (2) Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ tanРѕњ1x = ¤ђ/2 РђЊ cotРѕњ1x Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, tanРѕњ1 x + cotРѕњ1x = ¤ђ/2, x Рѕѕ РёЮ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«цЯ»Є Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ, (iii) Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«фЯ«БЯ»ЇЯ«фЯ»Ђ VI
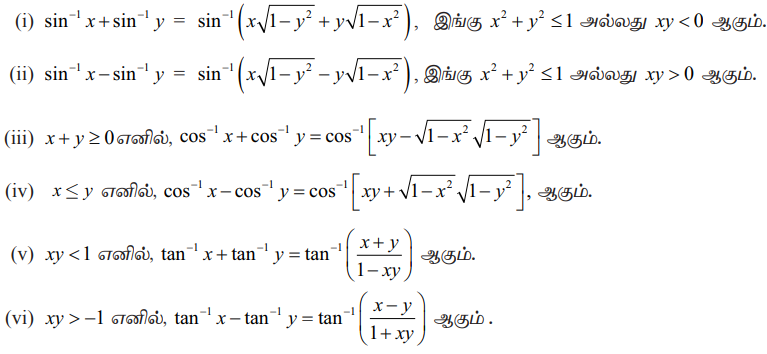
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї
(i) A = sinРѕњ1x. Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є, x = sin A; A Рѕѕ [Рѕњ¤ђ/2, ¤ђ/2]; |x| РЅц 1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї cos A Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я«┐Я«ЋЯ»ѕЯ«»Я»єЯ«БЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. B =sinРѕњ1 y. Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є, y = sin B ; B Рѕѕ [Рѕњ¤ђ/2, ¤ђ/2]; |y| РЅц 1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї cos B Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«ЕЯ«┐, cos A = +Рѕџ[1 Рѕњ sin2A ] = Рѕџ[1 Рѕњ x2] Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї cos B = +Рѕџ[1Рѕњ sin2 B] = Рѕџ[1 Рѕњ y2] Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, sin(A + B) = sin A cos B + cos Asin B
= xРѕџ[1 Рѕњ y2] + yРѕџ[1Рѕњx2], Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ |x| РЅц 1; |y| РЅц 1 Я«јЯ«ЕЯ«хЯ»Є, x2 + y2 РЅц 1
Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, A + B = sinРѕњ1(xРѕџ[1 Рѕњ y2] + yРѕџ[1 Рѕњ x2])
Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, sinРѕњ1x + sinРѕњ1y = sinРѕњ1(xРѕџ[1 Рѕњ y2] + yРѕџ[1 Рѕњ x2]), Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ x2 + y2 РЅц 1 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ xy < 0.
Я«ЄЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»ІЯ«▓Я«хЯ»Є Я«ЈЯ«ЕЯ»ѕЯ«» Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«фЯ«БЯ»ЇЯ«фЯ»ЂРѕњVII
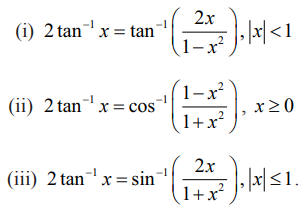
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї
(i) Я«фЯ«БЯ»ЇЯ«фЯ»ЂРѕњVI (v) РѕњЯ«▓Я»Ї, y = x Я«јЯ«Е Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї, Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕ Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї,
2 tanРѕњ1 x = tanРѕњ1 (2x /[1Рѕњ x2]), |x| < 1 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(ii) ╬И = 2 tanРѕњ1x Я«јЯ«ЕЯ«хЯ»Є, tan ╬И/2 = x.
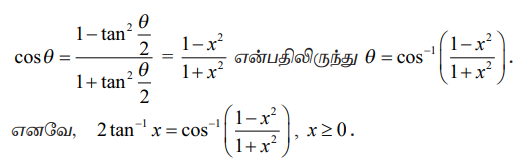
Я«ЄЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»ІЯ«▓Я«хЯ»Є Я«ЈЯ«ЕЯ»ѕЯ«» Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«фЯ«БЯ»ЇЯ«фЯ»ЂРѕњVIII
(i) |x| РЅц 1/Рѕџ2 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ РђЊ1/Рѕџ2 РЅц x РЅц 1/Рѕџ2 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, 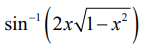 = 2 sinРѕњ1 x
= 2 sinРѕњ1 x
(ii) 1/Рѕџ2 РЅц x РЅц 1 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, 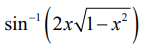 = 2 cosРѕњ1 x
= 2 cosРѕњ1 x
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї
(i) x = sin ╬И. Я«јЯ«ЕЯ«хЯ»Є x РЅц1
Я«ЄЯ«ЕЯ«┐, 2x /Рѕџ[1Рѕњ x2] = 2 sin ╬И cos ╬И = sin 2╬И
Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, 2╬И =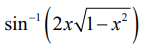 . Я«јЯ«ЕЯ«хЯ»Є,
. Я«јЯ«ЕЯ«хЯ»Є, 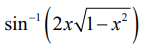 = 2 sinРѕњ1 x.
= 2 sinРѕњ1 x.
(ii) x = cos ╬И.
Я«ЄЯ«ЕЯ«┐, 2x /Рѕџ[1Рѕњ x2] = 2 cos ╬И sin ╬И = sin 2╬И
Я«јЯ«ЕЯ«хЯ»Є, 2╬И = 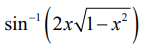 . Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї,
. Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, 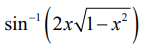 = 2 cosРѕњ1 x.
= 2 cosРѕњ1 x.
Я«фЯ«БЯ»ЇЯ«фЯ»ЂРѕњIX
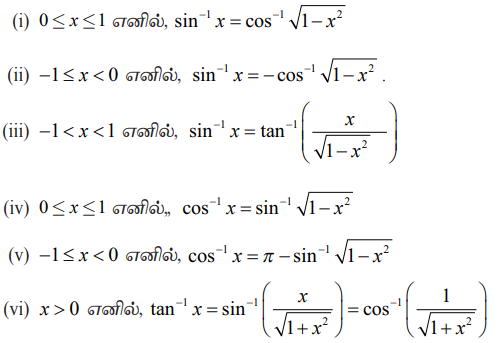
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї
(i) sinРѕњ1x = ╬И Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є, sin ╬И = x, 0 РЅц x РЅц1 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї 0 РЅц ╬И РЅц ¤ђ/2 Я«јЯ«Е Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«ЄЯ«ЕЯ«┐, cos ╬И = Рѕџ[1Рѕњ x2] Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ cosРѕњ1Рѕџ[1Рѕњ x2] = ╬И = sinРѕњ1x .
Я«јЯ«ЕЯ«хЯ»Є, sinРѕњ1x = cosРѕњ1Рѕџ[1Рѕњ x2] , 0 РЅц x РЅц 1
(ii) Рѕњ1 РЅц x РЅц 0 Я«јЯ«ЕЯ»ЇЯ«Ћ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї sinРѕњ1x = ╬И. Я«јЯ«ЕЯ«хЯ»Є Рѕњ¤ђ/2 РЅц ╬И < 0
Я«ЁЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї, sin ╬И = x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї cos (Рѕњ╬И) = Рѕџ[1Рѕњ x2] (Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї cos ╬И > 0 )
Я«јЯ«ЕЯ«хЯ»Є, cosРѕњ1Рѕџ[1Рѕњ x2] = Рѕњ╬И = Рѕњ sinРѕњ1x. Я«јЯ«ЕЯ«хЯ»Є sinРѕњ1 x = РѕњcosРѕњ1 Рѕџ[1Рѕњ x2].
Я«ЄЯ«цЯ»Є Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЈЯ«ЕЯ»ѕЯ«» Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«фЯ«БЯ»ЇЯ«фЯ»ЂРѕњX
(i) 3 sinРѕњ1x = sinРѕњ1(3x Рѕњ 4x3), x = Рѕѕ [Рѕњ1/2, 1/2].
(ii) 3 cosРѕњ1x = cosРѕњ1(4x3 Рѕњ 3x), x = Рѕѕ [1/2, 1].
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї
x = sin ╬И Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, ╬И = sinРѕњ1 x.
Я«ЄЯ«ЕЯ«┐, 3x Рѕњ 4x3 = 3 sin ╬И Рѕњ 4 sin3 ╬И = sin 3 ╬И
Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, sinРѕњ1(3x Рѕњ 4x3) = 3╬И = 3sinРѕњ1 x.
Я«ЄЯ«цЯ»Є Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«цЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«░Я»ѕ
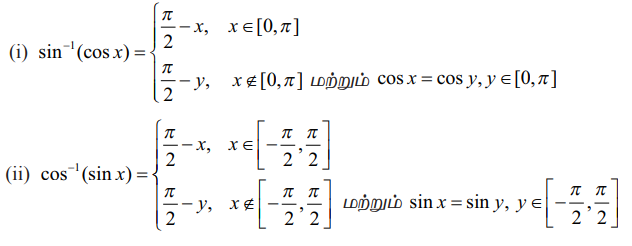
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.16
¤ђ/2 РЅц sinРѕњ1 x + 2cosРѕњ1 x РЅц 3¤ђ/2 Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
sinРѕњ1 x + 2cosРѕњ1 x = sinРѕњ1 x + cosРѕњ1 x + cosРѕњ1 x = ¤ђ/2 + cosРѕњ1 x
0 РЅц cosРѕњ1 x РЅц ¤ђ Я«јЯ«ЕЯ«хЯ»Є, ¤ђ/2 + 0 РЅц cosРѕњ1 x + ¤ђ/2 РЅц ¤ђ + ¤ђ/2 .
Я«јЯ«ЕЯ«хЯ»Є, ¤ђ/2 РЅц sinРѕњ1 x + 2cosРѕњ1 x РЅц 3¤ђ/2 .
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.17


Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.22
cosРѕњ1x + cosРѕњ1y + cosРѕњ1 z = ¤ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 0 < x, y, z < 1, Я«јЯ«ЕЯ«┐Я«▓Я»Ї
x2 + y2 + z2 + 2xyz = 1 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«┐.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
cosРѕњ1x = ╬▒ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї cosРѕњ1y = ╬▓ Я«јЯ«ЕЯ»ЇЯ«Ћ
Я«јЯ«ЕЯ«хЯ»Є, x = cos ╬▒ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y = cos ╬▓ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
cosРѕњ1x + cosРѕњ1y + cosРѕњ1 z = ¤ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ ╬▒ + ╬▓ = ¤ђ Рѕњ cosРѕњ1 z. РђдРђд..(1)
Я«ЄЯ«ЕЯ«┐, cos(╬▒ + ╬▓) = cos╬▒ cos ╬▓ РђЊ sin ╬▒ sin ╬▓ = xy Рѕњ Рѕџ[1Рѕњ x2] Рѕџ[1 Рѕњ y2].
(1)РѕњЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ cos(¤ђ Рѕњ cosРѕњ1z) = xy Рѕњ Рѕџ[1 Рѕњ x2] Рѕџ[1 Рѕњ y2] Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Рѕњcos(cosРѕњ1 z) = xy Рѕњ Рѕџ[1 Рѕњ x2] Рѕџ[1Рѕњy2].
Я«јЯ«ЕЯ«хЯ»Є, Рѕњz = xy Рѕњ Рѕџ[1Рѕњ x2] Рѕџ[1РђЊ ЛЃ2], Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Рѕњxy Рѕњ z = Рѕњ Рѕџ[1 Рѕњ x2] Рѕџ[1 Рѕњ y2]
Я«ЄЯ«░Я»ЂЯ«фЯ»ЂЯ«▒Я««Я»ЂЯ««Я»Ї Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«џЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ x2 + y2 + z2 + 2xyz = 1 Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.23
dРѕњЯ«љ Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ a1, a2, a3, Рђд an Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
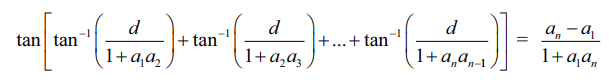 Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»Ђ.
Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»Ђ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
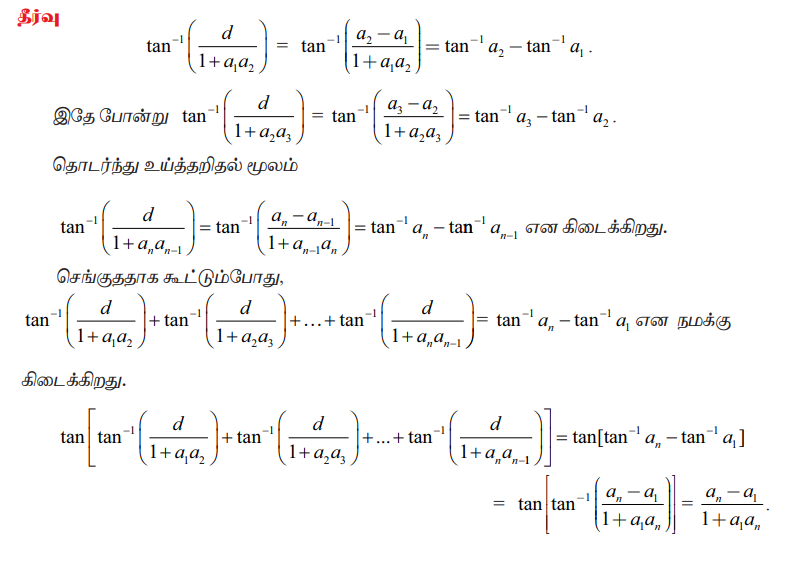
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.24
Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ tanРѕњ1 [(1Рѕњ x)/( 1 + x)] = 1/2 tanРѕњ1 x, Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ x > 0.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
tanРѕњ1 [(1Рѕњ x)/( 1 + x)] = 1/2 tanРѕњ1 x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ tanРѕњ11Рѕњ tanРѕњ1 x =1/2 tanРѕњ1 x.
Я«јЯ«ЕЯ«хЯ»Є, ¤ђ/4 = 3/2 tanРѕњ1 x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«»Я»Є Я«џЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐ tanРѕњ1 x = ¤ђ/6 Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЂЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, x = tan ¤ђ/6 = 1/Рѕџ3.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.25
Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ sinРѕњ1 x > cosРѕњ1 x
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
sinРѕњ1 x > cosРѕњ1 x Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
Я«ЄЯ«░Я»ЂЯ«фЯ»ЂЯ«▒Я««Я»ЂЯ««Я»Ї sinРѕњ1 x, РѕњЯ«љ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«Ъ
sinРѕњ1 x + sinРѕњ1 x > cosРѕњ1 x + sinРѕњ1 x, Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«џЯ»ЂЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐ 2sinРѕњ1 x > ¤ђ/2 .
[Рѕњ¤ђ/2, ¤ђ/2] Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї Я«џЯ»ѕЯ«ЕЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЈЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї, x > sin ¤ђ/4 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ x > 1/Рѕџ2 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«БЯ««Я«ЙЯ«Е Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐ (1/Рѕџ2 , 1] Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.26
cot(sinРѕњ1 x) = Рѕџ[1 Рѕњ x2] / x , Рѕњ1 РЅц x РЅц 1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x РЅа 0 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«┐.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
sinРѕњ1 x = ╬И . Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є, x = sin ╬И Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x РЅа 0, ╬И Рѕѕ [Рѕњ¤ђ/2, 0) Рѕф (0, ¤ђ/2] Я«јЯ«Е Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«Ћ Я«фЯ»єЯ«▒Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ,
cos ╬И РЅЦ 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї cos ╬И = Рѕџ[1Рѕњsin2╬И] = Рѕџ[1 Рѕњ x2].
Я«јЯ«ЕЯ«хЯ»Є, cot(sinРѕњ1 x) = cot ╬И = Рѕџ[1 Рѕњ x2] / x , |x| < 1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x РЅа 0.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.27
6x2 < 1 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, tanРѕњ1 2x + tanРѕњ1 3x = ¤ђ/4 , Я«љ Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ,
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
6x2 < 1 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, tanРѕњ1 2x + tanРѕњ1 3x = tanРѕњ1[(2x + 3x) / (1 Рѕњ 6x2)].
tanРѕњ1[(5x)/ (1 Рѕњ 6x2)] = ¤ђ/4, Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї (5x)/(1 Рѕњ 6x2) = tan (¤ђ/4) = 1
Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, 1 Рѕњ 6x2 = 5x, Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 6x2 + 5x Рѕњ 1= 0
Я«єЯ«ЋЯ«хЯ»Є, x = 1/6 , Рѕњ1
x = Рѕњ1 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«ЄЯ«ЪЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я»єЯ«БЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«▓Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Я««Я«┐Я«ЋЯ»ѕЯ«»Я»єЯ«БЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«цЯ«░Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«ЋЯ«хЯ«ЕЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, x = Рѕњ1 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»ђЯ«░Я»ЇЯ«хЯ«ЙЯ«ЋЯ«ЙЯ«цЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є, x = 1/6 Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.28
Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ 
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.29
Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ 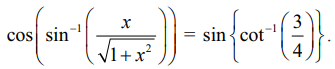
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
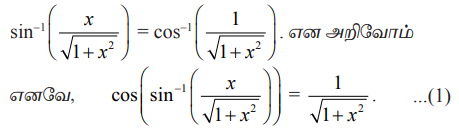
cotРѕњ1 (3/4) = ╬И. Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«░Я»Ї cot ╬И = ┬Й Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ╬И Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї.
Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ, Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»єЯ«▒Я»ЂЯ«хЯ«цЯ»Ђ
sin {cot Рѕњ1 (3/4)} = sin ╬И = 4/5 РђдРђдРђдРђдРђдРђд..(2)
(1) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (2)РѕњЯ«љ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ
1/Рѕџ(1 + x2) = 4/5 , Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Рѕџ[1 + x2 ] = 5/4 Я«јЯ«ЕЯ«хЯ»Є, x = ┬▒3/4.