கோடான்ஜெண்ட் சார்பு மற்றும் நேர்மாறு கோடான்ஜெண்ட் சார்பு (The Cotangent Function and the Inverse Cotangent Function)

கோடான்ஜெண்ட் சார்பு மற்றும் நேர்மாறு கோடான்ஜெண்ட் சார்பு (The Cotangent Function and the Inverse Cotangent Function)

கோடான்ஜெண்ட் சார்பு என்பது cot x = 1/tan x ஆகும். tan x = 0 அல்லது x = nπ, n ∈ ℤ எனும் மதிப்புகளைத் தவிர x −ன் ஏனைய மெய்யெண் மதிப்புகளுக்கு கோடான்ஜெண்ட் சார்பு வரையறுக்கப்படுகிறது. எனவே, கோடான்ஜெண்ட் சார்பின் சார்பகமானது ℝ\{ nπ : n ∈ ℤ } மற்றும் அதன் வீச்சகம் (−∞, ∞) ஆகும். tan x போன்று கோடான்ஜெண்ட் சார்பும் ஓர் ஒற்றைச் சார்பாகவும் மற்றும் அதன் காலம் π ஆகவும் உள்ளது.

1. கோடான்ஜெண்ட் சார்பின் வரைபடம் (The graph of the cotangent function) 

கோடான்ஜெண்ட் சார்பு (0, 2π)\{ π } எனும் கணத்தில் தொடர்ச்சியாக இருக்கிறது. (0, 2π)\{ π }.−ல் முதலில் கோடான்ஜெண்ட் சார்பின் வரைபடத்தை வரைவோம். முதல் மற்றும் மூன்றாம் காற்பகுதியில் கோடான்ஜெண்ட் மிகையெண் மதிப்புகளை மட்டுமே பெறுகிறது. இரண்டாவது மற்றும் நான்காவது காற்பகுதிகளில் குறையெண் மதிப்புகளை மட்டுமே பெறுகிறது. கோடான்ஜெண்ட் சார்பிற்கு மீப்பெரும்மோ அல்லது மீச்சிறுமமோ இல்லை. x ∈ (0, π/2] எனும்போது கோடான்ஜெஸ்ட் சார்பு, ∞ −லிருந்து 0 −க்கு இறங்குகிறது; . x ∈  [π/2, π) எனும்போது 0 −லிருந்து −∞ −க்கு இறங்குகிறது; x ∈  (π/2, 3π/2] எனும்போது −∞ லிருந்து 0 வரை இறங்குகிறது; x ∈ [3π/2, 2π) எனும்போது, 0−லிருந்து −∞ வரை இறங்குகிறது

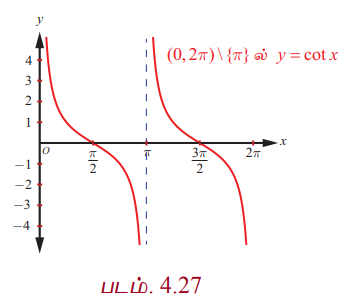
y = cot x , x ∈ (0, 2π)\{ π } −க்கான வரைபடம் படம் 4.27−ல் காண்பிக்கப்பட்டுள்ளது. 

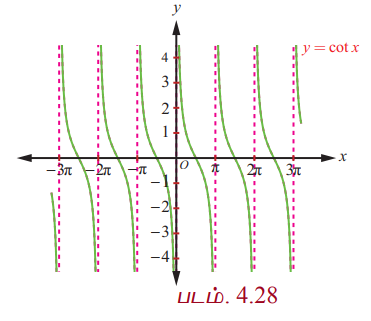
(0, 2π)\{ π }−ல் அமைந்த y = cot x ன் வரைபடம் போல (2π, 4π)\{3π} , (4π, 6π)\{5π}, … , மற்றும் …, (−4π, −2π)\{−3π}, (−2π, 0)\{−π}. ஆகிய இடைவெளிகளிலும் y = cot x ன் வரைப்படம் திரும்ப, திரும்ப அமைகிறது. ℝ\{ nπ : n ∈ ℤ } −ஐ சார்பகமாகக் கொண்ட கோடான்ஜெண்ட் சார்பின் முழு வரைபடமும் படம் 4.28−ல் காண்பிக்கப்பட்டுள்ளது.

2. நேர்மாறு கோடான்ஜெண்ட் சார்பு (Inverse cotangent function)

கோடான்ஜெண்ட் சார்பு அதன் முழுசார்பகத்தில் ℝ\{ nπ : n ∈ ℤ } ஒன்றுக்கொன்று சார்பு அல்ல. ஆயினும் கட்டுபடுத்தப்பட சார்பகமான (0, π)−ல், cot : (0, π) → (−∞, ∞) ஆனது இருபுறச் சார்பாகும். எனவே, (−∞, ∞) சார்பகமாகவும், (0, π) வீச்சாகவும் கொண்டு நேர்மாறு கோடான்செண்ட் சார்பை வரையறுப்போம்.

வரையறை 4.8

நேர்மாறு கோடான்ஜெண்ட் சார்பான cot−1 : (−∞, ∞) → (0, π) என்பது cot−1  (x) = y என வரையறுக்க தேவையானதும் மற்றும் போதுமானதுமான நிபந்தனைகள்  y ∈ (0, π) மற்றும் cot y = x ஆகும்.

3. நேர்மாறு கோடான்ஜெண்ட் சார்பின் வரைபடம் (Graph of the inverse cotangent function)

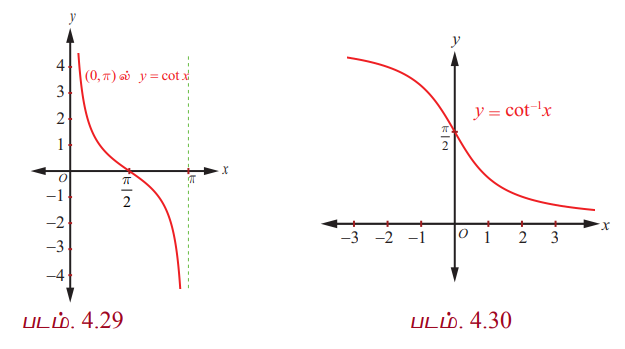
நேர்மாறு கோடான்ஜெண்ட் சார்பான y = cot−1 x என்பது ℝ −ஐ சார்பகமாகவும் மற்றும் (0, π) −ஐ வீச்சாகவும் கொண்ட சார்பாகும். அதாவது cot−1 x : (−∞, ∞) → (0, π) ஆகும். 

படம் 4.29 மற்றும் படம். 4.30 ஆகியவற்றில் வரைபடங்கள் முறையே முதன்மை சார்பகத்தில் கோடான்ஜெண்ட் சார்பின் வரைபடம் மற்றும் நேர்மாறு கோடான்ஜெண்ட் சார்பின் வரைபடம் அதற்குரிய சார்பகத்திலும் கொடுக்கப்பட்டுள்ளன.