எடுத்துக்காட்டு கணக்குகள்: நேர்மாறு முக்கோணவியல் சார்புகளின் முதன்மை மதிப்பு

எடுத்துக்காட்டு 4.1

ஆரையன் மற்றும் பாகைகளில் sin−1(−1/2) −ன் முதன்மை மதிப்பைக் காண்க.

தீர்வு

sin−1(−1/2) = y என்க. எனவே, sin y = −1/2 ஆகும்.

sin−1x  −ன் முதன்மை மதிப்புகளின் வீச்சகம் [−π/2, π/2] ஆகும். எனவே sin y = −1/2 என்றவாறு y ∈ [−π/2, π/2] ஐ கண்டறியவேண்டும். ஆகவே y = −π/6 எனக் கிடைக்கின்றது. எனவே sin−1(−1/2) −ன் முதன்மை மதிப்பு −π/6 ஆகும். அதன் ஒத்த மதிப்பு −30° ஆகும்.

எடுத்துக்காட்டு 4.2

sin−1 (2) −ன் முதன்மை மதிப்பு இருப்பின், அதனை கண்டறிக.

தீர்வு

y = sin−1x −ன் சார்பகம் [−1, 1] என்பதாலும் 2 ∉ [−1,1] என்பதாலும் sin−1(2) −க்கு முதன்மை மதிப்பு இல்லை.

எடுத்துக்காட்டு 4.3

முதன்மை மதிப்பைக்காண்க.

(i) sin−1 (1/ √2)

(ii) sin−1[sin(−π/3)]

(iii) sin−1[sin(5π/6)]

தீர்வு

sin−1 : [−1, 1] → [−π/2, π/2] என்பது sin−1 x = y என கொடுக்கப்படத் தேவையானதும் மற்றும் போதுமானதுமான நிபந்தனை x = sin y ஆகும். இங்கு −1 ≤  x  ≤ 1 மற்றும் −π/2 ≤ y  ≤ π/2. எனவே,

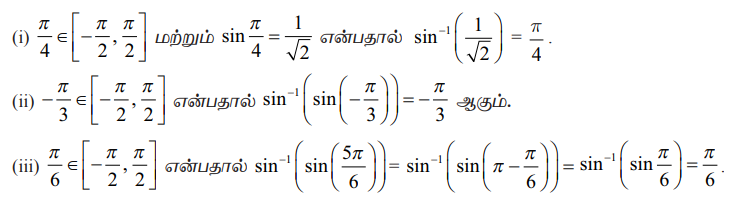
எடுத்துக்காட்டு 4.4

sin−1(2 − 3x2)−ன் சார்பகத்தைக் காண்க.

தீர்வு 

sin−1 (x) −ன் சார்பகம் [−1,1) ஆகும்.

எனவே −1 ≤ 2 − 3x2 ≤ 1. ஆகையால் −3 ≤ −3x2 ≤ −1.

−3 ≤ −3x2, எனும்போது x2 ≤ 1          …………..(1)

−3x2 ≤ −1, எனும்போது x2 ≥ 1/3          …………..(2)

சமன்பாடுகள்(1) மற்றும் (2), ஆகியவற்றிலிருந்து 1/3 ≤ x2 ≤ 1 எனக் கிடைக்கிறது. எனவே, 1/√3 ≤ |x| ≤ 1.

a ≤ |x| ≤ b என்பதிலிருந்து x ∈ [–b,−a] ∪ [a,b] என கிடைக்கும் என்பதால்,

எனவே, x ∈ [–1, −1/√3] ∪ [1/√3 , 1]

எடுத்துக்காட்டு 4.5

cos–l [√3/2] −ன் முதன்மை மதிப்பைக் காண்க .

தீர்வு

cos–l [√3/2] = y என்க. எனவே, cos y = √3/2 ஆகும்.

y = cos–l x  −ன் முதன்மை மதிப்பு வீச்சகம் [0, π] என நாம் அறிவோம். எனவே, cos y = √3/2 எனும்படி y மதிப்பு [0, π] −ல் காண வேண்டும். ஆனால், cos π/6 = √3/2 மற்றும் π/6 ∈ [0, π] என்பதால் y = π/6  ஆகும். எனவே, cos–l [√3/2] −ன் முதன்மை மதிப்பு π /6  ஆகும்.

எடுத்துக்காட்டு 4.6 

மதிப்பு காண்க

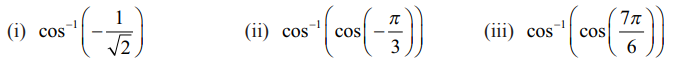
தீர்வு

cos–l : [−1,1] → [0, π] எனும் நேர்மாறு கொசைன் சார்பு வரையறையின்படி, cos–l x = y எனில், எனில் மட்டுமே cos y = x . இங்கு −1 ≤x ≤ 1 மற்றும் 0 ≤ y ≤  π ஆகையால்,

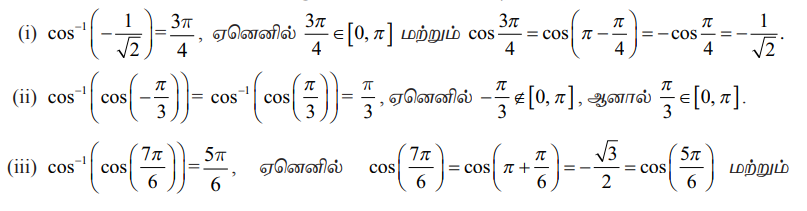
எடுத்துக்காட்டு 4.7

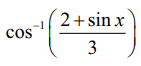−ன் சார்பகம் காண்க.

தீர்வு

y = cos–l x −ன் சார்பகம் −1 ≤ x ≤ 1 அதாவது |x| ≤ 1ஆகும்.

எனவே, −1 ≤  (2+sin x)/3 ≤ 1 என்பதை −3 ≤  2 + sin x ≤  3 எனலாம்.

எனவே, −5 ≤  sin x ≤  1 என்பதை சுருக்கி, −1 ≤  sin x ≤  1 எனப் பெறலாம்,

sin–l (l) ≤ x ≤ sin–l (1) அல்லது −π/2 ≤ x  ≤ π/2 எனப் பெறலாம்.         

ஆகையால் 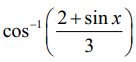 −ன் சார்பகம் [−π/2, π/2] ஆகும்.

எடுத்துக்காட்டு 4.8

முதன்மை மதிப்பு காண்க: tan–l (√3).

தீர்வு

tan–l (√3) = y என்க. எனவே, tan y = √3. ஆகையால்,  y =  π/3 ஏனெனில் π/3 ∈ [−π/2, π/2] எனவே, tan–l (√3) ன் முதன்மை மதிப்பு π/3 ஆகும்.

எடுத்துக்காட்டு 4.9

மதிப்பு காண்க 

(i) tan–l (−√3) 

(ii) tan–l[tan(3π/5)]

(iii) tan(tan–l (2019))

தீர்வு

(i) tan–l (−√3) = tan–l[tan(−π/3)] = −π/3 , ஏனெனில் −π/3 ∈ [−π/2, π/2].

(ii) tan–l[tan(3π/5)]

tan θ = tan(3π/5) எனுமாறு θ ∈ [−π/2, π/2]. ஐ நாம் கண்டறிய வேண்டும்.

தொடுகோட்டுச் சார்பின் காலம் π  என்பதால், tan(3π/5) = tan(3π/5 −π) = tan(−2π/5)  

எனவே, tan–l[tan(3π/5)] = tan–l[tan(−2π/5)]  = −2π/5 , ஏனெனில் −2π/5 ∈ [−π/2, π/2].

(iii) tan(tan–l x) = x, x ∈ ℝ என்பதால், tan(tan–l (2019)) = 2019 ஆகும்.

எடுத்துக்காட்டு 4.10

மதிப்பு காண்க tan–l(−1) + cos–l(1/2) + sin–l(−1/2).

தீர்வு

tan–l (−1) = y என்க. எனவே, tan y = −1 = − tan(π/4) = tan(−π/4). 

இங்கு −π/4 ∈ [−π/2, π/2] என்பது குறிப்பிடதக்கது. எனவே, tan–l (−1) = −π/4 .

இனி, cos–l (1/2) =  y எனில் cos y = 1/2 = cos π/3 .

π/3 ∈ [0, π] என்பதால் cos–l (1/2) = π/3

மேலும், sin–l(−1/2) = y எனில் sin y = −1/2 = sin(−π/6)

−π/6 ∈ [−π/2, π/2] என்பதால் sin–l(−1/2) = −π/6 .

எனவே , tan–l(−1) + cos–l(1/2) + sin–l(−1/2) =  −π/4 + π/3 − π/6 = − π/12 .

எடுத்துக்காட்டு 4.11

நிரூபி tan(sin–l x) =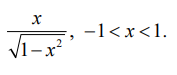

தீர்வு

x = 0 எனில், இருபுறமும் 0 ஆகும். 

0 < x < 1. என்க.

θ = sin–l x என்க. எனவே 0 < θ < π/2 ஆகும். தற்போது sin θ = x /1 என்பதால்,.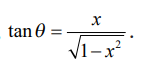

எனவே tan (sin–l x) =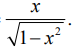

அடுத்தாக −1 < x < 0 என்க. எனவே, θ = sin–l x என்பதிலிருந்து −π/2 < θ < 0.

sin θ = x /1 என்பதால், tan θ =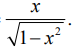

இம்முறையிலும் tan (sin–l x) = 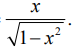என கிடைக்கின்றது.

சமன்பாடுகள் (1), (2) மற்றும் (3) ஆகியவற்றிலிருந்து tan (sin–l x) = 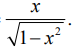  , −1 < x < 1 என நிறுவப்படுகின்றது.

எடுத்துக்காட்டு 4.12

முதன்மை மதிப்பு காண்க

(i) cosec−1 (−1)

(ii) sec−1 (−2)

தீர்வு

(i) cosec−1 (−1) = y என்க. எனவே, cosec y = −1

y = cosec−1 x −ன் முதன்மை மதிப்பிற்குரிய வீச்சகம் [−π/2, π/2]\{0} ஆகும். மேலும்,

cosec(−π/2) = −1 என்பதால், y = −π/2 என்றிருக்க வேண்டும். இங்கு −π/2 ∈ [−π/2, π/2]\{0}

என்பதை கவனிக்க.

எனவே, cosec−1 (−1) −ன் முதன்மை மதிப்பு −π/2 ஆகும்.

(ii) y=sec−1 (−2) என்க. எனவே, sec y = −2 .

y = sec−1  x −ன் முதன்மை மதிப்பிற்குரிய வீச்சகம் [0, π]\ { π/2} ஆகும்.

sec y = −2 என்றிருக்குமாறு [0, π] − { π/2} −ல் y−ஐ காணவேண்டும்.

ஆனால் sec y = −2 ⇒ cos y = −1/2

இனி, cos y = −1/2 = −cos π/3 = cos [π − π/3] = cos 2π/3 . எனவே, y = 2π/3.

2π/3 ∈ [0, π] \ { π/2} என்பதால், sec−1 (−2) −ன் முதன்மை மதிப்பு 2π/3 ஆகும்.

எடுத்துக்காட்டு 4.13

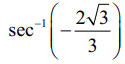ன் மதிப்பு காண்க.

தீர்வு

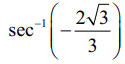= θ என்க. எனவே, sec θ = −2/√3 இங்கு θ ∈ [0, π] \ { π/2} ஆகும்.

எனவே, cos θ = −√3/2 ஆகும். இனி, cos 5π/6 = cos [π − π/6] = −cos [π/6] = −√3/2 ஆகும்.

எனவே, 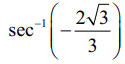 = 5π/6 ஆகும்.

எடுத்துக்காட்டு 4.14

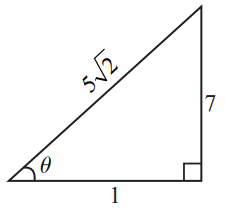
cot−1 (1/7) = θ , எனில், cos θ மதிப்பு காண்க.

தீர்வு

வரையறைப்படி cot−1  x ∈ (0, π).

எனவே, cot−1 (1/7) = θ என்பதிலிருந்து θ ∈ (0, π).ஆகும்.

ஆனால் cot−1 (1/7) = θ என்பது cot θ = 1/7 ஆகும். எனவே tan θ = 7 மற்றும் θ ஒரு குறுங்கோணம் ஆகும்.

tan θ = 7/1 என்பதை பயன்படுத்தி, செங்கோண முக்கோணம் ஒன்றை உருவாக்குக. பின்னர்

cos θ = 1 / 5√2 என நமக்கு கிடைக்கிறது.

எடுத்துக்காட்டு 4.15

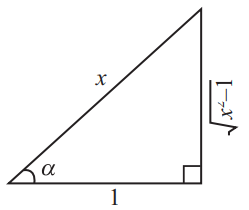
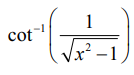= sec−1x, |x| > 1. எனக் காட்டுக

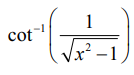= α என்க. எனவே, cot α =1/(√[x2 – 1])

மற்றும் α ஒரு குறுங்கோணம் ஆகும்.

கொடுக்கப்பட்ட விவரங்களைக் கொண்டு ஒரு செங்கோண முக்கோணம் உருவாக்குக. 

முக்கோணத்திலிருந்து, sec α = x/1 = x எனப் பெறலாம் . எனவே, α = sec−1 x ஆகும்.

எனவே 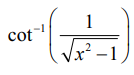= sec−1x, |x| > 1 ஆகும்.

எடுத்துக்காட்டு 4.16

π/2 ≤ sin−1 x + 2cos−1 x ≤ 3π/2 என நிறுவுக.

தீர்வு

sin−1 x + 2cos−1 x = sin−1 x + cos−1 x + cos−1 x = π/2 + cos−1 x

0 ≤ cos−1 x ≤ π எனவே, π/2 + 0 ≤ cos−1 x + π/2 ≤ π + π/2 .

எனவே, π/2  ≤ sin−1 x + 2cos−1 x ≤ 3π/2 .

எடுத்துக்காட்டு 4.17

எடுத்துக்காட்டு 4.22

cos−1x + cos−1y + cos−1 z = π மற்றும் 0 < x, y, z < 1, எனில் 

x2 + y2 + z2 + 2xyz = 1 எனக் காண்பி.

தீர்வு

cos−1x = α மற்றும் cos−1y = β என்க

எனவே, x = cos α மற்றும் y = cos β ஆகும்.

cos−1x + cos−1y + cos−1 z = π என்பதிலிருந்து α + β = π − cos−1 z.  ……..(1)

இனி, cos(α + β) = cosα cos β – sin α sin β = xy − √[1− x2] √[1 − y2].

(1)−லிருந்து cos(π − cos−1z) = xy − √[1 − x2] √[1 − y2] எனப் பெறலாம்.

−cos(cos−1 z) = xy − √[1 − x2] √[1−y2]. 

எனவே, −z = xy − √[1− x2] √[1– у2], என்பதிலிருந்து −xy − z = − √[1 − x2] √[1 − y2]

இருபுறமும் வர்க்கப்படுத்தி சுருக்க x2 + y2 + z2 + 2xyz = 1 எனப் பெறலாம்.

எடுத்துக்காட்டு 4.23

d−ஐ பொது வித்தியாசமாகக் கொண்டு a1, a2, a3, … an ஒரு கூட்டுத் தொடர் எனில்,

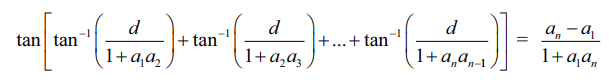  என நிறுவு.

தீர்வு

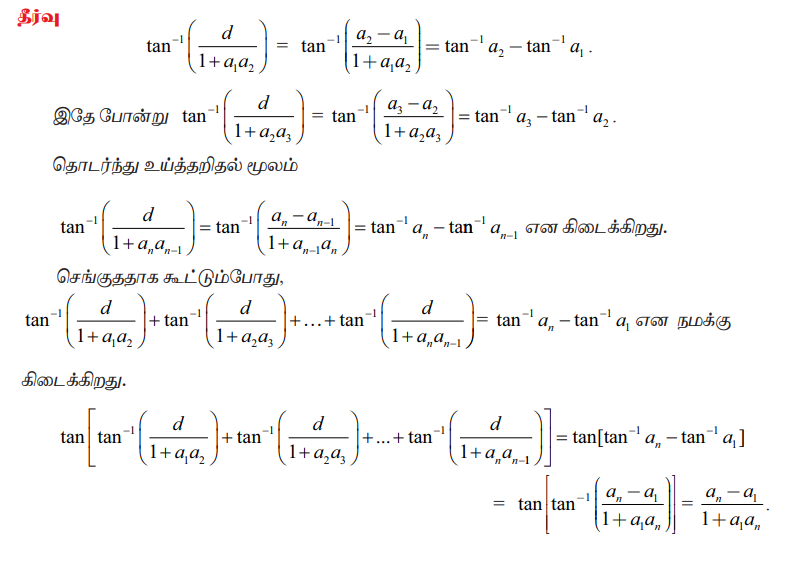
எடுத்துக்காட்டு 4.24

தீர்க்க tan−1 [(1− x)/( 1 + x)] = 1/2 tan−1 x, இங்கு x > 0.

தீர்வு

tan−1 [(1− x)/( 1 + x)] = 1/2 tan−1 x என்பதிலிருந்து tan−11− tan−1 x =1/2 tan−1 x.

எனவே, π/4 = 3/2 tan−1 x என்பதையே சுருக்கி tan−1 x = π/6 எனப் பெறுகிறோம்.

எனவே, x = tan π/6 = 1/√3.

எடுத்துக்காட்டு 4.25

தீர்க்க sin−1 x > cos−1 x

தீர்வு

sin−1 x > cos−1 x எனக் கொடுக்கப்பட்டுள்ளது.

இருபுறமும் sin−1 x, −ஐ கூட்ட

sin−1 x + sin−1 x > cos−1 x + sin−1 x, என்பது சுருங்கி 2sin−1 x > π/2 .

[−π/2, π/2] எனும் இடைவெளியில் சைன் சார்பு மதிப்பு ஏறும் என்பதால், x > sin π/4 அல்லது x > 1/√2 ஆகும்.

ஆகையால் தீர்வு கணமான இடைவெளி (1/√2 , 1] ஆகும்.

எடுத்துக்காட்டு 4.26

cot(sin−1 x) = √[1 − x2] / x , −1 ≤ x ≤ 1 மற்றும் x ≠ 0 எனக் காண்பி.

தீர்வு

sin−1 x = θ . என்க. எனவே, x = sin θ மற்றும் x ≠ 0, θ ∈ [−π/2, 0) ∪ (0, π/2] என கிடைக்க பெறுகிறது,

cos θ ≥ 0 மற்றும் cos θ = √[1−sin2θ]  = √[1 − x2].

எனவே, cot(sin−1 x) = cot θ = √[1 − x2] / x , |x| < 1 மற்றும் x  ≠  0. 

எடுத்துக்காட்டு 4.27

6x2 < 1 எனில், tan−1 2x + tan−1 3x = π/4 , ஐ தீர்க்க,

தீர்வு

6x2 < 1 எனில், tan−1 2x + tan−1 3x = tan−1[(2x + 3x) / (1 − 6x2)].

tan−1[(5x)/ (1 − 6x2)] = π/4, என்பதால் (5x)/(1 − 6x2) = tan (π/4) = 1

ஆகையால், 1 − 6x2 = 5x, என்பதிலிருந்து 6x2 + 5x − 1= 0

ஆகவே, x = 1/6 , −1

x = −1 என்பது சமன்பாட்டின் இடப்புறம் குறையெண் மதிப்பையும் மற்றும் வலப்புறம் மிகையெண் மதிப்பையும் தருகிறது என்பதை கவனிக்கவும். ஆகையால், x = −1 என்பது தீர்வாகாது. எனவே, x = 1/6 மட்டுமே சமன்பாட்டிற்குத் தீர்வாக அமையும்.

எடுத்துக்காட்டு 4.28

தீர்க்க

எடுத்துக்காட்டு 4.29

தீர்க்க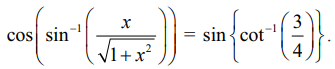

தீர்வு

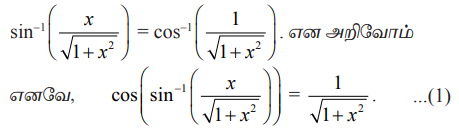
cot−1 (3/4) = θ. என்க. பின்னர் cot θ = ¾ மற்றும் θ குறுங்கோணம்.

படத்திலிருந்து, நமக்கு கிடைக்கபெறுவது

sin {cot −1 (3/4)} = sin θ = 4/5     ………………..(2)

(1) மற்றும் (2)−ஐ கொடுக்கப்பட்ட சமன்பாட்டில் பயன்படுத்தும்போது

1/√(1 + x2)  = 4/5 , என்பதிலிருந்து √[1 + x2 ] = 5/4 எனவே, x = ±3/4.