வடிவியல் விளக்கம் - மூன்று கணங்களின் கார்டீசியன் பெருக்கல் | 10th Mathematics : UNIT 1 : Relation and Function

10வது கணக்கு : அலகு 1 : உறவுகளும் சார்புகளும்

மூன்று கணங்களின் கார்டீசியன் பெருக்கல்

A, B, C ஆகியவை வெற்றில்லா கணங்கள் எனில், அதன் கார்டீசியன் பெருக்கற்பலனின் கணமானது அனைத்து சாத்தியமான வரிசையில் அமைந்த மூன்றின் தொகுதிகளின் கணமாகும். A × B × C = {(a, b, c) அனைத்து a ∈ A, b ∈ B, c ∈ C}

மூன்று கணங்களின் கார்டீசியன் பெருக்கல் (Cartesian Product of three Sets)

A, B, C ஆகியவை வெற்றில்லா கணங்கள் எனில், அதன் கார்டீசியன் பெருக்கற்பலனின் கணமானது அனைத்து சாத்தியமான வரிசையில் அமைந்த மூன்றின் தொகுதிகளின் கணமாகும்.

A × B × C = {(a, b, c) அனைத்து a ∈ A, b ∈ B, c ∈ C}

இரண்டு மற்றும் மூன்று கணங்களுக்கான கார்டீசியன் பெருக்கலின் வடிவியல் விளக்கம்

A = {0, 1}, B = {0, 1}, C = {0, 1} என்க

A × B = {0, 1} × {0, 1} = {(0, 0), (0,1), (1, 0), (1,1)}

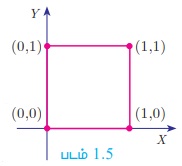
A × B ஆனது XY- தளத்தில் (plane) குறிக்கப்பட்டுள்ளதைப் படம் 1.5-ல் காணலாம்.

(A × B) × C = {(0, 0), (0,1), (1, 0), (1,1)} × {0,1}

= {(0, 0, 0), (0, 0,1), (0,1, 0), (0,1,1), (1, 0, 0), (1, 0,1) (1,1, 0), (1,1,1)}

A × B × C ஆனது XYZ - என்ற வெளியில் (space) குறிக்கப்பட்டுள்ளதைப் படம் 1.6 ல் காணலாம்.

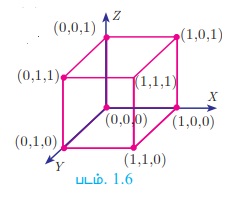
A × B என்பது இரு பரிமாணத்தில் சதுரத்தின் புள்ளிகளைக் குறிக்கிறது. A × B × C என்பது முப்பரிமாணத்தில் கனசதுரத்தின் புள்ளிகளைக் குறிக்கிறது.

குறிப்பு

பொதுவாக, இரண்டு வெற்றில்லா கணங்களின் கார்டீசியன் பெருக்கல் இரு பரிமாணங்களைக் கொண்ட வடிவத்தை ஏற்படுத்தும். அதேபோல் மூன்று வெற்றில்லா கணங்களின் கார்டீசியன் பெருக்கல் மூன்று பரிமாணங்களைக் கொண்ட முப்பரிமாணப் பொருளை ஏற்படுத்தும்.

Tags : Illustration for Geometrical understanding வடிவியல் விளக்கம் .

10th Mathematics : UNIT 1 : Relation and Function : Cartesian Product of three Set Illustration for Geometrical understanding in Tamil : 10th Standard TN Tamil Medium School Samacheer Book Back Questions and answers, Important Question with Answer. 10வது கணக்கு : அலகு 1 : உறவுகளும் சார்புகளும் : மூன்று கணங்களின் கார்டீசியன் பெருக்கல் - வடிவியல் விளக்கம் : 10 ஆம் வகுப்பு தமிழ்நாடு பள்ளி சமசீர் புத்தகம் கேள்விகள் மற்றும் பதில்கள்.