சார்புகள்

சார்புகள் (Functions) 

இரண்டு வெற்றில்லா கணங்களுக்கு இடையேயான பல உறவுகளில் சில குறிப்பிட்ட உறவுகளைச் சார்புகள் என்கிறோம்.

விளக்கம் 8 

ஒரு நிறுவனத்தில் 5 பணியாளர்கள் வெவ்வேறு பிரிவுகளில் உள்ளனர். அவர்களது மாத ஊதிய விநியோகத்தை படம் 1.11 மூலம் நாம் காணலாம். இங்கு ஒரு பணியாளருக்கு ஒரு ஊதியம் மட்டுமே தொடர்புடையதாக இருப்பதைக் காண முடிகிறது.

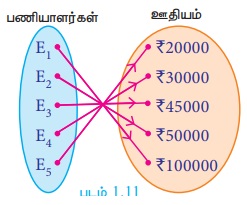
குறிப்பிட்ட சிறப்பு உறவுகளைக் கீழ்க்காணும் வாழ்வியல் சூழல் மூலம் காணலாம். 

1. உன் வகுப்பு மாணவர்களின் கணத்தை A எனக் கொள்க. ஒவ்வொரு மாணவருக்கும் ஒரே ஒரு வயதுதான் இருக்க முடியும். 

2. நீ கடைக்குச் சென்று ஒரு புத்தகம் வாங்கு. அப்படி வாங்கும் புத்தகத்திற்கு ஒரே ஒரு விலை மட்டுமே இருக்கும். ஒரே புத்தகத்திற்கு இரண்டு விலைகள் இருக்காது. (பல புத்தகங்களுக்கு ஒரே விலை இருக்கலாம்). 

3. உங்களுக்குப் பாயிலின் விதி பற்றி தெரிந்திருக்கும். கொடுக்கப்பட்ட ஒவ்வோர் அழுத்தம் P -க்கு ஒரே ஒரு கனஅளவு V மட்டுமே இருக்கும். 

4. பொருளாதாரத்தில், தேவையான பொருளின் எண்ணிக்கையை Q = 360 − 4P, எனக் குறிப்பிடுவோம். இங்கு P என்பது பொருளின் விலை. P-யின் ஒவ்வொரு மதிப்பிற்கும், ஒரே ஒரு Q - மதிப்பு மட்டுமே கிடைக்கும். எனவே தேவையான பொருளின் எண்ணிக்கை Q ஆனது அப்பொருளின் விலை P-யைப் பொருத்து அமைகிறது. 

நாம் இதைப்போன்ற உறவுகளை அடிக்கடி கடந்து வருகின்றோம். இங்கு A- என்ற கணத்தில் உள்ள ஒவ்வொரு உறுப்பிற்கும் B-ல் ஒரே ஒரு உறுப்பு மட்டுமே தொடர்புடையதாக உள்ளது. இத்தகைய உறவுகளையே "சார்புகள்" என்கிறோம். நாம் சார்பை f  எனக் குறிப்பிடுவோம்.

வரையறை

X மற்றும் Y என்ற வெற்றில்லா கணங்களுக்கிடையேயான ஒரு உறவு f -ல் ஒவ்வொரு x ∈ X - க்கும் ஒரே ஒரு y ∈Y கிடைக்கிறது எனில், ' f ' ஐ நாம் "சார்பு" என்கிறோம். 

அதாவது, f = {(x, y) |  ஒவ்வொரு x ∈ X -க்கும், ஒரே ஒரு y ∈ Y இருக்கும்}.

X -லிருந்து Y-க்கான சார்பை, f : X → Y என எழுதலாம்.

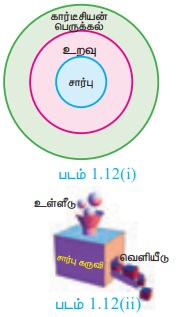
உறவு மற்றும் சார்பு ஆகியவற்றை ஒப்பிட்டுப் பார்க்கும்போது ஒவ்வொரு சார்பும் உறவே. எனவே, சார்புகள் உறவின் உட்கணமாகும். உறவுகள் கார்டீசியன் பெருக்கலின் உட்கணமாகும். (படம் 1.12(i))

ஒரு சார்பு f ஐ இயந்திரமாகக் கருதினால் (படம் 1.12(ii)) ஒவ்வொரு உள்ளீடு x - ம் ஒரே ஒரு தனிப்பட்ட வெளியீடு f(x) -ஐ கொடுக்கின்றது.

உங்களுக்குத் தெரியுமா?

ஒரு சார்பை, தொடர்புபடுத்துதல் அல்லது உருமாற்றம் செய்தல் எனக் கருதலாம்.

குறிப்பு 

f : X → Y ஆனது ஒரு சார்பு எனில், 

· கணம் X ஐ, சார்பு f -ன் மதிப்பகம் என்கிறோம் மற்றும் கணம் Y ஐ, அதன் துணைமதிப்பகம் என்கிறோம். 

· f (a) = b - ஆக இருந்தால் சார்பு f-ல் b -ஆனது, a-யின் "நிழல் உரு" எனவும் மற்றும் a ஆனது, b-யின் "முன் உரு" எனவும் அழைக்கிறோம்.

· X-யின் அனைத்து நிழல் உருக்களையும் கொண்ட கணத்தை f-யின் வீச்சகம் என்கிறோம். 

· f : X → Y ஆனது ஒரு சார்பு எனில்,

(i) மதிப்பகத்தில் உள்ள ஒவ்வொரு உறுப்பிற்கும் நிழல் உரு இருக்கும். 

(ii) ஒவ்வொரு உறுப்பிற்கும் ஒரே ஒரு நிழல் உருதான் இருக்கும். 

· முடிவுறு கணங்கள் A யிலிருந்து B-க்கு n(A) = p, n(B) = q எனில், A மற்றும் B-க்கு இடையேயான மொத்தச் சார்புகளின் எண்ணிக்கை qp ஆகும். 

· இந்தப் பாடப்பகுதியில் f என்ற சார்பின் வீச்சகத்தை மெய்யெண்களின் உட்கணமாக நாம் கருதிக்கொள்ளலாம். 

· சார்பின் மதிப்பகத்தை விளக்கும்போது 

i) f (x) = 1 / [x + 1]. –யில் x = -1 எனில் f (-1) வரையறுக்க முடியாது. எனவே f ஆனது x = -1 தவிர அனைத்து மெய்யெண்களுக்கும் வரையறுக்கப்படுகின்றது. ஆகையால், f -ன் மதிப்பகமானது R - {-1}.

(ii) f (x) =, 1 / x2 – 5x + 6 -ல் x = 2,3 ஆக இருந்தால், f (2) மற்றும் f (3) -ஐ வரையறுக்க முடியாது. எனவே, f ஐ x = 2 மற்றும் 3 தவிர அனைத்து மெய்யெண்களுக்கு வரையறுக்கலாம். ஆகையால், f-யின் மதிப்பகம் = R - {2,3}.

முன்னேற்றச் சோதனை

1. உறவுகள் _____ ன் உட்கணமாகும். சார்புகள் _______ ன் உட்கணமாகும். 

2. சரியா அல்லது தவறா: ஓர் உறவின் எல்லா உறுப்புகளுக்கும் நிழல் உரு இருக்கும். 

3. சரியா அல்லது தவறா: ஒரு சார்பின் எல்லா உறுப்புகளுக்கும் நிழல் உரு இருக்கும். 

4. சரியா அல்லது தவறா: R : A → B ஆனது ஒரு உறவு எனில், R -ன் மதிப்பகம் A ஆகும். 

5. f : ℕ – ℕ என வரையறுக்கப்பட்டால், f(x) = x2 -ல் 1 மற்றும் 2 நிழல் உரு(க்கள்) ________ மற்றும் __________

6. உறவிற்கும் சார்பிற்கும் இடையேயான வேறுபாடு என்ன? 

7. A மற்றும் B ஆகியவை இரண்டு வெற்றில்லா முடிவுற்ற கணங்கள் என்க. பின்வருவனவற்றுள் எந்தத் தொகுப்பு பெரியதாக இருக்கும்? 

(i) A மற்றும் B -க்கு இடையேயான உறவுகளின் எண்ணிக்கை 

(ii) A மற்றும் B-க்கு இடையேயான சார்புகளின் எண்ணிக்கை

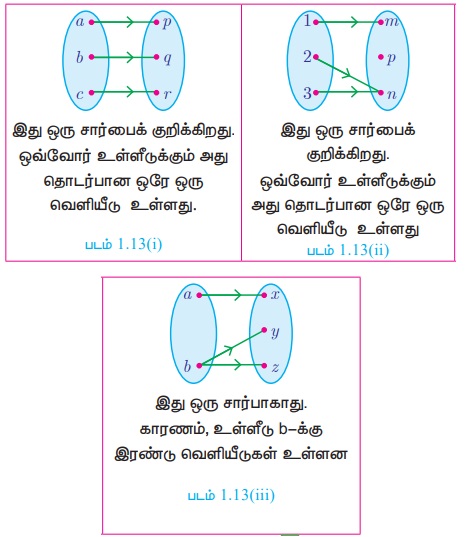
விளக்கம் 9 - சார்புகளுக்கான சோதனை 

அம்புக்குறி படத்தில் காணுதல் 

கணிதத்தில் உயரிய கோட்பாடுகளைப் புரிந்து கொள்வதில், சார்புகள் முக்கியப் பங்கு வகிக்கின்றன. சார்புகள் ஒரு வடிவிலிருந்து மற்றொரு வடிவிற்கு மற்றும் அடிப்படைக் கருவியாகிறது. இதனால், பொறியியல் அறிவியலில் சார்புகள் அதிக அளவில் பயன்படுத்தப்படுகின்றன. 

குறிப்பு

ஒரு சார்பின் வீச்சகமானது அதன் துணை மதிப்பகத்தின் உட்கணமாகும்

எடுத்துக்காட்டு 1.6

X = {1,2,3,4}, y = {2,4, 6, 8,10} மற்றும் R = {(1,2), (2,4), (3,6), (4,8)} எனில், R ஆனது ஒரு சார்பு எனக் காட்டுக. மேலும் அதன் மதிப்பகம், துணை மதிப்பகம் மற்றும் வீச்சகத்தைக் காண்க 

தீர்வு 

படம் 1.14-ல் R குறிக்கப்பட்டுள்ளது. ஒவ்வொரு x ∈ X - க்கும், ஒரே ஒரு y ∈Y உறுப்பு மட்டும் கிடைக்கிறது. எனவே X-ன் எல்லா உறுப்புகளுக்கும் Y-ல் ஒரே ஒரு நிழல் உரு உள்ளது. எனவே R-ஆனது ஒரு சார்பு ஆகும்.

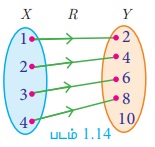
மதிப்பகம் X = {1,2,3,4}; துணை மதிப்பகம் Y = {2,4,6,8,10}; வீச்சகம் f = {2,4,6,8}. 

எடுத்துக்காட்டு 1.7 

f:X→Y என்ற உறவானது f(x) = x2 - 2 என வரையறுக்கப்படுகிறது. இங்கு, X = {-2, -1, 0, 3} மற்றும் Y = R எனக் கொண்டால் (i) f-யின் உறுப்புகளைப் பட்டியலிடுக. (ii) f - ஒரு சார்பாகுமா? 

தீர்வு 

f (x) = x2  – 2 இங்கு X = {−2,−1, 0, 3} 

(i) f (-2) = (-2)2 - 2 = 2; f (-1) = (-1)2 - 2 = -1

f (0) = (0)2 - 2 = -2; f(3) = (3)2 - 2 = 7

⸫     f = {(-2,2), (-1,-1), (0,-2), (3,7)} 

(ii) f -யின் ஒவ்வொரு மதிப்பக உறுப்பிற்கும் ஒரே ஒரு நிழல் உரு உள்ளதைக் காணலாம். எனவே f -ஆனது ஒரு சார்பாகும்.

சிந்தனைக் களம் 

கோள்களுக்கும் அதன் துணைக்கோள்களுக்கும் இடையே உள்ள தொடர்பு சார்பாகுமா?

எடுத்துக்காட்டு 1.8 

X = {-5,1,3,4} மற்றும் Y = {a,b,c} எனில், X -லிருந்து Y-க்கு பின்வரும் உறவுகளில் எவை சார்பாகும்?

(i) R1 = {(–5,a), (1,a), (3,b)}

(ii)   R 2 = {(–5,b), (1,b), (3,a),(4,c)}

(iii)  R 3  = {(–5,a), (1,a), (3,b),(4,c),(1,b)}

தீர்வு 

(i) R1 = {(–5,a), (1,a), (3,b)}

R1 -க்கான உறவை அம்புக்குறி படத்தில் குறிக்கலாம் (படம் 1.15(i)).

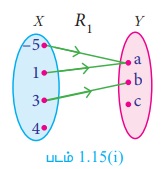
R1 சார்பாகாது. காரணம் 4 ∈ X -க்கு Y-ல் நிழல் உரு இல்லை. 

(ii) R2 = {(–5,b), (1,b), (3,a),(4,c)}

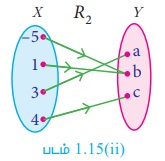
R2 -க்கான உறவை அம்புக்குறி படத்தில் குறிக்கலாம் (படம் 1.15 (ii)). 

R2 ஒரு சார்பாகும். காரணம் X-யின் ஒவ்வொரு உறுப்புக்கும் ஒரே ஒரு நிழல் உரு Y-ல் உள்ளது.

(iii) R3 = {(–5,a), (1,a), (3,b),(4,c),(1,b)}

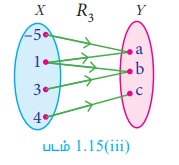
R3 -க்கான உறவை அம்புக்குறி படத்தில் குறிக்கலாம் (படம் 1.15 (iii)). 

R3 ஒரு சார்பாகாது. காரணம் 1 ∈ X -க்கு இரண்டு நிழல் உருக்கள் a ∈Y மற்றும் b ∈Y என உள்ளன. 

இவற்றின் மூலம், ஓர் உறுப்பிற்கு, ஒரே ஒரு நிழல் உரு இருந்தால் மட்டுமே அந்த உறவு சார்பாகும் என அறியலாம்.

எடுத்துக்காட்டு 1.9

f(x) = 2x – x2 எனக் கொடுக்கப்பட்டுள்ளது எனில், 

(i) f (1) (ii) f (x+1) (iii) f (x) + f (1) ஆகியவற்றைக் காண்க

தீர்வு 

(i) x = 1 எனப் பிரதியிட்டால்,

f (1) = 2(1) - (1)2 = 2 – 1 = 1 

(ii) x = x + 1 எனப் பிரதியிட்டால்,

f (x + 1) = 2(x + 1) - (x + 1)2 = 2x + 2 – (x2 + 2 x + 1) = - x2 + 1 

(iii) f (x) + f (1) = (2x – x2) + 1 = −x2 + 2x + 1

[f (x ) + f (1) ≠ f (x + 1) என்பதைக் காணலாம். பொதுவாக, f (a +b) ஆனது f(a) + f(b) - க்கு சமமாக இருப்பதில்லை]