சார்புகளின் வகைகள்

சார்புகளின் வகைகள் (Types of Functions)

இந்தப் பகுதியில் கீழ்க்கண்ட சார்புகளின் வகைகளைப் பற்றி தகுந்த எடுத்துக்காட்டுடன் காணலாம்.

(i) ஒன்றுக்கு - ஒன்றான (one - one) 

(ii) பலவற்றிற்கு - ஒன்று (many - one) 

(iii) மேல் (onto)

(iv) உள்நோக்கிய (into)

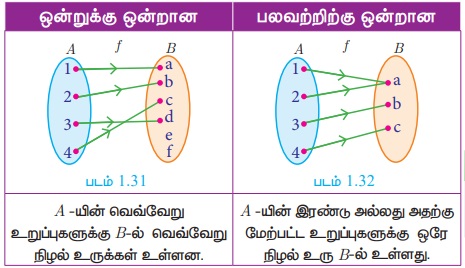
1. ஒன்றுக்கு ஒன்றான சார்பு (One - one function)

நம்மிடம் நன்கு வேலை செய்யும் அலைபேசி ஒன்று உள்ளது எனக் கொள்க. உங்கள் நண்பனுக்கு ஒரு சாதாரணத் தொடர்பின் மூலம் பேசுவதற்கு ஒரு நேரத்தில், ஒரு முறை தான் தொடர்பு கொள்ள முடியும் (படம் 1.21)

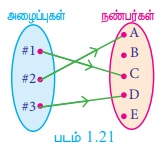
நாம் பேசுவதற்குத் தொடர்பு கொள்ளும் எண்ணை ஒரு சார்பாகக் கொண்டால், அது ஒன்றுக்கு ஒன்றான சார்பு எனக் கூறலாம்.

f : A → B என்பது ஒரு சார்பு என்க. A -யின் வெவ்வேறான உறுப்புகளை B -ல் உள்ள வெவ்வேறு உறுப்புகளுடன் f ஆனது தொடர்புபடுத்துமானால், f என்பது ஒன்றுக்கு ஒன்றான சார்பு ஆகும்.

ஒன்றுக்கு ஒன்றான சார்பு என்பது ஒருபுறச் சார்பு (Injective function) எனவும் அழைக்கப்படும். இதற்குச் சமமாக,

f(a1) = f(a2) என்றவாறு அமைந்த ஒவ்வொரு a1, a2 ∈ A -க்கும் a1 = a2 எனக் கிடைத்தால், f என்பது ஒன்றுக்கொன்றான சார்பாகும்.

விளக்கம் 10

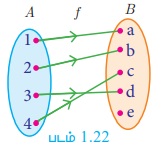
A = {1,2,3,4} மற்றும் B = {a, b, c, d, e} 

(i) f = {(1, a), (2, b), (3, d), (4, c)} எனில், படம் 1.22-ல் A-யின் வெவ்வேறு உறுப்புகளுக்கு B-ல் வெவ்வேறு நிழல் உருக்கள் உள்ளன.

எனவே f ஆனது ஒன்றுக்கொன்றான சார்பாகும்.

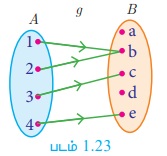
(ii) g = {(1,b), (2,b), (3,c), (4,e)} 

படம் 1.23 -ல் g ஆனது A-விலிருந்து B -க்கு ஒரு சார்பு. மேலும் g(1) = g(2) = b, ஆனால் 1 ≠ 2. எனவே, கணம் A-ல் 1 மற்றும் 2 ஆகிய இரண்டு வெவ்வேறு உறுப்புகளுக்குக் கணம் B -ல் 'b' என்ற ஒரே ஒரு நிழல் உருதான் உள்ளது. எனவே g ஆனது ஒன்றுக்கு ஒன்றான சார்பு அல்ல.

2. பலவற்றிற்கு ஒன்றான சார்பு (Many - one function) 

ஒரு திரையரங்க வளாகத்தில் F1, F2, F3 என்ற மூன்று திரைப்படங்கள் திரையிடப்படுகின்றன. ஏழு நபர்கள் (P1 -லிருந்து P7 வரை) திரையரங்கிற்கு வந்து காட்சி சீட்டு வாங்கும் விதம் (படம் 1.24)-ல் காட்டப்பட்டுள்ளது.

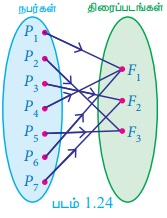
நாம் திரைப்படத்தைத் தேர்வு செய்வதை ஓர் உறவாகக் கொண்டால் அது பலவற்றிற்கு ஒன்றான சார்பாக விளங்கும். காரணம் ஒருவருக்கு ஒரு காட்சிச் சீட்டு மட்டுமே கொடுக்கப்படும், ஆனால் ஒரே படத்தைப் பார்க்க பலர் தேர்வு செய்யலாம். 

சார்பு f : A→ B -ஐ பலவற்றிற்கு ஒன்றான சார்பு எனில், அச்சார்பில் A-யின் ஒன்றிற்கு மேற்பட்ட உறுப்புகளுக்கு, B-ல் ஒரே நிழல் உரு இருக்கும்.

f : A→B எனும் சார்பில், f ஆனது ஒன்றுக்கு ஒன்றாக இல்லையெனில், அது பலவற்றிக்கு ஒன்று எனக் கூறலாம். 

விளக்கம் 11

A = {1,2,3,4} மற்றும் B = {a,b,c} என்க. f  = {(1,a), (2,a), (3,b), (4,c)} என்க. 

f என்ற சார்பில் 1 மற்றும் 2 என்ற, A-யில் உள்ள உறுப்புகளுக்கு B-யில் ஒரே நிழல் உரு 'a' ஆக இருப்பதால், சார்பு f ஆனது பலவற்றிற்கு - ஒன்றான சார்பாகும். 

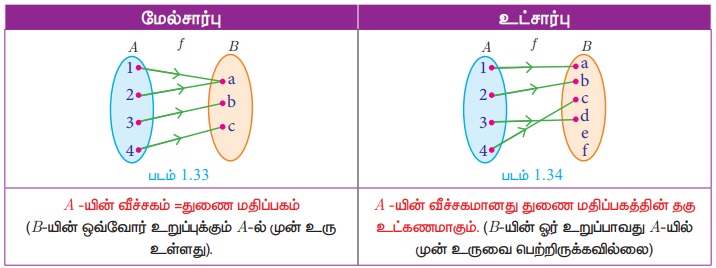
3. மேல் சார்பு (Onto function)

ஒரு கைபேசியில் மூன்று நபர்களின் பெயர்கள் பதிவில் உள்ளன எனக் கொள்க. பதிவில் உள்ள மூவருக்கும் அழைப்புகள் செல்கின்றன எனில், அந்த அழைப்புகளை குறிக்கும் சார்பு மேல் சார்பு (படம் 1.25) ஆகும்.

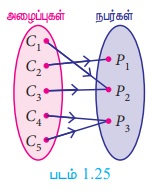
f : A→ B என்ற ஒரு சார்பு, மேல் சார்பு எனில், f -யின் வீச்சகமானது, f -யின் துணை மதிப்பகத்திற்குச் சமமாக இருக்கும்.

துணை மதிப்பகம் B-ல் உள்ள ஒவ்வோர் உறுப்பிற்கும் மதிப்பகம் A-ல் முன் உரு இருக்கும் எனவும் கூறலாம். 

இதை மேல்புறச் சார்பு (Surjective function) எனவும் அழைக்கலாம்.

குறிப்பு

f : A → B ஆனது மேல் சார்பு எனில், f -யின் வீச்சகம் = B

விளக்கம் 12 

A = {x, y, z}, B = {l, m, n} என்க 

f-ன் வீச்சகம் = {l, m, n} = B (படம்.1.26) 

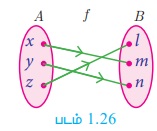
எனவே, f ஆனது ஒரு மேல் சார்பாகும். 

4. உட்சார்பு (Into function)

ஒரு வீட்டு உபயோகப் பொருள்கள் விற்பனையகத்தில். புது வருட விற்பனைக்காக, தொலைக்காட்சிப் பெட்டி, காற்று பதனி (Air Conditioner), சலவை இயந்திரம் (Washing machine) மற்றும் நீர்ச் சூடேற்றி (Water heater) ஆகியவற்றிற்கு 20% தள்ளுபடி செய்து சலுகை வழங்கியுள்ளது. மேற்கண்ட பொருள்களை C1, C2, C3 என்ற மூன்று நுகர்வோர் தேர்வு செய்வதாக எடுத்துக்கொண்டால், அதை ஒரு சார்பாகக் கொள்ளலாம். (படம் 1.27) மேலும், இது உட்சார்பைக் குறிக்கின்றது.

சாதாரணமாக, குளிர் காலத்தில் நுகர்வோர் காற்று பதனியை தேர்வு செய்யமாட்டார்கள். எனவே, இது உட்சார்புக்கு எடுத்துக்காட்டாகும்.

ஒரு சார்பு f : A→ B ஆனது உட்சார்பு எனில், B-ல் குறைந்தபட்சம் ஓர் உறுப்பிற்காவது, A-ல் முன்உரு இருக்காது.

f-ன் வீச்சகமானது துணை மதிப்பகத்தின் தகு உட்கணமாகும். எனவே, f: A→ B ஆனது மேல்சார்பு இல்லையெனில் அது உட்சார்பாகும்.

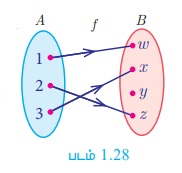
விளக்கம் 13

A = {1,2,3,} மற்றும் B = {w, x, y, z} என்க. சார்பு f  = {(1,w), (2, z), (3,x)} என்க.

இங்கு, f-ன் வீச்சகம் f  = {w,  x,  z} ⊂ B (படம்.1.28) என்பதால், f ஆனது உட்சார்பு ஆகும். y ∈ B -க்கு முன் உரு A-ல் இல்லை என்பதை நோக்குக.

5. இருபுறச் சார்பு (Bijection)

ஒரு வட்டத்தைப் படம் 1.29-ல் உள்ளபடி எடுத்துக்கொண்டால், வட்டத்தின் உட்பகுதியில் உள்ள ஒவ்வொரு ஆங்கில எழுத்திற்கும் மற்றொரு ஆங்கில எழுத்து அதன் வெளிப்புறத்தில் மாற்றி அமைக்கப்பட்டுள்ளதைக் காணலாம். 

எனவே A → D, B → E, C  → F , …  Z → C.  இந்த வட்டத்தைக் குறியீட்டு வட்டம் (Cipher circle) என்கிறோம். இதை வைத்து, நாம் 'HELLO' என்ற வார்த்தையை 'KHOOR' என மாற்றம் செய்கிறோம். இதே வட்டத்தைப் பயன்படுத்தி வெளியே உள்ள எழுத்திற்குப் பதிலாகத் திரும்பவும் உள்ளே உள்ள எழுத்தை மாற்றுகின்றோம் எனில், 'KHOOR' என்ற வார்த்தை மீண்டும் 'HELLO’ -வாக கிடைத்துவிடும். இத்தகைய நிகழ்ச்சியைத் தான் இருபுறச் சார்பு என்கிறோம். இவ்விதமான இரகசியக் குறியீடுகளைப் பயன்படுத்துவதற்கான முறையை குழுக் குறியியல் (Cryptography) என்கிறோம்.

f : A→ B என்ற சார்பு, ஒன்றுக்கு ஒன்றாகவும் மற்றும் மேல்சார்பாகவும் இருந்தால் f -ஐ A-லிருந்து B-க்கான இருபுறச் சார்பு என்கிறோம்.

விளக்கம் 14

விளக்கம் 15

குறிப்பு

ஒரு சார்பு ஒன்றுக்கு ஒன்றான மற்றும் மேல் சார்பாக இருந்தால் நாம் அதை ஒன்றுக்கு ஒன்றான தொடர்பு எனவும் கூறலாம்.

சிந்தனைக்களம்

ஒன்றிற்குப் பல என்ற சார்பு இருக்க முடியுமா?

கொடுக்கப்பட்ட சார்பு ஒன்றுக்கு ஒன்றா அல்லது இல்லையா என அறிவதற்குக் கீழ்க்காணும் சோதனை நமக்குப் பயன்படும்.

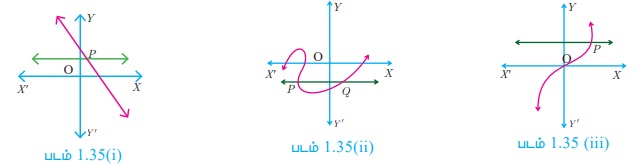
6. கிடைமட்டக்கோட்டுச் சோதனை (Horizontal Line Test)

இதற்கு முன்னர் நாம் குத்துக் கோட்டுச் சோதனையைப் பார்த்தோம். தற்போது கிடைமட்டக்கோட்டுச் சோதனையைப் பார்க்கலாம். "வளைவரை ஒன்றுக்கொன்றான சார்பைக் குறித்தால், வரையப்படும் கிடைமட்டக்கோடு வளைவரையை அதிகபட்சமாக ஒரு புள்ளியில் மட்டுமே வெட்டும்"

எடுத்துக்காட்டு 1.12

கிடைமட்டக்கோடு சோதனையைப் பயன்படுத்தி (படம் 1.35 (i), (1.35 (ii), 1.35 (iii)), கீழ்க்கண்ட சார்புகளில் எவை ஒன்றுக்கொன்றானவை எனக் காண்க.

தீர்வு 

ஒரு கிடைமட்டக்கோடு, வரைபடம் 1.35 (i) மற்றும் படம் 1.35 (iii) ஆகியவற்றை அதிகபட்சமாக ஒரே ஒரு புள்ளியில் P வெட்டுவதால் இவை ஒன்றுக்கு ஒன்றான சார்பினைக் குறிக்கும்.

வரைபடம் (1.35 (ii))-ல் வரையப்பட்ட ஒரு கிடைமட்டக்கோடு P மற்றும் Q ஆகிய இரு புள்ளிகளில் வெட்டுவதால், கொடுக்கப்பட்ட வளைவரை ஒன்றுக்கு ஒன்றான சார்பைக் குறிக்காது. 

எடுத்துக்காட்டு 1.13 

A = {1,2,3}, B = {4,5,6,7} மற்றும் f = {(1,4), (2,5), (3,6)} ஆனது A-லிருந்து B-க்கான சார்பு ஆகும். f ஆனது ஒன்றுக்கு ஒன்றான சார்பு ஆனால் மேல்சார்பு இல்லை எனக் காட்டுக.

தீர்வு 

A = {1,2,3}, B = {4, 5,6,7}; f = {(1,4), (2,5), (3,6)}

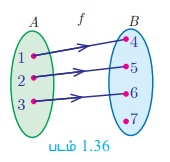
A-லிருந்து B-க்கு ஆன சார்பு f -ல், A-யின் வெவ்வேறு உறுப்புகளுக்கு, B-ல் வெவ்வேறு நிழல் உரு உள்ளது. எனவே, f ஒன்றுக்கு ஒன்றான சார்பாகும். துணை மதிப்பகத்தில் உள்ள உறுப்பு 7-க்கு, மதிப்பகத்தில் முன் உரு இல்லை. எனவே, f ஆனது, மேல் சார்பு இல்லை. (படம் 1.36)

எனவே, f ஆனது ஒன்றுக்கு ஒன்றானது, ஆனால் மேல்சார்பு இல்லை.

எடுத்துக்காட்டு 1.14

A = {-2, -1, 0, 1, 2} மற்றும் f : A → B என்ற சார்பானது f (x) = x2 + x + 1 மேல் சார்பு எனில், B-ஐ காண்க. 

தீர்வு A = {−2, −1, 0, 1, 2} மற்றும் f (x) = x2  + x + 1 கொடுக்கப்பட்டுள்ளது.

f (-2) = (−2)2 + (−2) + 1 =3; f (-1) = (−1)2 + (−1) + 1 = 1

f (0) = 02 + 0 + 1 =1;

f (1) = 12 + 1 + 1 = 3

f (2) =22 + 2+ 1 = 7

எனவே, f -ன் வீச்சகம் B = {1, 3, 7}.

எடுத்துக்காட்டு 1.15 

f : N → N  என்ற சார்பானது f (x) = 3x + 2, x ∈  ℕ எனவரையறுக்கப்பட்டால்

(i) 1, 2, 3 -யின் நிழல் உருக்களைக் காண்க

(ii) 29 மற்றும் 53-யின் முன் உருக்களைக் காண்க. 

(iii) சார்பின் வகையைக் காண்க. 

தீர்வு 

f : N → N என்ற சார்பானது f (x) = 3x + 2 என வரையறுக்கப்பட்டுள்ளது. 

(i) x = 1 எனில், f (1) = 3(1) + 2 = 5

x = 2 எனில், f(2) = 3(2) + 2 = 8

x = 3 எனில், f(3) = 3(3) + 2 = 11

1, 2, 3 -யின் நிழல் உருக்கள் முறையே 5, 8, 11 ஆகும். 

(ii) 29-யின் முன் உரு x எனில், f(x) = 29 . எனவே 3 x + 2 = 29

3 x = 27 ⇒ x = 9. 

இதைப்போலவே, 53 -ன் முன் உரு x எனில், f(x) = 53. எனவே, 3x + 2 = 53 

3 x = 51 ⇒ x = 17.

எனவே, 29 மற்றும் 53 - யின் முன் உருக்கள் முறையே 9 மற்றும் 17 ஆகும். 

(iii) ℕ -யின் வெவ்வேறு உறுப்புகளுக்குத் துணை மதிப்பகத்தில் வெவ்வேறு நிழல் உருக்கள் உள்ளன. எனவே, f ஆனது ஒன்றுக்கு ஒன்றான சார்பாகும். f -யின் துணை மதிப்பகமானது ℕ. 

வீச்சகம் f = {5, 8, 11, 14, 17, ...} ஆனது ℕ-ன் தகு உட்கணமாகும். எனவே, f ஆனது மேல்சார்பு இல்லை.

அதாவது, f உட்சார்பு ஆகும்.

எனவே, f ஆனது ஒன்றுக்கு ஒன்றான மற்றும் உட்சார்பு ஆகும்.

எடுத்துக்காட்டு 1.16 

தடயவியல் விஞ்ஞானிகள், தொடை எலும்புகளைக் கொண்டு ஒருவருடைய உயரத்தை (செ.மீட்டரில்) கணக்கிடுகிறார்கள். அவர்கள் பொதுவாக, h(b) = 2 ⋅ 47b + 54 ⋅ 10 என்ற சார்பை இதற்குப் பயன்படுத்துகிறார்கள். இங்கு, b ஆனது தொடை எலும்பின் நீளமாகும்.

(i) h. ஆனது ஒன்றுக்கு ஒன்றானதா எனச் சரிபார்க்க. 

(ii) தொடை எலும்பின் நீளம் 50 செ.மீ எனில், அந்த நபரின் உயரத்தைக் காண்க. 

(iii) நபரின் உயரம் 147.96 செ.மீ எனில், அவர் தொடை எலும்பின் நீளத்தைக் காண்க.

தீர்வு 

(i) h ஆனது ஒன்றுக்கு ஒன்றானதா எனச் சோதிக்க h(b1) = h(b2) எனக் கருதுக. 

எனவே, நமக்குக் கிடைப்பது, 2 ⋅ 47b1 + 54 ⋅ 10 = 2 ⋅ 47b2 + 54 ⋅ 10

2 × 47b1 = 2 ⋅ 47b2 ⇒ b1  = b2

எனவே, h(b1) = h(b2) எனில், b1 = b2. ஆகையால், இந்தச் சார்பு ஒன்றுக்கு ஒன்றான சார்பாகும்.

(ii) தொடை எலும்பின் நீளம் b = 50 செ.மீ எனில், அந்த நபரின் உயரமானது

h(50) = (2 ⋅ 47 × 50) + 54 ⋅ 10 = 177 ⋅ 6 செ.மீ ஆகும். 

(iii) நபரின் உயரம் 147.96 செ.மீ எனில், h(b) = 147⋅96 தொடை எலும்பின் நீளமானது

2 ⋅ 47b + 54 ⋅ 10 = 147 ⋅ 96 .

b = [ 93 ⋅ 86 / 2 ⋅ 47 ] = 38

ஆகையால், தொடை எலும்பின் நீளமானது 38 செ.மீ ஆகும்.

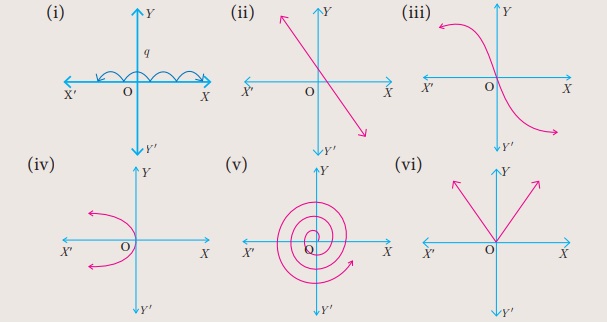
செயல்பாடு 3

பின்வரும் வளைவரைகளில் எவை சார்பினைக் குறிக்கும் எனச் சோதிக்க. சார்பாக இருந்தால் அந்தச் சார்பு ஒன்றுக்கு ஒன்றானதா எனப் பரிசோதிக்க. (குறிப்பு: குத்துக்கோடு, மற்றும் கிடைமட்டக்கோடு சோதனைகளைப் பயன்படுத்துக)