சார்புகளின் சேர்ப்பு

சார்புகளின் சேர்ப்பு (Composition of Functions)

ஓர் ஓட்டுநர், மகிழுந்தின் வேகத்தை கட்டுப்படுத்தும் போது எரிபொருள் பாயும் அளவு குறைந்து மகிழுந்தின் வேகத்தில் மாற்றம் ஏற்படுகின்றது. இதைப்போலவே இரண்டு சார்புகளின் சேர்ப்பு ஒரு 'தொடர் விளைவை' ஏற்படுத்தும் செயலாகும். அதாவது இங்குச் சார்புகள் ஒன்றிற்குப் பிறகு ஒன்றாகச் செயல்படுத்தப்படுகிறது. (படம் 1.40)

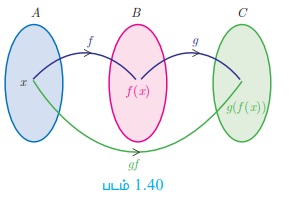
இதை மேலும் விவரிக்க வேண்டுமென்றால், சார்பானது ஒரு நிகழ்வாகும். f மற்றும் g ஆனது இரண்டு சார்புகள் எனில், சார்புகளின் சேர்ப்பு g(f (x)) பின்வருமாறு இருநிலைகள் மூலம் காணலாம்.

(i) f-க்கு x என்ற உள்ளீட்டை வழங்குக; 

(ii) f(x) என்ற f -யின் வெளியீட்டை g -யின் உள்ளீடாகச் செலுத்துக. வெளியீடை g(f (x)) என அழைக்கிறோம் 

விளக்கம்

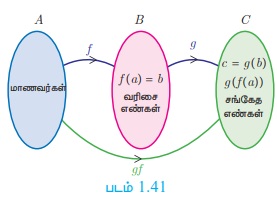
10-ஆம் வகுப்பு பொதுத் தேர்வு எழுதிய மாணவர்களைக் கொண்ட கணம் A என எடுத்துக்கொள்ளலாம். பொதுத்தேர்வு எழுதும் ஒவ்வொரு மாணவருக்கும் வரிசை எண்கள் கொடுக்கப்பட்டுள்ளன. தேர்வுத் துறை ரகசியமாக, அந்த வரிசை எண்ணிற்குப் பதிலாகச் சங்கேத எண்ணைக் கொடுத்துள்ளது. 

A என்ற கணமானது பொதுத்தேர்வு எழுதும் மாணவர்களின் கணமாகும். B ⊆ N என்பது வரிசை எண்களின் கணம் மற்றும் C ⊆ N என்பது சங்கேத எண்களின் (Code number) கணம் என்க. படம் 1.41-ன் இதன் மூலம் இரண்டு சார்புகள் f: A → B மற்றும் g : B → C கிடைக்கப் பெறுகின்றன. b = f (a) ஆனது மாணவர் a-க்கு கொடுக்கப்பட்ட வரிசை எண் ஆகும். c = g(b) ஆனது வரிசை எண்ணிற்குக் கொடுக்கப்பட்ட சங்கேத எண் எனவும் கொள்க. இங்கு a ∈ A , b ∈ B  மற்றும் c ∈ C. இதை c = g(b) = g(f (a)). எனவும் எழுதலாம்.

எனவே, f, g ஆகிய இரண்டு சார்புகளின் சேர்ப்பினால் மாணவர் சங்கேத எண்ணுடன் இணைக்கப்படுகிறார். இதிலிருந்து கிடைப்பதே பின்வரும் வரையறையாகும்.

வரையறை 

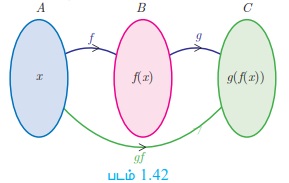
f : A → B மற்றும் g : B → C ஆகியன இரண்டு சார்புகள் எனில், (படம் 1.42) f மற்றும் g-ன் சார்புகளின் சேர்ப்பு g o  f  -ஐ g o  f (x ) = g( f (x )) ∀  x ∈ A  என வரையறுக்கலாம். 

எடுத்துக்காட்டு 1.19

f (x) = 2x + 1, மற்றும் g(x) = x2 – 2 எனில், f o g மற்றும் g o f -ஐ காண்க.

தீர்வு 

f (x) = 2x + 1, g(x) = x2 – 2

f o g(x) = f (g(x)) = f (x2 − 2) = 2(x2 − 2) + 1 = 2x2 – 3

g o f (x) = g(f (x)) = g(2x + 1) = (2x + 1)2 − 2 = 4x2 + 4x – 1

எனவே  f o g = 2x2 − 3, g o f = 4x2 + 4x − 1. மேற்கண்டவற்றிலிருந்து  f o g ≠ g o f என அறிகிறோம்..

சிந்தனைக் களம் 

f (x) = xm மற்றும் g(x) = xn எனில், f o g = g o f ?

குறிப்பு 

பொதுவாக, ஏதேனும் இரு சார்புகள் f மற்றும் g -க்கு, f o g ≠ g o f ஆகும். எனவே சார்புகளின் சேர்ப்புச் செயலி பரிமாற்று விதியைப் பூர்த்தி செய்வதில்லை.

எடுத்துக்காட்டு 1.20

f (x) = 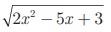-ஐ இரு சார்புகளின் சேர்ப்பாகக் குறிக்க. 

தீர்வு

f2 (x) = 2x2 − 5x + 3 மற்றும்  f1 (x) = √x என வரையறுப்போம். 

எனவே,

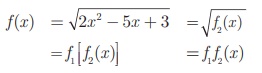
எடுத்துக்காட்டு 1.21 

If f (x) = 3x − 2, g(x) = 2x + k மற்றும் f o g = g o f  எனில், k யின் மதிப்பைக் காண்க. 

தீர்வு 

f (x) = 3x − 2, g(x) = 2x + k

f o g(x) = f (g(x)) = f (2x + k) = 3(2x + k) − 2 = 6x + 3k – 2

எனவே, f o g(x) = 6x + 3k – 2.

g o f (x) = g(3x − 2) = 2(3x − 2) + k

எனவே, g o f (x) = 6x − 4 + k .

f o g = g o f எனக் கொடுக்கப்பட்டுள்ளது.

6x + 3k − 2 = 6x − 4 + k

6x − 6x + 3k − k = −4 + 2 ⇒ 2 k = -2 ⇒ k = −1

உங்களுக்குத் தெரியுமா?

மதிப்பகம் g –யின் உட்கணமாக, g – யின் வீச்சகம் f ஆக இருந்தால் மட்டுமே சார்புகளின் சேர்ப்பு g o f(x) இருக்கும்.

எடுத்துக்காட்டு 1.22 

f o f (k) = 5, f (k) = 2k – 1. எனில், k - யின் மதிப்பைக் காண்க. 

தீர்வு 

f  o f (k) = f (f (k))

= 2(2k − 1) − 1 = 4k − 3

எனவே, f  o f (k) = 4k – 3

ஆனால் f o f (k) = 5 எனக் கொடுக்கப்பட்டுள்ளது.

4k - 3 = 5 ⇒ k = 2

மூன்று சார்புகளின் சேர்ப்பு (Composition of three functions)

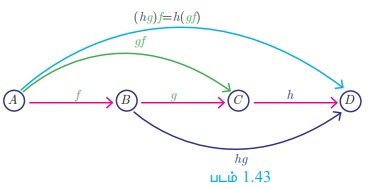
A, B, C, D ஆகியவை நான்கு கணங்கள் மற்றும் f  : A → B ,   g : B → C மற்றும்   h  : C → D ஆகியவை மூன்று சார்புகள் என்க. சார்புகளின் சேர்ப்பு (படம் 1.43) f o g மற்றும் g o h, ஆகியவற்றைப் பயன்படுத்தி இரண்டு புதுச் சார்புகள் (f o g) o h மற்றும் f o (g o h) ஆகியவை கிடைக்கப் பெறலாம். சார்புகளின் சேர்ப்பு பரிமாற்று விதியைப் பூர்த்தி செய்வதில்லை என்பதை நாம் அறிவோம். இது சேர்ப்பு விதியைப் பூர்த்தி செய்யுமா?

குறிப்பு 

மூன்று சார்புகளின் சேர்ப்பானது எப்போதும் சேர்ப்பு விதியைப் பூர்த்தி செய்யும். அதாவது, f o (g o h) = (f o g) o h

எடுத்துக்காட்டு 1.23 

f (x) = 2x + 3 , g(x) = 1 − 2x மற்றும் h(x) = 3x எனில், f o (g o h) = (f o g) o h என நிறுவுக. 

தீர்வு 

f (x) = 2x + 3, g(x) = 1 − 2x, h(x) = 3x

இப்போது, (f o g) (x) = f (g(x)) = f (1 − 2x) = 2(1 − 2x) + 3 = 5 − 4x

மேலும், (f o g) o h(x) = (f o g) (h(x)) = (f o g) (3x) = 5 − 4(3x) = 5 − 12x         ……… (1)

(g o h) (x) = g(h(x)) = g(3x) = 1 − 2(3x) = 1 − 6x

மேலும், f o (g o h) (x) = f (1 − 6x) = 2(1 − 6x) + 3 = 5 − 12x               ………(2)

(1) மற்றும் (2) -லிருந்து, (f o g) o h = f o (g o h)

எடுத்துக்காட்டு 1.24 

f (x) = 3x + 1, g(x) = x + 3 ஆகியவை இரு சார்புகள். மேலும் gff(x) = fgg(x) எனில் x -ஐக் காண்க. 

தீர்வு

gff(x) = g [f {f (x)}]

= g [ f (3x +1)] = g [ 3(3x +1) +1] = g (9x + 4)

g (9x + 4) = [ (9x + 4) + 3] = 9x + 7

fgg(x) = f [g {g (x)}] 

= f [ g (x + 3)] = f [ (x + 3) + 3] = f (x + 6)

f (x + 6) = [ 3(x + 6) + 1] = 3x + 19

gff(x) = fgg (x) எனவே, 9x + 7 = 3x + 19. இந்தச் சமன்பாட்டைத் தீர்க்க x = 2.

முன்னேற்றச் சோதனை

பின்வரும் வினாக்களுக்குச் சரியானவற்றைத் தேர்ந்தெடுப்பதன் மூலமாக விடை கூறுக. 

1. சார்புகளின் சேர்ப்பானது பரிமாற்று விதிக்கு உட்பட்டது.

(அ) எப்போதும் உண்மையே 

(ஆ) ஒருபோதும் உண்மையில்லை 

(இ) சில சமயங்களில் உண்மை 

2. சார்புகளின் சேர்ப்பானது சேர்ப்பு விதிக்குட்பட்டது.

(அ) எப்போதும் உண்மையே 

(ஆ) ஒருபோதும் உண்மையில்லை 

(இ) சில சமயங்களில் உண்மை

செயல்பாடு 4

h(x) = f o g(x) எனக் கொடுக்கப்பட்டால் அட்டவணையில் h(x) -ஐ பூர்த்தி செய்க. 

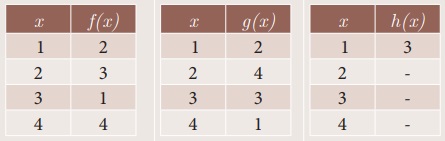
h(1)-ஐ எவ்வாறு கண்டறிவது? 

h(x) = f o g(x) 

h(1) = f o g (1) 

= f(2) = 3 

ஃ h(1) = 3