சார்புகளைக் குறிக்கும் முறை

சார்புகளைக் குறிக்கும் முறை (Representation of Functions)

ஒரு சார்பை 

(i) வரிசைச் சோடிகளின் கணம்

(ii) அட்டவணை முறை 

(iii) அம்புக்குறி படம்

(iv) வரைபட முறை 

ஆகியவற்றின் மூலமாகக் குறிப்பிடலாம் 

f : A → B ஒரு சார்பு என்க. 

(i) வரிசைச் சோடிகளின் கணம்

f = {(x, y) | y = f (x), x ∈ A} என்றவாறு அமையும் அனைத்து வரிசைச் சோடிகளின் கணமாக சார்பு f -ஐ குறிக்கலாம் 

(ii) அட்டவணை முறை

x-ன் மதிப்புகள் மற்றும் f -ஆல் பெறப்படும் நிழல் உருக்கள் ஆகியவற்றைகொண்டு ஒரு அட்டவணையை அமைக்கலாம். 

(iii) அம்புக்குறி படம்

f -ன் மதிப்பகத்தையும் அதன் நிழல் உருக்களையும் அம்புக்குறி மூலம் தொடர்புபடுத்திக் காட்டலாம். 

(iv) வரைபடம்

f = {(x,y)| y = f (x), x ∈ A} -ல் உள்ள அனைத்து வரிசைச் சோடிகளை XY தளத்தில் புள்ளிகளாகக் குறிக்கலாம். அனைத்துப் புள்ளிகளையும் இணைக்கும் படம் f –ன் வரைபடமாகும். 

ஒவ்வொரு சார்பையும், ஒரு வளைவரையாக (curve) வரைபடத்தில் குறிப்பிடலாம். ஆனால் வரைபடத்தில் வரையப்படும் அனைத்து வளைவரைகளும் சார்பாகாது.

ஒரு வளைவரை சார்பாகுமா என்பதைத் தீர்மானிக்க, பின்வரும் சோதனையைப் பயன்படுத்தலாம்.

குத்துக்கோட்டுச் சோதனை (Vertical line test) 

ஒரு வளைவரையை, ஒவ்வொரு குத்துக்கோடும் அதிகபட்சம் ஒரு புள்ளியில் வெட்டினால், அவ்வளைவரை ஒரு சார்பினைக் குறிக்கும்.

எடுத்துக்காட்டு 1.10 

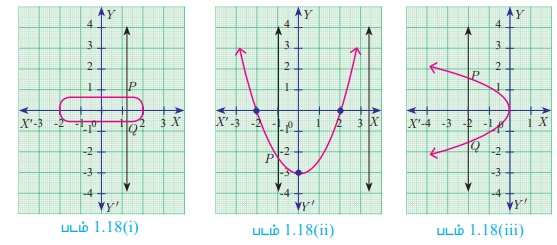
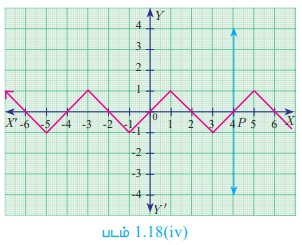
குத்துக்கோடு சோதனையைப் பயன்படுத்திப் பின்வரும் வரைபடங்களில் எவை சார்பினைக் குறிக்கும் எனத் தீர்மானிக்கவும். (படம்.1.18 (i), 1.18 (ii), 1.18 (iii), 1.18 (iv))

தீர்வு 

படம்.1.18 (i) மற்றும் படம் 1.18 (iii) வரைபடங்களில், ஒரு குத்துக்கோடு, வரைபடத்தை P மற்றும் Q ஆகிய இரு புள்ளிகளில் வெட்டுவதால் இவை ஒரு சார்பினைக் குறிக்காது.

1.18 (ii) மற்றும் படம்.1.18 (iv) வரைபடங்களில் அதிகபட்சமாக ஒரேயொரு புள்ளியில் வெட்டுவதால், இவை சார்பினைக் குறிக்கும்.

குறிப்பு

ஒரு சமன்பாடு வரைபடத்தில் குறிக்கப்படும்போது அதை வளைவரை எனலாம்.

எடுத்துக்காட்டு 1.11 A = {1, 2, 3, 4} மற்றும் B = {2, 5, 8,11,14} என்பன இரு கணங்கள் என்க. 

f: A→ B எனும் சார்பு f (x) = 3x  − 1 எனக் கொடுக்கப்பட்டுள்ளது. இச்சார்பினைக் கொண்டு 

(i) அம்புக்குறி படம்

(ii) அட்டவணை 

(iii) வரிசைச் சோடிகளின் கணம் 

(iv) வரைபடம் ஆகியவற்றைக் குறிக்க 

தீர்வு

A = {1, 2, 3, 4} ; B = {2, 5, 8,11,14} ;  f (x) = 3x – 1

f (1) = 3(1) – 1 = 3 – 1 = 2 ; f (2) = 3(2) – 1 = 6 – 1 = 5

f (3) = 3(3) – 1 = 9 – 1 = 8 ; f (4) = 4(3) – 1 = 12 – 1 = 11

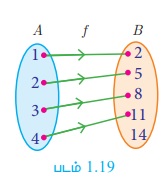
(i) அம்புக்குறி படம்

சார்பு  f : A → B - ஐ அம்புக்குறி படத்தால் குறிப்போம் (படம்.1.19).

(ii) அட்டவணை அமைப்பு

சார்பு f-ஐ கீழேக் கொடுக்கப்பட்டுள்ள அட்டவணையால் குறிப்போம்

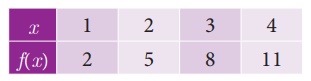
(iii) வரிசைச் சோடிகளின் கணம்

சார்பு f -ஐ வரிசை சோடிகளின் கணமாக எழுதலாம்.

f  = {(1,2), (2,5), (3,8), (4,11)} 

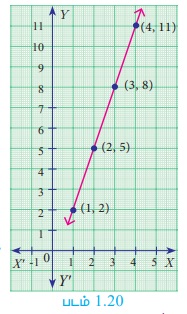
(iv) வரைபடம்

படம் 1.20-ல் உள்ள X Y- தளத்தில் ஒரே நேர்கோட்டில் (1,2), (2,5), (3,8), (4,11) ஆகிய புள்ளிகள் குறிக்கப்பட்டுள்ளன.