கார்டீசியன் பெருக்கல்

கார்டீசியன் பெருக்கல் (Cartesian Product) 

விளக்கம் 1

நாம் பின்வரும் இரண்டு கணங்களை எடுத்துக்கொள்வோம்.

கணம் A-ல் மூன்று காய்கறிகளும் மற்றும் கணம் B-ல் நான்கு பழங்களும் உள்ளன. அதாவது, A = {கேரட் கத்திரிக்காய், வெண்டைக்காய் மற்றும் B = {ஆப்பிள், ஆரஞ்சு, திராட்சை, செம்புற்றுப்பழம்}

ஒரு காயும், ஒரு பழமும் தேர்ந்தெடுப்பதற்குச் சாத்தியமான வழிகள் யாவை? 

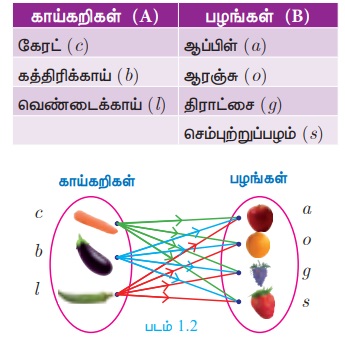
கீழே கொடுக்கப்பட்டுள்ள 12 விதமான சோடிகளின் மூலம் நாம் தேர்வு செய்யலாம். 

{(c, a), (c, o), (c, g), (c, s), (b, a), (b, o), (b, g), (b, s), (l, a), (l, o), (l, g), (l, s)} 

காய்கறிகள் மற்றும் பழங்களின் கார்டீசியன் பெருக்கலை மேற்கண்ட சேகரிப்பு குறிக்கிறது.

வரையறை

A மற்றும் B என்பன இரண்டு வெற்றில்லா கணங்கள் எனில், இவற்றின் வரிசைச் சோடிகளின் கணமானது (a, b) a ∈ A, b ∈ B என இருக்கும். இதை A மற்றும் B -யின் கார்டீசியன் பெருக்கல் என்கிறோம். எனவே, A × B = {(a, b) | a ∈ A, b ∈ B}. A × B என்பதை (A கிராஸ் B) எனப் படிக்கவும். மற்றும் A × Ø = Ø ஆகும்

குறிப்பு 

 • A × B ஆனது, A மற்றும் B என்ற கணங்களுக்கிடையேயான அனைத்து வரிசைச் சோடிகளின் கணம் எனில், அதன் முதல் உறுப்பு A -யின் உறுப்பாகவும், இரண்டாவது உறுப்பு B -யின் உறுப்பாகவும் இருக்கும். 

• B × A ஆனது, A மற்றும் B என்ற கணங்களுக்கிடையேயான அனைத்து வரிசைச் சோடிகளின் கணம் எனில், முதல் உறுப்பு B -யின் உறுப்பாகவும் இரண்டாவது உறுப்பு A -யின் உறுப்பாகவும் இருக்கும். 

• பொதுவாக (a, b) ≠ (b, a). குறிப்பாக, a = b எனில், (a, b) = (b, a)

• கார்டீசியன் பெருக்கலைக் குறுக்கு பெருக்கல் (cross product) எனவும் குறிப்பிடலாம். 

விளக்கம் 2

A = {1, 2, 3} மற்றும் B = {a, b} எனில், A × B மற்றும் B × A-ஐ எழுதுக. 

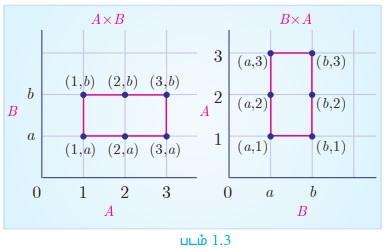
A × B = {1,2,3} × {a, b} = {(1, a), (1, b), (2, a ), (2, b ), (3, a ), (3, b )} (படம் 1.3 -ல் காட்டியுள்ள படி) 

B×A = {a, b} × {1,2,3} = {(a,1), (a,2), (a,3), (b,1), (b,2), (b,3)} (படம் 1.3-ல் காட்டியுள்ளபடி)

சிந்தனைக் களம் 

எப்போது A× B ஆனது B × A விற்கு சமம்? 

குறிப்பு 

• பொதுவாக A× B ≠ B × A, ஆனால் n(A× B) = n(B × A) 

• A× B = Ø எனில், A = Ø அல்லது B = Ø

• n(A) = p மற்றும் n(B) = q எனில், n(A× B) = p q

நிலையான முடிவற்ற கணங்களுக்கான மீள் பார்வை

இயல் எண்கள் N = {1,2,3,4...}; முழு எண்கள் W = {0,1,2,3, ...};

முழுக்கள் Z = {..., -2,-1,0,1,2, ...}; விகிதமுறு எண்கள்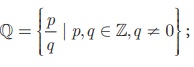

மெய் எண்கள் R =  Q  ∪ Q’, இங்கு Q’ -ஆனது விகிதமுறா எண்களின் கணமாகும்.

விளக்கம் 3

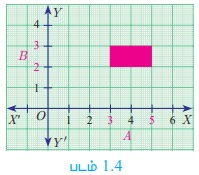
A என்ற கணமானது, [3, 5] என்ற இடைவெளியில் உள்ள அனைத்து எண்கள் மற்றும் B என்ற கணமானது, [2, 3] என்ற இடைவெளியில் உள்ள அனைத்து எண்கள் எனில், A × B -யின் கார்டீசியன் பெருக்கல் ஆனது படம் 1.4 -ல் காண்பது போலச் செவ்வகப் பகுதியைக் குறிக்கும். A × B என்ற கணத்தின் (x, y) என்ற புள்ளிகள் செவ்வகப் பகுதியில் அமைந்திருக்கும்.

முன்னேற்றச் சோதனை 

1. A மற்றும் B ஆகியன ஏதேனும் இரண்டு வெற்றில்லா கணங்கள் எனில், A × B –ஐ ___________ எனலாம். 

2. n(A × B) = 20 மற்றும் n( A) = 5 எனில், n( B) ஆனது _____________ 

3. A = {-1,1} மற்றும் B = {-1,1} எனில், வடிவியல் முறையில் A × B கணத்தின் புள்ளிகள் யாவை? 

4. A, B என்பவை முறையே (-4, 3] மற்றும் (-2, 3) -க்கு இடைவெளியில் உள்ள அனைத்து எண்கள் எனில், A மற்றும் B -ன் கார்டீசியன் பெருக்கலைக் குறிப்பிடுக.

குறிப்பு 

கார்டீசியன் தளத்தில் உள்ள அனைத்துப் புள்ளிகளின் கணத்தை (x, y) என்ற வரிசைச் சோடிகளின் கணமாக அறியலாம். இதில் x, y ஆகியவை மெய்யெண்கள். ℝ×ℝ என்ற கணத்தில் உள்ள அனைத்துப் புள்ளிகளையும் சேர்த்து நாம் கார்டீசியன் தளம் என அழைக்கிறோம்.

செயல்பாடு 1 

A = {x | x ∈ N, x ≤ 4}, B = {y | y ∈ N, y < 3} எனில் A × B மற்றும் B× A -ஐ வரைபடத்தாளில் குறிக்க A × B மற்றும் B × A -க்கு உள்ள வேறுபாட்டை உங்களால் காணமுடிகிறதா? 

எடுத்துக்காட்டு 1.1 A = {1,3,5}, B = {2,3} எனில் (i) A × B மற்றும் B × A -ஐ காண்க. 

(ii) A × B = B × A ஆகுமா? இல்லையெனில் ஏன்?  

(iii) n(A×B) = n(B×A) = n(A)× n(B) எனக் காட்டுக. 

தீர்வு A = {1,3,5} , B = {2,3} எனக் கொடுக்கப்பட்டுள்ளன.

(i) A×B = {1,3,5} × {2,3} = {(1,2), (1,3), (3,2), (3,3), (5,2), (5,3)} ...(1)

B× A = {2,3} × {1,3,5} = {(2,1), (2,3), (2,5), (3,1), (3,3), (3,5)} ...(2)

(ii) (1) மற்றும் (2) -ன் மூலமாக A × B ≠ B ×A ஏனெனில் (1,2) ≠ (2,1), (1,3) ≠ (3,1)... 

(iii) n(A)=3; n (B) = 2. 

(1) மற்றும் (2) -லிருந்து நாம் காண்பது, n (A×B) = n (B×A) = 6;

n (A) ×n (B) = 3 × 2 = 6 மற்றும் n (B) × n (A) = 2 × 3 = 6 

எனவே, n (A×B) =n (B×A) = n(A) × n (B) = 6. 

ஆகவே, n (A×B) =n (B×A) = n(A) × n (B).

எடுத்துக்காட்டு 1.2 

If A×B = {(3,2), (3,4), (5,2), (5,4)} எனில் A மற்றும் B -ஐ காண்க.

தீர்வு A×B ={(3,2), (3,4), (5,2), (5,4)}

A = {A×B -யின் முதல் ஆயத்தொலைவு உறுப்புகளின் கணம்}. எனவே, A = {3,5} 

B = {A×B -யின் இரண்டாம் ஆயத்தொலைவு உறுப்புகளின் கணம்}. எனவே, B = {2,4}

எனவே A = {3,5} மற்றும் B = {2,4}. 

எடுத்துக்காட்டு 1.3 A = {x ∈ N | 1 < x <4}, B = {x ∈ W| 0 ≤ x < 2} மற்றும் C = {x ∈ N | x<3} . என்க.

(i) A × (B U C) = (A × B) U (A × C)

(ii) A × (B Ո C) = (A × B) Ո (A × C) என்பனவற்றைச் சரிபார்க்க. 

தீர்வு 

A = {x ∈ N| 1 < x < 4} = {2, 3} , B = {x ∈W | 0 ≤ x < 2} = {0, 1},

C = {x ∈ N | x < 3}= {1,2}

(i) A × (B ∪ C)  = (A × B ) ∪ (A × C)

B ∪ C  = {0, 1} ∪ {1, 2} = {0, 1, 2}

A × (B ∪C) = {2, 3} × {0, 1, 2} = {(2, 0), (2, 1), (2, 2), (3, 0), (3, 1), (3, 2)}    ...(1)

A × B = {2, 3} × {0, 1} = {(2,0),(2,1),(3,0),(3,1)}

A × C = {2, 3} × {1, 2} = {(2, 1), (2, 2), (3, 1), (3, 2)}

(A × B) ∪ (A ×C) = {(2, 0), (2, 1), (3, 0), (3, 1)} ∪ {(2, 1), (2, 2), (3, 1), (3, 2)}

= {(2, 0), (2, 1), (2, 2), (3, 0), (3, 1), (3, 2)} ...(2)

(1) மற்றும் (2) -லிருந்து, A × (B ∪C ) = (A×B ) ∪ (A×C) என்பது சரிபார்க்கப்பட்டது 

(ii) A × (B ∩C)  = (A ×B) ∩ (A ×C)

B Ո C = {0, 1} ∩ {1, 2} = {1}

A × (B ∩C) = {2, 3} ×{1} = {(2,1),(3,1)} ... (3)

A × B = {2, 3} ×{0, 1} = {(2, 0),(2, 1),(3, 0),(3, 1)}

A × C = {2, 3} ×{1, 2} = {(2, 1),(2, 2),(3, 1),(3, 2)}

(A × B) ∩ (A × C) = {(2, 0),(2, 1),(3, 0),(3, 1)} ∩ {(2, 1),(2, 2),(3, 1),(3, 2)}

= {(2, 1), (3, 1)} ... (4)

(3) மற்றும் (4), A × (B ∩ C) = (A × B) ∩ (A × C) என்பது சரிபார்க்கப்பட்டது.

குறிப்பு

மேலே, சரிபார்க்கப்பட்ட சமன்பாடுகள் முறையே கார்டீசியன் பெருக்கலின் சேர்ப்பு மற்றும் வெட்டுகளின் மீதான பங்கீட்டு பண்புகளாகும். A, B மற்றும் C என்பன ஏதேனும் மூன்று கணங்கள் எனில்

(i) A × (B ∪ C) = (A × B) ∪ (A × C) (ii) A × (B ∩ C) = (A×B) ∩ (A×C).

மூன்று கணங்களின் கார்டீசியன் பெருக்கல் (Cartesian Product of three Sets)

A, B, C ஆகியவை வெற்றில்லா கணங்கள் எனில், அதன் கார்டீசியன் பெருக்கற்பலனின் கணமானது அனைத்து சாத்தியமான வரிசையில் அமைந்த மூன்றின் தொகுதிகளின் கணமாகும்.

A × B × C = {(a, b, c) அனைத்து a ∈ A, b ∈ B, c ∈ C}

இரண்டு மற்றும் மூன்று கணங்களுக்கான கார்டீசியன் பெருக்கலின் வடிவியல் விளக்கம் 

A = {0, 1}, B = {0, 1}, C = {0, 1} என்க

A × B = {0, 1} × {0, 1} = {(0, 0), (0,1), (1, 0), (1,1)}

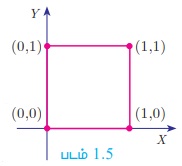
A × B ஆனது XY- தளத்தில் (plane) குறிக்கப்பட்டுள்ளதைப் படம் 1.5-ல் காணலாம்.

(A × B) × C = {(0, 0), (0,1), (1, 0), (1,1)} × {0,1}

= {(0, 0, 0), (0, 0,1), (0,1, 0), (0,1,1), (1, 0, 0), (1, 0,1) (1,1, 0), (1,1,1)}

A × B × C ஆனது XYZ - என்ற வெளியில் (space) குறிக்கப்பட்டுள்ளதைப் படம் 1.6 ல் காணலாம்.

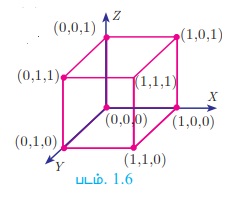
A × B என்பது இரு பரிமாணத்தில் சதுரத்தின் புள்ளிகளைக் குறிக்கிறது. A × B × C என்பது முப்பரிமாணத்தில் கனசதுரத்தின் புள்ளிகளைக் குறிக்கிறது.

குறிப்பு 

பொதுவாக, இரண்டு வெற்றில்லா கணங்களின் கார்டீசியன் பெருக்கல் இரு பரிமாணங்களைக் கொண்ட வடிவத்தை ஏற்படுத்தும். அதேபோல் மூன்று வெற்றில்லா கணங்களின் கார்டீசியன் பெருக்கல் மூன்று பரிமாணங்களைக் கொண்ட முப்பரிமாணப் பொருளை ஏற்படுத்தும்.