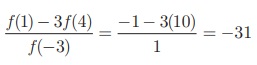சார்புகளின் சிறப்பு வகைகள்

சார்புகளின் சிறப்பு வகைகள் (Special cases of function)

சில சிறப்பு வகையான சார்புகள் மிகவும் பயனுள்ளதாக இருக்கும். அவற்றுள் சில கீழே கொடுக்கப்பட்டுள்ளன.

(i) மாறிலிச் சார்பு 

(ii) சமனிச் சார்பு 

(iii) மெய் மதிப்புச் சார்பு 

(i) மாறிலிச் சார்பு (Constant function)

சார்பு f : A → B ஆனது மாறிலிச் சார்பு எனில், f -ன் வீச்சகமானது ஒரே ஓர் உறுப்பைக் கொண்டதாகும். அதாவது, f (x) = c,  x ∈ A மற்றும் ஏதேனும் ஒரு நிலையான c ∈ B. 

விளக்கம் 16

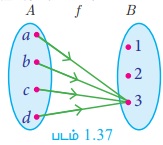
படம் 1.37-லிருந்து, A = {a, b, c, d}, B = {1, 2, 3} மற்றும் f = {( a,3), (b, 3), (c,3), (d, 3)} இதை, f(x) = 3 ∀ x ∈ A  என எழுதலாம். மேலும், f - யின் வீச்சகம் f = {3} எனவே f -ஆனது மாறிலிச் சார்பு ஆகும்.

(ii) சமனிச் சார்பு (Identity function)

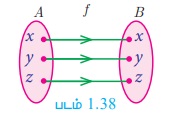
A ஒரு வெற்றில்லா கணம் என்க. சார்பு f: A → A ஆனது f(x) = x அனைத்து x ∈ A என வரையறுக்கப்பட்டால், அந்தச் சார்பு A-யின் சமனிச் சார்பு எனப்படும். இதை IA எனக் குறிக்கலாம். 

விளக்கம் 17

A = {a,b,c} எனில்  f = IA = {(a,a), (b,b), (c,c)} ஆனது A-யின் மீதான சமனிச் சார்பாகும் 

(iii) மெய் மதிப்புச் சார்பு (Real - valued function)

சார்பு f: A → B ஆனது மெய் மதிப்புச் சார்பு எனில், f-யின் வீச்சகமானது, R எனும் மெய்யெண்களின் உட்கணமாக இருக்கும். அதாவது, f (a) ⊆ R, இங்கு ∀ f (a) ⊆ R ஆகும்.

சிந்தனைக் களம்

சமனிச் சார்பு ஒன்றுக்கு ஒன்றான சார்பாகுமா? 

முன்னேற்றச் சோதனை

சரியா அல்லது தவறா? 

1. எல்லா ஒன்றுக்கு ஒன்று சார்புகளும் மேல் சார்பாகும். 

2. n(A) = 4, n(B) = 3 ஆக இருக்கும்போது A-லிருந்து B க்கு அமையும் சார்பு ஒன்றுக்கொன்றாக இருக்காது. 

3. எல்லா மேல்சார்புகளும் ஒன்றுக்கு ஒன்றான சார்புகளாகும். 

4. n(A) = 4, n(B) = 5 ஆக இருக்கும்போது A-யிலிருந்து B-க்கான சார்பு மேல் சார்பாக இருக்க முடியாது. 

5. A-லிருந்து B-க்கான சார்பு f ஆனது, ஓர் இருபுறச் சார்பு எனில், n(A) = n(B)

6. n(A) = n(B) எனில் f ஆனது, A-யிலிருந்து B-க்கு ஓர் இருபுறச்சார்பு. 

7. எல்லா மாறிலிச் சார்புகளும் இருபுறச் சார்புகளாகும்.

எடுத்துக்காட்டு 1.17

f ஆனது R-லிருந்து R-க்கு ஆன சார்பு. மேலும் அது f (x) = 3x − 5 என வரையறுக்கப்படுகிறது. (a, 4) மற்றும் (1, b) எனக் கொடுக்கப்பட்டால் a மற்றும் b -யின் மதிப்புகளைக் காண்க. 

தீர்வு f (x) = 3x − 5, f   = {(x, 3x – 5) | x ∈ R} என எழுதலாம். 

(a, 4) எனில், a-யின் நிழல் உரு 4. அதாவது, f (a)  = 4

3a – 5 = 4 -லிருந்து a = 3 

(1, b) எனில், 1 -யின் நிழல் உரு b. அதாவது, f (1) = b 

3(1) - 5 = b எனவே, b = -2

எடுத்துக்காட்டு 1.18 

சார்பு f: R → R ஆனது 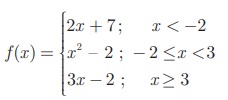என வரையறுக்கப்பட்டால்,

(i) f (4)

(ii) f (-2)

(iii) f (4) + 2f (1)

(iv) [f (1) - 3f (4)] / f (-3)

ஆகியவற்றின் மதிப்புகளைக் காண்க

தீர்வு

அருகில் காட்டியுள்ளபடி சார்பு f ஆனது I, II, III 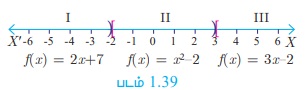என்ற மூன்று இடைவெளிகளில் வரையறுக்கப்படுகிறது.

x = a என்ற கொடுக்கப்பட்ட மதிப்பிற்கு a-இருக்கும் இடைவெளியைக் கண்டுபிடித்து, அந்த இடைவெளியில் f(a) -ஐக் காண வேண்டும். 

(i) x = 4 ஆனது மூன்றாவது இடைவெளியில் உள்ளதை நாம் காணலாம்.

இங்கு, f(x) = 3x − 2; f (4) = 3(4) – 2 = 10 

(ii) x = −2 ஆனது இரண்டாவது இடைவெளியில் உள்ளது.

எனவே, f (x) = x2 – 2; f (−2) = (−2)2 – 2 = 2 

(iii) (i) - லிருந்து, f (4) = 10.

f(1) - ன் மதிப்பைக் காண, x = 1 ஆனது இரண்டாவது இடைவெளியில் உள்ளது. 

ஆகையினால், f (x) = x2 – 2 -லிருந்து, f (1) = 12 – 2 = −1

எனவே,  f (4) + 2f (1) = 10 + 2(−1) = 8

(iv) f (1) = -1,  f (4) = 10 எனக் கண்டோம். f (-3) -யைக் காண x  = −3 ஆனது ஒன்றாவது இடைவெளியில் உள்ளதைக் காணலாம். 

ஆகையினால், f (x) = 2x + 7; எனவே, f (−3) = 2(−3) + 7 = 1

எனவே,