பயிற்சி 1.5 : சார்புகளின் சேர்ப்பு

பயிற்சி 1.5 

1. கீழேக் கொடுக்கப்பட்டுள்ள f மற்றும் g எனும் சார்புகளைப் பயன்படுத்தி f o g மற்றும் g o f -ஐக் காண்க. f o g = g o f என்பது சரியா சோதிக்க. 

(i) f (x) = x − 6, g(x) = x2

(ii) f (x) = 2/x, g(x) = 2x2 – 1

(iii) f (x) = 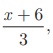 g(x) = 3 – x

(iv) f (x) = 3 + x, g(x) = x – 4

(v) f (x) = 4x2 − 1, g(x) = 1 + x

2. f o g = g o f எனில் k-யின் மதிப்பைக் காண்க.

(i) f (x) = 3x + 2, g(x) = 6x – k

(ii) f (x) = 2x − k, g(x) = 4x + 5

3. f (x) = 2x − 1, g(x) = [x+1]/2 எனில், f o g = g o f = x எனக் காட்டுக. 

4. f (x) = x2 − 1, g(x) = x − 2 மற்றும் g o f (a) = 1 எனில், a-ஐக் காண்க.

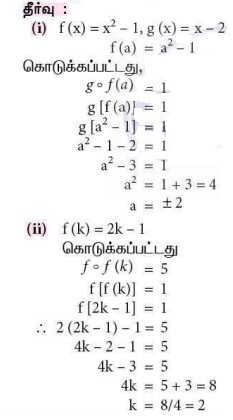
5. A, B, C ⊆ N மற்றும் f : A → B என்ற சார்பு f (x) = 2x + 1 எனவும் மற்றும் g : B → C ஆனது g(x) = x2  எனவும் வரையறுக்கப்பட்டால், f o g மற்றும் g o f . -யின் வீச்சகத்தைக் காண்க. 

6. f (x) = x2 − 1 எனில் (i) f o f (ii) f o f o f -ஐக் காண்க. 

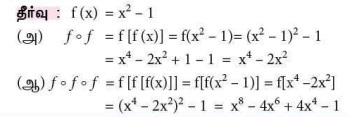
7. f : R → R மற்றும் g : R → R ஆனது முறையே, f (x) = x5 , g(x) = x4 என வரையறுக்கப்பட்டால், f, g ஆகியவை ஒன்றுக்கு ஒன்றானதா மற்றும் f o g ஒன்றுக்கு ஒன்றான சார்பாகுமா என்று ஆராய்க. 

8. கொடுக்கப்பட்ட f (x), g(x), h(x) ஆகியவற்றைக் கொண்டு (f o g) o h = f o (g o h) எனக் காட்டுக.

(i) f (x) = x − 1, g(x) = 3x + 1 மற்றும் h(x) = x2

(ii) f (x) = x2, g(x) = 2x மற்றும் h(x) = x + 4

(iii) f (x) = x − 4, g(x) = x2 மற்றும் h(x) = 3x – 5

9. f = {(−1, 3), (0, −1), (2, −9)} ஆனது Z - லிருந்து Z -க்கான ஒரு நேரிய சார்பு எனில், f (x) -ஐக் காண்க. 

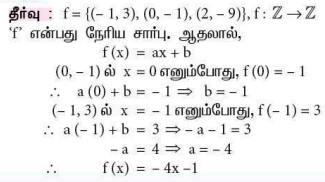
10. ஒரு மின்சுற்றுக் கோட்பாட்டின்படி, C(t) என்ற ஒரு நேரிய சுற்று, C (at1 + bt2 ) = aC (t1) + bC(t2), –ஐ பூர்த்தி செய்கிறது. மேலும் இங்கு a, b ஆகியவை மாறிலிகள் எனில், C (t) = 3t ஆனது ஒரு நேரிய சுற்று எனக் காட்டுக.

விடைகள்: