வரையறை, விளக்கம், எடுத்துக்காட்டு, தீர்வு | கணக்கு - உறவுகள் | 10th Mathematics : UNIT 1 : Relation and Function
10வது கணக்கு : அலகு 1 : உறவுகளும் சார்புகளும்
உறவுகள்
உறவுகள் (Relations)
நம் அன்றாட வாழ்வில் இரு பொருள்கள் சில விதிகளுக்குட்பட்டு ஒன்றுக்கொன்று தொடர்பில் இருப்பதை நாம் காண்கிறோம். அந்த இரண்டு பொருள்களும் ஒரு சில விதிகளுக்குட்பட்டு அத்தொடர்பை ஏற்படுத்துகின்றன. அவ்வாறெனில், அத்தொடர்பை எப்படி வெளிப்படுத்தலாம்? இங்குச் சில எடுத்துக்காட்டுகள் கொடுக்கப்பட்டுள்ளன.
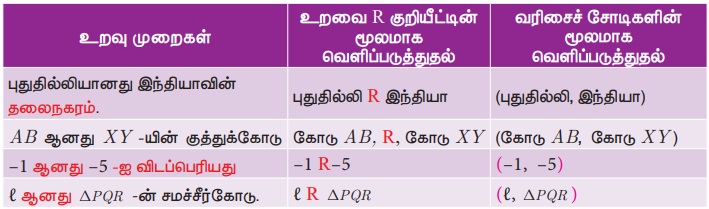
எப்படி புதுதில்லியும் இந்தியாவும் தொடர்புடையன? நாம் பதிலை எதிர்நோக்குகிறோம். புதுதில்லியானது இந்தியாவின் தலைநகரம். ஆனால் புதுதில்லியையும் இந்தியாவையும் பல வழிகளில் தொடர்புபடுத்தலாம். ஒரு சில வழிகள் பின்வருமாறு.
• புதுதில்லியானது இந்தியாவின் தலைநகரம்.
• புதுதில்லியானது இந்தியாவின் வடபகுதியில் உள்ளது.
• புதுதில்லியானது இந்தியாவின் மிகப்பெரிய நகரங்களில் ஒன்று.
நாம் உறவுகளை மிகச் சரியாகக் குறிப்பிட வேண்டுமெனில், ஒரே ஓர் வரிசைச்சோடி (புதுதில்லி, இந்தியா) மட்டும் கொடுத்தால் போதுமானதாக இருக்காது. மேற்கண்ட மூன்று குறிப்புகளும் அதற்குப் பொருந்தும். எனவே, கொடுக்கப்பட்ட வரிசைச் சோடிகளில் எந்த உறவுமுறை கொடுக்கப்பட்டுள்ளது என நாம் கேட்க நினைத்தால், உறவைக் குறிப்பிடுவது எளிதாக இருக்கும்.
{(புதுதில்லி, இந்தியா), (வாஷிங்டன், அமெரிக்க ஐக்கிய நாடுகள்), (பெய்சிங், சீனா), (லண்டன், இங்கிலாந்து), (காத்மாண்டு, நேபாளம்)} என்ற வரிசைச் சோடிகளில் காணப்படும் உறவை எளிதாக வெளிப்படுத்த முடியும் அல்லவா?
விளக்கம் 4

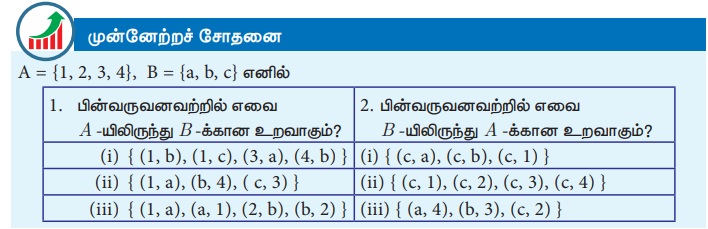
உயரத்திற்கும் மாணவருக்கும் இடையிலான உறவை நாம் வரையறுக்கலாம். (படம்.1.7)
R = {(உயரம், மாணவர்)}
R = {(4.5, S1), (4.5, S4), (4.7, S9), (4.9, S10), (5, S3), (5, S5), (5, S8), (5.1, S6), (5.2, S2), (5.2, S7)}
வரையறை
A மற்றும் B என்பன இரண்டு வெற்றில்லா கணங்கள் என்க. A -யிலிருந்து B-க்கு உள்ள உறவு R ஆனது சில விதிமுறைகளை நிறைவு செய்து, A × B -யின் உட்கணமாக இருக்கும். x ∈ A -விற்கும் y ∈ B -க்குமான உறவு R -யின் வழியாக இருந்தால் x Ry என எழுதலாம். x Ry என இருந்தால், இருந்தால் மட்டும் (x, y) ∈ R.
உறவு R-யின் மதிப்பகம் = {x ∈ A | x R y, ஏதேனும் ஒரு y ∈ B}
உறவு R-ன் துணை மதிப்பகம் = B ஆகும்.
உறவு R-ன் வீச்சகம் = {y ∈ B | x Ry, ஏதேனும் ஒரு x ∈ A}
இந்த வரையறைகளிலிருந்து, R -யின் மதிப்பகமானது ⊆ A, R-ன் துணை மதிப்பகம் = B மற்றும் R -யின் வீச்சகம் ⊆ B என்பதைக் காணலாம்.
விளக்கம் 5
A = {1,2,3,4,5}, B = {மதி, அருள், ஜான்} என்க.
மேற்கண்ட A மற்றும் B கணங்களின் உறவு R-ஐ அம்புக்குறிப் படத்தில் குறிக்கலாம். (படம் 1.8)
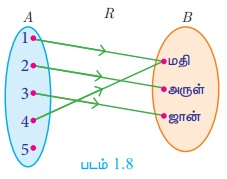
எனவே R-யின் மதிப்பகம் = {1,2,3,4}
R-யின் வீச்சகம் = {மதி, அருள், ஜான்}
R-யின் மதிப்பகமானது, A-யின் தகு உட்கணமாவதைக் காண்க
செயல்பாடு 2
A மற்றும் B ஆனது xy -தளத்திலுள்ள கோடுகளின் கணங்கள் என்க. A-யில் x- அச்சுக்கு இணையான கோடுகள் உள்ளன. x ∈ A, y ∈ B என்க. மேலும், x Ry எனில், x ஆனது y -க்கு செங்குத்துக் கோடு எனக் கருதுக. வரைபடத்தைப் பயன்படுத்தி B -யின் உறுப்புகளைக் காண்க.
விளக்கம் 6
A = {1,3,5,7} மற்றும் B = {4,8} என்க. A-லிருந்து B-க்கு R என்ற உறவானது ‘குறைவாக உள்ளது’ என வரையறுக்கப்பட்டால், 1R4 என எழுதலாம். (1 ஆனது 4-ஐ விடக் குறைவானது). அதைப்போலவே, 1R8, 3R4, 3R8, 5R8, 7R8
அதாவது, R = {(1,4), (1,8), (3,4), (3,8), (5,8), (7,8)}
குறிப்பு
மேற்கண்ட விளக்கத்தில், A×B = {(1,4), (1,8), (3,4), (3,8), (5,4), (5,8), (7,4), (7,8)}
R = {(1,4), (1,8), (3,4), (3,8), (5,8), (7,8)} R ஆனது A × B -ன் உட்கணமாக இருப்பதைக் காணலாம்.
விளக்கம் 7
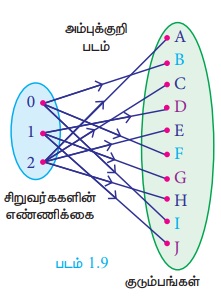
ஒரு நகரத்தில் குறிப்பிட்ட பகுதியில் இரண்டு குழந்தைகள் உள்ள பத்துக் குடும்பங்கள் A, B, C, D, E, F, G, H, I மற்றும் J எனக் கருதிக் கொள்வோம். இவற்றில் B, F, I குடும்பங்களில் இரண்டு சிறுமிகளும் D, G, J -யில் ஒரு சிறுவன் மற்றும் ஒரு சிறுமியும், மீதமுள்ள குடும்பங்களில் இரண்டு சிறுவர்களும் உள்ளனர். நாம் உறவு R-ஐ, xRy என வரையறுக்கலாம். இங்கு x-ஆனது சிறுவர்களின் எண்ணிக்கையையும், மற்றும் y -ஆனது x எண்ணிக்கையை கொண்ட சிறுவர்கள் உள்ள குடும்பத்தையும் குறிக்கின்றது. இந்த நிலைமையை ஓர் உறவாகக் கொண்டு வரிசைச்சோடிகள் மற்றும் அம்புக்குறி படங்கள் வழியாகக் குறிப்பிடுக.
உறவு R -யின் மதிப்பகம் இரு குழந்தைகள் கொண்ட சிறுவர்களின் எண்ணிக்கையைக் குறிக்கிறது. எனவே, R -யின் மதிப்பகம் = {0,1,2} ஆகிய மூன்று உறுப்புகளைக் கொண்டிருக்கும். இங்கு 0 சிறுவர் உள்ள குடும்பங்களே, இரண்டு சிறுமிகளைக் கொண்ட குடும்பங்களாகும். 1 சிறுவர் கொண்ட குடும்பங்களில் 1 சிறுவனும், 1 சிறுமியும் இருப்பார்கள். எனவே, R என்ற உறவானது பின்வருமாறு:
R = {(0, B), (0, F), (0, I), (1, D), (1, G), (1, J), (2, A), (2,C ), (2, E), (2, H )}
இந்த உறவு அம்புக்குறி படத்தில் (படம் 1.9) காட்டப்பட்டுள்ளது.
எடுத்துக்காட்டு 1.4
A = {3,4,7,8} மற்றும் B = {1,7,10} எனில் கீழ் உள்ள கணங்களில் எவை A-லிருந்து B-க்கு ஆன உறவைக் குறிக்கின்றது?
(i) R1 = {(3,7), (4,7), (7,10), (8,1)}
(ii) R2 = {(3,1), (4,12)}
(iii) R3 = {(3,7), (4,10), (7,7), (7,8), (8,11), (8,7), (8,10)}
தீர்வு A × B = {(3,1), (3,7), (3,10), (4,1), (4,7), (4,10), (7,1), (7,7), (7,10), (8,1), (8,7), (8,10)}
(i) R1 ⊆ A × B என்பதைக் காணலாம். எனவே, R1 என்பது A -லிருந்து B-க்கு ஆன உறவு ஆகும்.
(ii) இங்கு, (4,12) ∈ R2, ஆனால் (4,12) ∉ A × B. எனவே, R2 ஆனது A -லிருந்து B-க்கு ஆன உறவு இல்லை.
(iii) இங்கு, (7, 8) ∈ R3, ஆனால் (7, 8) ∉ A × B. எனவே, R3 ஆனது A -லிருந்து B-க்கு ஆன உறவு இல்லை.
குறிப்பு
• ஓர் உறவை, பட்டியல் முறையிலோ அல்லது கணக் கட்டமைப்பு முறையிலோ குறிக்கலாம்.
• உறவைக் காட்சிப்படுத்தி அறிய அம்புக்குறி படத்தைப் பயன்படுத்தலாம்.
எடுத்துக்காட்டு 1.5
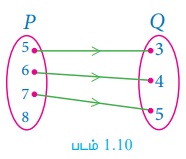
படத்தில் காட்டப்பட்டுள்ள (படம் 1.10) அம்புக்குறி படமானது P மற்றும் Q கணங்களுக்கான உறவைக் குறிக்கின்றது. இந்த உறவை (i) கணகட்டமைப்பு முறை, (ii) பட்டியல் முறைகளில் எழுதுக. (iii) R -ன் மதிப்பகம் மற்றும் வீச்சகத்தைக் காண்க.
தீர்வு
(i) R யின் கணகட்டமைப்பு முறை {(x, y) | y = x − 2, x ∈ P, y ∈ Q}
(ii) R யின் பட்டியல் முறை = {(5,3), (6,4), (7,5)}
(iii) R யின் மதிப்பகம் = {5,6,7}; R யின் வீச்சகம் = {3,4,5}
‘இன்மை உறவு' (Null relation)
பின்வரும் எடுத்துக்காட்டைக் கருதுவோம்.
A = {-3, -2, -1} மற்றும் B = {1,2,3,4} எனில், A -லிருந்து B -க்கான உறவை a - b = 8, a∈A, b∈B, என வரையறுத்தால், a - b = 8 என்றவாறு எந்தவொரு (a, b) சோடியும் இல்லை. எனவே, R-ல் எந்த உறுப்பும் இல்லை. அப்படியானால் R = ɸ ,
ஓர் உறவில் உறுப்புகள் இல்லை என்றால் அது இன்மை உறவு எனப்படும்..
உங்களுக்குத் தெரியுமா?
n(A) = p, n(B) = q, எனில், A யிலிருந்து B-க்கு கிடைக்கும் மொத்த உறவுகளின் எண்ணிக்கையானது 2pq ஆகும்.