புவியின் ஈர்ப்பு முடுக்கம்

புவியின் ஈர்ப்பு முடுக்கம்

பொருள்கள் புவியின் மீது விழும்போது, அவை புவியினை நோக்கி முடுக்கமடைவதை காண்கிறோம். நியூட்டன் இரண்டாம் விதிப்படி புறவிசை செயல்பட்டால் மட்டுமே ஒரு பொருள் முடுக்கமடையும் என அறிவோம். இங்கு புவியின் ஈர்ப்பு விசையால் பொருள்கள் முடுக்கமடைகின்றன. புவியின் அருகே இவ்விசை அனைத்து பொருள்கள் மீதும் மாறாத முடுக்கத்தை ஏற்படுகிறது. மேலும் இம்முடுக்கமானது பொருள்களின் நிறைகளை சார்ந்தது அல்ல. புவி பரப்புக்கு அருகே உள்ள நிறை மீது புவியினால் ஏற்படும் ஈர்ப்பு விசை

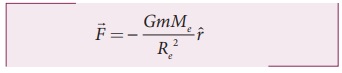
இந்த ஈர்ப்பு விசையை நியுட்டனின் இரண்டாம் விதியுடன் சமப்படுத்த

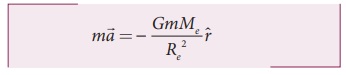
எனவே, முடுக்கம்

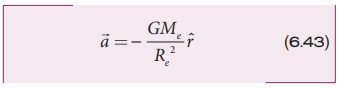
புவிப் பரப்புக்கு அருகே உள்ள பொருளுக்கு புவியின் ஈர்ப்பு புலத்தால் ஏற்படும் முடுக்கமானது, ஈர்ப்பு முடுக்கம் எனப்படுகிறது. இது g என்ற குறியீட்டால் குறிக்கப்படுகிறது.

ஈர்ப்பு முடுக்கத்தின் எண் மதிப்பு

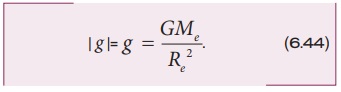
இச்சமன்பாட்டிலிருந்து ஈர்ப்பின் முடுக்கமானது முடுக்கமடையும் பொருளின் நிறையை சார்ந்ததல்ல என அறிகின்றோம்.  g ன் மதிப்பானது புவியின் நிறையையும் ஆரத்தையும் சார்ந்துள்ளது. ‘’புவியினை நோக்கி விழும் அனைத்து பொருள்களும் சமமாக முடுக்கமடைகிறது’’ என்பதை கலிலியோ 400 ஆண்டுகளுக்கு முன்பே பல ஆய்வுகள் மூலம் கண்டறிந்தார். 

புவியின் பூமத்திய ரேகை பகுதியில் ஈர்ப்பின் முடுக்கம் g = 9.8 ms-2 என கண்டறியப்பட்டுள்ளது.

குத்துயரம், ஆழம் மற்றும் குறுக்குக்கோடு ஆகியவற்றைச் சார்ந்து ஈர்ப்பின் முடுக்கம் மாறுபடுதல்

புவிபரப்பிலிருந்து h உயரத்தில் உள்ள நிறை m ஐ கருதுவோம். புவியின் ஈர்ப்பு விசையால் அப்பொருள் உணரும் முடுக்கம்

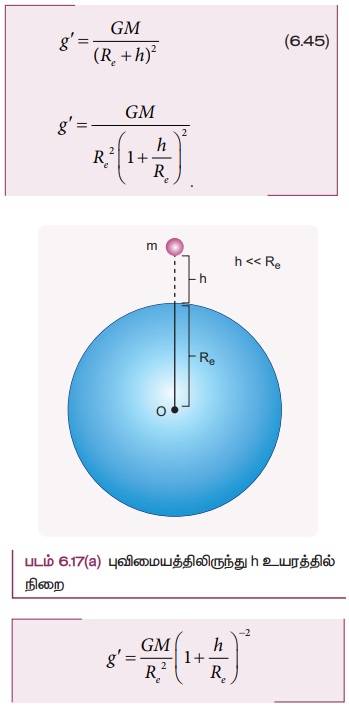
h << Re எனில் ஈருறுப்பு தேற்றத்தினை பயன்படுத்தி பின்பு உயர் அடுக்குகளைப் புறக்கணித்துப் பின்வருமாறு எழுதலாம்.

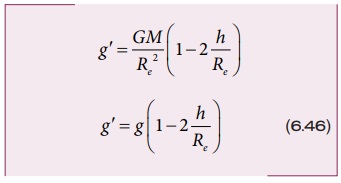
இதிலிருந்து g'<g என நாம் காண்கிறோம். இதன் பொருள் குத்துயரம் h அதிகரிக்கும் போது ஈர்ப்பு முடுக்கம் g குறைகிறது என்பதாகும்.

எடுத்துக்காட்டு 6.7

(அ) 15 மீட்டர் உயரத்திலிருந்து 1/2 kg நிறையுடைய மாம்பழம் கீழே விழுகிறது. கீழே விழத் தொடங்கும் போது அதன் ஈர்ப்பின் முடுக்கம் யாது? (g = 9.8 m s-2; புவியின் ஆரம் = 6400 × 103 m)

தீர்வு:

(ஆ) புவி பரப்பிலிருந்து 1600 km உயரத்தில் ஒரு துணைக்கோள் புவியை சுற்றி வருகின்றது. புவியின் ஈர்ப்பு விசையால் துணைக்கோள் அடையும் முடுக்கம் யாது?

தீர்வு

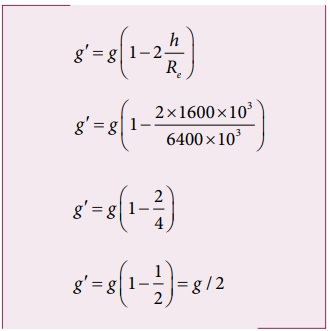
இந்த இரு எடுத்துக்காட்டுகள் மூலம் புவிக்கு அருகே ஈர்ப்பின் முடுக்கம் மாறிலியாக உள்ளது எனத்தெரிகிறது.

சிந்தனைக்கு

h=Re என்று சமன்பாடு 6.46-ல் பிரதியிட்டு கணக்கீடு செய்யலாமா? செய்யமுடியாது ஏனென்றால் h<<Re என்ற நியதியின் அடிப்படையிலேயே 6.46 சமன்பாட்டை நாம் பெற்றுள்ளோம். h=Re எனும்போது நாம் சமன்பாடு 6.45 ஐ பயன்படுத்த வேண்டும்.

ஆழத்தைப் பொறுத்து g மாறுபடுதல் 

புவியின் ஆழ் சுரங்கம் ஒன்றில் உதாரணமாக, (நெய்வேலி நிலக்கரிச் சுரங்கம்) d ஆழத்தில் நிறை m உள்ளது என்க.

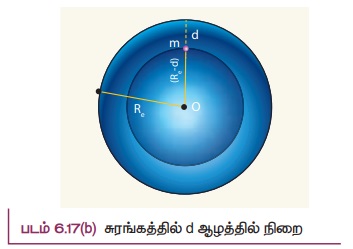
சுரங்கத்தின் ஆழம் d என்க. d ஆழத்தில் g' மதிப்பை கணக்கிட கீழ்க்கண்ட கருத்துகளை கவனத்தில் கொள்வோம். நிறை அடையும் முடுக்கத்தில் புவியின் (Re - d) க்கு மேலே உள்ள புவியின் பகுதியானது இந்த முடுக்கத்திற்கு ஏதும் பங்களிப்பு செய்வதில்லை. முந்தைய பகுதியில் நிரூபிக்கப்பட்ட முடிவின்படி 

d ஆழத்தில் ஈர்ப்பின் முடுக்கம்

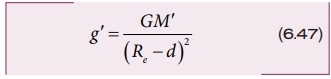
(Re - d) உடைய புவி பகுதியின் நிறை M' ஆகும். புவியின் அடர்த்தி ρ சீராக அனைத்து பகுதியிலும் சீராக (uniform) உள்ளது எனக் கருதினோம் எனில்,

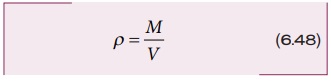
இங்கு M - புவியின் நிறை மற்றும்

V- புவியின் பருமன் ஆகும் 

மேலும் அடர்த்தி சீராக உள்ளதால்

இங்கும் g' < g.

ஆழம் அதிகரிக்கும் போது g’ மதிப்பு குறைகிறது. எனவே புவியின் மேற்பரப்பில் ஈர்ப்பின் முடுக்கம் பெருமமாக இருக்கிறது. ஆனால் பரப்புக்கு உயரே சென்றாலோ அல்லது புவியின் ஆழத்திற்கு சென்றாலோ ஈர்ப்பின் முடுக்கம் குறையும்.

குறுக்குக்கோட்டைப் ( latitude) பொருத்து g மாறுதல் 

சுழலும் குறிப்பாயத்தில் இயங்கும் பொருள்களின் இயக்கத்தை நாம் பகுத்தாயும் போது (அலகு 3 இல் விளக்கப்பட்டுள்ளது) மையவிலக்கு விசையையும் நாம் கருத்தில் கொள்ள வேண்டும். பொதுவாக பூமியினை நிலைமக்குறிப்பாயமாக கருதுவோம். ஆனால் உண்மைலேயே பூமி ஒரு சுழலும் குறிப்பாயம். ஏனெனில் பூமியானது தனது அச்சைப்பற்றி சுழல்கிறது. எனவே புவிப்பரப்பில் ஒரு பொருள் உள்ளபோது, அது மைய விலக்கு விசையினை உணருகிறது. அவ்விசையானது புவியின் குறுக்குக் கோட்டு மதிப்பை சார்ந்துள்ளது. புவி சுழலவில்லை எனில் பொருளின் மீதான விசை mg ஆகும். ஆனால் புவி சுழற்சியின் காரணமாக பொருள் கூடுதலாக மைய விலக்கு விசையினை உணர்கிறது.

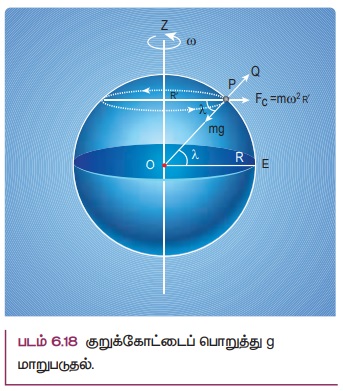
மையவிலக்கு விசை = mω2R’.

இங்கு λ என்பது குறுக்கு கோட்டின் மதிப்பு

பொருளின் மீது g க்கு எதிர்திசையில் செயல்படும் மையவிலக்கு முடுக்கத்தின் கூறு

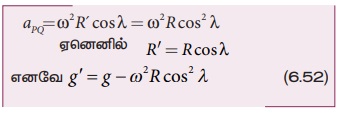
புவிமையக்கோட்டில் λ = 0;  எனவே சமன்பாடு (6.52) ஆனது பின்வருமாறு மாறுகிறது g’= g - ω2R. புவிமையக்கோட்டில் ஈர்ப்பின் முடுக்கம் g ஆனது சிறுமம் ஆகும். 

துருவப்பகுதியில் λ= 90° எனவே; g’ = g, 

ஆகவே துருவப் பகுதியில் ஈர்ப்பின் முடுக்கம் பெருமம் ஆகும்.

எடுத்துக்காட்டு 6.8

உன் பள்ளி ஆய்வகத்தில் g' மதிப்பினைக் காண்க.

தீர்வு 

உன் பள்ளி அமைந்துள்ள ஊர்/ நகரத்தின் குறுக்குக் கோட்டு மதிப்பினை கணினியில் கூகுள் தேடுதல் மூலம் காண்க.

உதாரணமாக சென்னைக்கு குறுக்குக் கோட்டு மதிப்பு 13° ஆகும்.

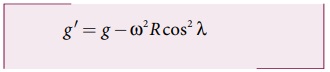
இங்கு  ω2R = (2x3.14/86400)2 × (6400x103) = 3.4 ×10−2 m s−2.

λ ன் மதிப்பு ரேடியனில் இருக்க வேண்டும். டிகிரியில் இருக்கக் கூடாது. 13° என்பது 0.2268 ரேடியனுக்குச் சமம்.

g′ = 9.8 − ( 3.4 × 10−2 ) × ( cos 0.2268)2

g′ = 9.7677 m s−2

சிந்தனைக்கு 

கிழக்கிலிருந்து மேற்கு நோக்கி குறுக்கு கோட்டின் திசையில் செல்கிறாய் எனில் g ன் மதிப்பு மாறுபடுமா?