புவியின் பரப்புக்கு அருகே ஈர்ப்புநிலை ஆற்றல்

புவியின் பரப்புக்கு அருகே ஈர்ப்புநிலை ஆற்றல்

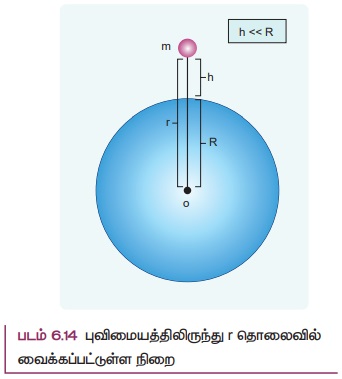
புவியிலிருந்து h உயரத்திற்கு கொண்டு செல்லப்பட்ட நிறை m இல் நிலை ஆற்றல் 'mgh' (படம் 6.14) சேமிக்கப்பட்டுள்ளது என்பதை அலகு 4 இல் ஏற்கனவே விவாதித்துள்ளோம்.

இச்சமன்பாட்டை, ஈர்ப்பு நிலை ஆற்றல் வழியேயும் தருவிக்கலாம்.

புவிமையத்திலிருந்து r தொலைவில் உள்ள நிறை m மற்றும் புவியையும் சேர்த்து ஒரு அமைப்பாகக் கருதுவோம். 

இந்த அமைப்பின் ஈர்ப்பு நிலை ஆற்றல்

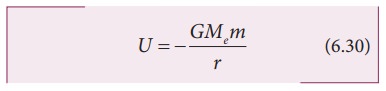
இங்கு r = Re + h மேலும் Re புவியின் ஆரம் ஆகும்.

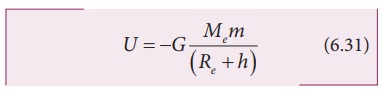
சமன்பாடு (6.31) ஐ நாம் கீழ்க்கண்டவாறு மாற்றி அமைக்கலாம்.

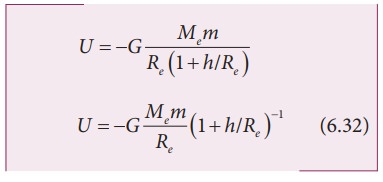
இங்கு h << Re. எனவே 

ஈருறுப்பு தேற்றத்தை (Binomial theorem) பயன்படுத்தி விரிவுபடுத்தி பின்பு உயர் அடுக்கு உறுப்புகளை புறக்கணித்தால், நாம் பெறுவது

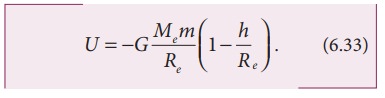
புவியின் பரப்பில் நிறை m உள்ள போது,

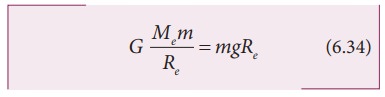
.என்பது நாம் அறிந்ததே. 

சமன்பாடு 6.34 ஐ 6.33 இல் பிரதியிட

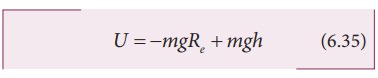
மேற்கண்ட சமன்பாட்டில் முதல் கோவை (first term) உயரம் h ஐ சார்ந்தது அல்ல. உதாரணமாக, h1 உயரத்தில் இருந்து h2, உயரத்திற்கு பொருள் எடுத்துச் செல்லப்படுகிறது என்க. 

h1 உயரத்தில் ஈர்ப்பு நிலை ஆற்றல்

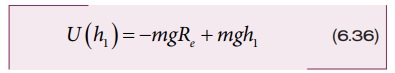
h2 உயரத்தில் ஈர்ப்பு நிலை ஆற்றல்

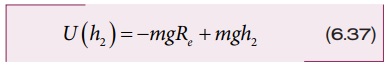
h1, மற்றும் h2 இடையே ஈர்ப்பு நிலை ஆற்றல் வேறுபாடு

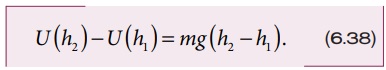
சமன்பாடு 6.36 மற்றும் 6.37-ல் உள்ள mgRe கோவை, ஈர்ப்பு நிலை ஆற்றல் மாறுபாடு காண்பதில் எவ்வித மாற்றத்தையும் ஏற்படுத்தவில்லை. எனவே சமன்பாடு 6.35 ல் முதல் கோவையை புறக்கணிக்கலாம். அல்லது சுழி என எடுத்துக் கொள்ளலாம். ஆகவே புவி பரப்பிலிருந்து h உயரத்தில் உள்ள நிறை m இல் சேமிக்கப்பட்டுள்ள ஈர்ப்பு நிலை ஆற்றல் U = mgh என கூறலாம்.

புவிப்பரப்பில் h = 0, என்பதால் U = 0

இங்கு நாம் கவனிக்க வேண்டியது நிறை 'm' ஐ புவிபரப்பில் இருந்து நாம் 'h' உயரம் உயர்த்த செய்த வேலையே "mgh" ஆகும். இந்த வேலை நிறை m இல் ஈர்ப்பு நிலை ஆற்றலாக சேமிக்கப்பட்டுள்ளது. உண்மையில் 'mgh' என்பது நிறை ‘m' மற்றும் புவியை சேர்த்த ஈர்ப்பு நிலை ஆற்றல் ஆகும். ஆயினும் இந்த ‘mgh' ஐ நிறை ‘m’ இன் ஈர்ப்பு நிலை ஆற்றலாகவே எடுத்துக் கொள்கிறோம் ஏனெனில் நிறை 'm' உயரம் 'h' க்கு செல்லும்போது புவி நிலையாகவே உள்ளது.