11வது இயற்பியல் : அலகு 6 : ஈர்ப்பியல்
ஈர்ப்பு புலத்தின் மேற் பொருந்துதல் தத்துவம்
ஈர்ப்பு புலத்தின் மேற் பொருந்துதல் தத்துவம்
m1, m2,,..... mn நிறையுடைய 'n' துகள்களின் நிலை வெக்டர்கள் முறையே ![]() 1 ,
1 , ![]() 2 ,
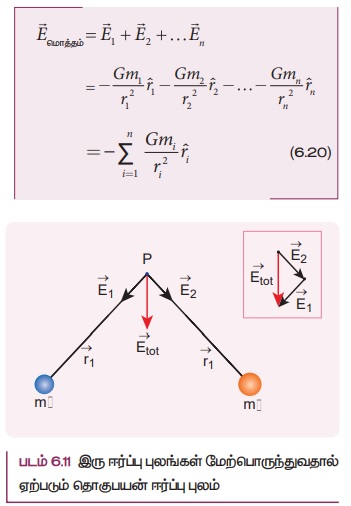
2 , ![]() 3 … என்க. புள்ளி P யில் தொகுபயன் ஈர்ப்புப்புலமானது தனித்தனி நிறைகளால் ஏற்படும் தனித்தனி ஈர்ப்புப் புலத்தின் வெக்டர் கூடுதலுக்கு சமம். (படம் 6.11) இத்தத்துவம் ஈர்ப்புபுலங்களின் மேற்பொருந்துதல் தத்துவம் எனப்படும்.
3 … என்க. புள்ளி P யில் தொகுபயன் ஈர்ப்புப்புலமானது தனித்தனி நிறைகளால் ஏற்படும் தனித்தனி ஈர்ப்புப் புலத்தின் வெக்டர் கூடுதலுக்கு சமம். (படம் 6.11) இத்தத்துவம் ஈர்ப்புபுலங்களின் மேற்பொருந்துதல் தத்துவம் எனப்படும்.
தனித்தனி நிறைகளுக்கு பதிலாக தொடர்ச்சியாக பரவியுள்ள மொத்த நிறை M - ஐ கருதினால் புள்ளி P யில் ஈர்ப்பு புலத்தை தொகையீட்டு முறையில் (integration method) கணக்கிடலாம்.
எடுத்துக்காட்டு 6.3
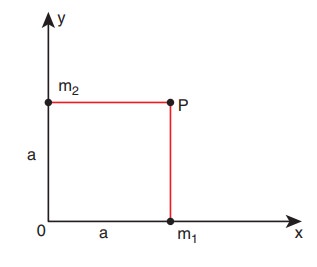
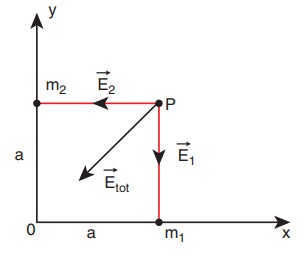
(a) நிறைகள் m1, மற்றும் m2 முறையே x மற்றும் y அச்சுகளில் ஆதியிலிருந்து ‘a’ தொலைவில் வைக்கப்பட்டுள்ளன. படத்தில் காட்டப்பட்டுள்ள புள்ளி P யில் ஈர்ப்பு புலச்செறிவு காண்க.
தீர்வு:
நிறை m1 ஆல் புள்ளி P யில் ஈர்ப்பு புலம்,
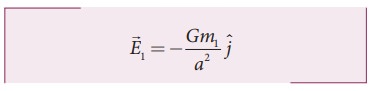
நிறை m2 ஆல் புள்ளி P யில் ஈர்ப்பு புலம்,
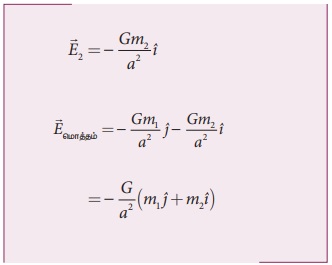
தொகுபயன் ஈர்ப்பு புலச்செறிவின் திசையானது m1 மற்றும் m2 ஒப்பீட்டு மதிப்பை பொறுத்து அமையும்.
m1 = m2 = m எனில்
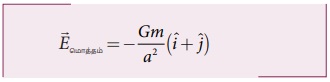
குறிப்பு: வெக்டர் கூட்டல் பரிமாற்று தன்மையுடையது
 இன் எண்மதிப்பு
இன் எண்மதிப்பு 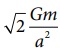 மேலும்
மேலும் 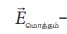 -இன் திசை ஆதிப்புள்ளி 0 வை நோக்கி அமைந்துள்ளது. இது அடுத்து உள்ள படத்தில் காட்டப்படுகிறது.
-இன் திசை ஆதிப்புள்ளி 0 வை நோக்கி அமைந்துள்ளது. இது அடுத்து உள்ள படத்தில் காட்டப்படுகிறது.
எடுத்துக்காட்டு 6.4
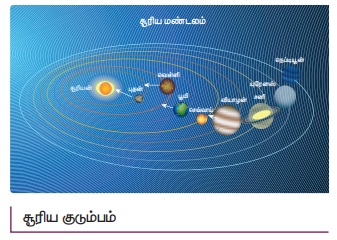
சூரிய குடும்பத்தின் படம் தரப்பட்டுள்ளது. இதிலிருந்து புதன், புவி மற்றும் வியாழன் கோள்கள் மீதான சூரியனின் ஈர்ப்பியல் புலங்களின் தன்மையினை குறிப்பிடுக.
தொலைவு அதிகரித்தால் ஈர்ப்பு புலம் குறையும். எனவே சூரியன் வியாழன் மீது ஏற்படுத்தும் ஈர்ப்பு புலம் குறைவாக இருக்கும். சூரியனுக்கு மிக அருகே உள்ள புதனின் மீது செயல்படும் ஈர்ப்பு புலம் அதிகமாக இருக்கும்.