பொது ஈர்ப்பியல் விதி

பொது ஈர்ப்பியல் விதி

கோள்களின் இயக்கம் பற்றி கெப்ளர் விதிகள் விளக்கி கூறிய போதும், அக்கோள்களின் இயக்கத்திற்கு காரணமான விசைகளை பற்றி விளக்க முடியவில்லை. கெப்ளர் விதிகளையும் கலிலியோவின் ஆய்வுகளை பகுப்பாய்வு செய்த நியூட்டன் அவற்றின் அடிப்படையில் ஈர்ப்பியல் விதியை தருவித்தார்.

M நிறை உடைய துகள், அண்டத்தில் உள்ள அனைத்து துகள்களையும் குறிப்பிட்ட விசையுடன் ஈர்க்கிறது. அந்த ஈர்ப்பு விசையின் வலிமையானது, அவற்றின் நிறைகளின் பெருக்கற்பலனுக்கு நேர்த்தகவிலும், அவற்றுக்கு இடையேயான தொலைவின் இருமடிக்கு எதிர்த்தகவிலும் இருக்கும் என்பதே நியூட்டனின் ஈர்ப்பியல் விதியாகும்.

கணிதவியல் வடிவில் ஈர்ப்பியல் விசையினை கீழ்கண்டவாறு எழுதலாம்.

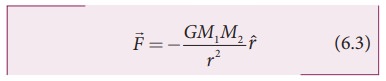
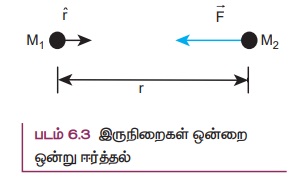
இங்கு M1 லிருந்து M2 நோக்கி செல்லும் அலகு வெக்டர் / ஆகும். (படம் 6.3 பார்க்க) G ஈர்ப்பியல் மாறிலி; G ன் மதிப்பு 6.626 × 10−11 N m2 kg−2 . r-என்பது நிறைகள் M1 மற்றும் M2 இடையே உள்ள தொலைவு. நிறை M1 ஆனது நிறை M2 ஆல் உணரும் ஈர்ப்பியல் விசையை படம் 6.3 ல் வெக்டர் குறிக்கிறது. எதிர்க்குறியானது ஈர்ப்பியல் விசை எப்பொழுதும் ஈர்க்கும் தன்மை உடையது என்பதை குறிக்கிறது. ஈர்ப்பியல் விசையானது எப்போதும் இரு நிறைகளையும் இணைக்கும் நேர்க்கோட்டின் வழியே செயல்படும்.

கார்டீசியன் ஆய அச்சுகளில் 'r' என்ற தொலைவின் இருமடி r 2 = (x2 + 2 z2) என குறிக்கப்படும் (பார்க்க : அலகு 2)

எடுத்துக்காட்டு 6.1 

படத்தில் காட்டியுள்ளபடி, 10 மீ தொலைவில் நிறைகள் m1 மற்றும் m2 அமைந்துள்ளன. இரு நிறைகளுக்கும் இடையேயான ஈர்ப்பியல் விசையை கணக்கிடுக. ஒவ்வொரு நிறையின் மீது செயல்படும் விசையின் திசையினை வரைக. (m1= 1 kg; m2 = 2 kg)

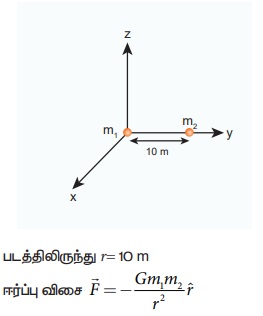
ஃ விசையின் எண் மதிப்பு 

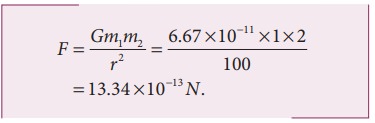
இவ்விசையின் எண் மதிப்பு மிகக்குறைவாக உள்ளது என்பது கவனிக்கத்தக்கது. இதனால் தான் இரு மனிதர்களுக்கிடையேயான ஈர்ப்பியல் விசையை நாம் உணர முடிவது இல்லை. ஈர்ப்பியல் விசையின் வலிமையை நிர்ணயம் செய்வதில் G-ன் மிகக்குறைந்த மதிப்பு முக்கியப் பங்காற்றுகிறது.

நிறை m1 ஆல் நிறை m2 உணரும் ஈர்ப்பியல் விசை  () yஅச்சு எதிர்த்திசையில் செயல்படுகிறது. அதாவது rˆ =−jˆ

நியூட்டனின் மூன்றாம் விதிப்படி, நிறை m1 ஆனது நிறை m2 மீது நிறை சமமான எதிர்த்திசையில் செயல்படும் விசையை ஏற்படுத்துகிறது. எனவே நிறை m2 ஆல் m1 உணரும் ஈர்ப்பியல் விசை () ஆனது y அச்சின் நேர்திசையில் செயல்படுகிறது. ie., rˆ = jˆ

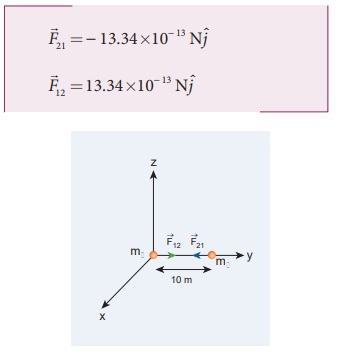
படத்தில் விசைகள் செயல்படும் திசை குறிக்கப்பட்டுள்ளன. மேலும் = − என்பது, நியூட்டனின் மூன்றாம் விதியை உறுதிப்படுத்துகிறது.

ஈர்ப்பியல் விசையின் முக்கிய பண்புகள்

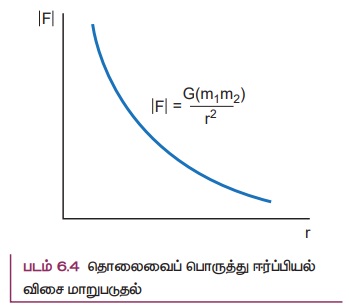
• ஈர்ப்பியல் விசையானது r2 க்கு எதிர்த் தகவில் உள்ளதால் இரு நிறைகளுக்கு இடையேயான தொலைவு அதிகரிக்கும் போது, ஈர்ப்பியல் விசையின் வலிமை குறைகிறது. ஆகவேதான் சூரியனிடமிருந்து புவியை விட அதிக தொலைவில் உள்ள யுரேனஸ் புவியினை விட குறைந்த அளவு ஈர்ப்பியல் விசையினை உணர்கிறது.

• இரு துகள்களுக்கு இடையே செயல்படும் ஈர்ப்பியல் விசை எப்பொழுதும் செயல் எதிர்ச்செயல் (action -reaction) இணையாகவே அமையும். புவி மீது சூரியன் ஏற்படுத்தும் ஈர்ப்பியல் விசை சூரியனை நோக்கி செயல்படும். அதேபோல் சூரியன் மீது புவி ஏற்படுத்தும் ஈர்ப்பியல் விசை புவியை நோக்கி செயல்படும். இது எதிர்ச்செயல் விசை (reaction force) ஆகும். இரு விசைகளும் வெவ்வேறு பொருள்களின் மீது செயல்படுகின்றன. 

• சூரியனின் ஈர்ப்பு விசையினால் பூமியின் மீது ஏற்படும் திருப்பு விசையானது கீழே தரப்பட்டுள்ளது

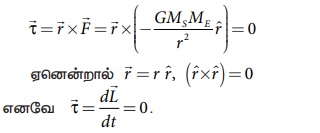
இதிலிருந்து அறிவது என்னவென்றால் பூமியின் கோண உந்தம் சூரியனைப் பொறுத்து ஒரு மாறா வெக்டராகும் இது அனைத்துக் கோள்களுக்கும் பொருந்தும். இன்னும் சொல்வதென்றால் இந்த கோண உந்த மாறாத் தன்மைதான் கெப்ளரின் இரண்டாம் விதியை ஏற்படுத்துகிறது.

• M1 மற்றும் M2 நிறைகள் புள்ளி நிறைகள் என்ற அனுமானத்தின் அடிப்படையிலேயே 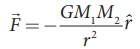சமன்பாடு பயன்படுத்தப்படுகிறது. சூரியனின் ஈர்ப்பு விசையின் காரணமாக புவியானது சூரியனைச் சுற்றி வருகிறது எனும்போது நாம் சூரியனையும் புவியையும் புள்ளி நிறைகளாக கருதுகிறோம். சூரியனுக்கும் புவிக்கும் இடையே உள்ள தொலைவினை அவற்றின் விட்டத்துடன் ஒப்பிடும் போது அவற்றை புள்ளி நிறைகளாக கருதுவதில் தவறில்லை. சமன்பாடு (6.3) ஐ ஒழுங்கற்ற மற்றும் நீட்டிக்கப்பட்டுள்ள பரப்புடைய (irregular and extended) பொருள்களுக்கு பயன்படுத்த இயலாது. அப்படிப்பட்ட பொருள்களுக்கு இடையே உள்ள ஈர்ப்பு விசையின் கணக்கீட்டு முறைகளை உயர் வகுப்புகளில் கற்போம்.

• ஒரே ஒரு சிறப்பு நேர்வில் மட்டும் இருபொருள்கள் மிக அருகில் இருந்தாலும், புள்ளிநிறை என்ற அனுமானத்தை பயன்படுத்தலாம்.

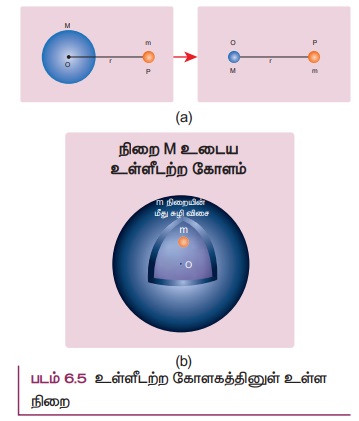
சீரான அடர்த்தியும் நிறை M மும் உடைய உள்ளீடற்ற கோளத்திற்கும், அக்கோளத்திற்கு வெளியே உள்ள புள்ளி நிறைறக்கும் இடையே உள்ள ஈர்ப்பியல் விசையை கணக்கிடும் போது, இவை இரண்டும் குறைந்த தொலைவில் உள்ள போதும் கோளத்தை புள்ளி நிறை என கருதி ஈர்ப்பியல் விசை சமன்பாட்டை பயன்படுத்தலாம். உள்ளீடற்ற கோளத்திற்கு பதிலாக நிறை M உடைய புள்ளி நிறையானது அக்கோளத்தின் மையப்புள்ளியில் உள்ளதாகக் கருதுவோம். பின்பு இவ்விரு புள்ளி நிறைகளுக்கும் இடையே உள்ள ஈர்ப்பியல் விசையை கணக்கிடலாம். இந்த மதிப்பு உள்ளீடற்ற கோளத்திற்கும் புள்ளி நிறைக்கும் இடையேயான ஈர்ப்பியல் விசைக்கு சமம் ஆகும். உள்ளீடற்ற கோளத்தின் மொத்த நிறையும் அதன் மையப்புள்ளியில் இருப்பது போல தோன்றும். இது படம் 6.5 (a)ல் காட்டப்பட்டுள்ளது

• நம்மை கவரக்கூடிய மற்றொரு முடிவும் உள்ளது. நிறை M உடைய உள்ளீடற்ற கோளம் ஒன்றை கருதுவோம். உள்ளீடற்ற கோளத்தின் உட்புறம் நிறை m ஐ வைப்போம். (படம் 6.5 (5)) நிறை m உணரும் ஈர்ப்பியல் விசை சுழி ஆகும். இதற்கான விளக்கத்தை உயர் வகுப்புகளில் கற்போம்.

• நன்கு பழுத்த மாங்கனி, மரத்திலிருந்து கீழே விழுவதற்கும், நிலா புவியை சுற்றுவதற்கும் காரணம் ஒரே ஈர்ப்பியில் விசைதான் என்று விளக்கியதே ஈர்ப்பியல் விதியின் வெற்றியாகும்.

நியூட்டனின் எதிர்த்தகவு இருமடி விதி 

நியூட்டன் ஒரு எளிமையான கணக்கீட்டுக்காக கோள்கள் வட்டப்பாதையில் இயங்குவதாக கருதினார். r ஆரமுடைய வட்டப்பாதையில் இயங்கினால் மையப்புள்ளியை நோக்கி செயல்படும் மைய நோக்கு முடுக்கம்

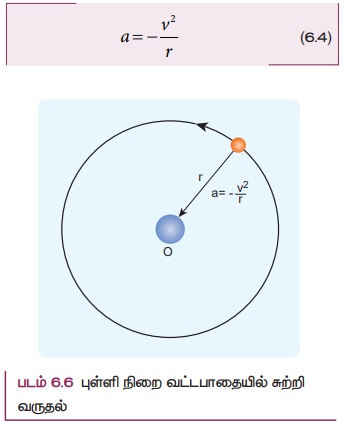
இங்கு v - திசைவேகம் மற்றும் r - வட்டப்பாதையின் மையப்புள்ளியிலிருந்து கோளின் தூரம் ஆகும். (படம் 6.6)

தெரிந்த அளவுகள் r மற்றும் T ஆகியவற்றின் அடிப்படையில் திசைவேகம்

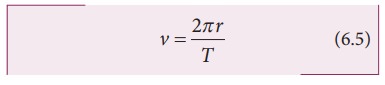
இங்கு T என்பது கோளின் சுற்றுக்காலம் ஆகும். என் மதிப்பை சமன்பாடு 6.4 இல் பிரதியிட

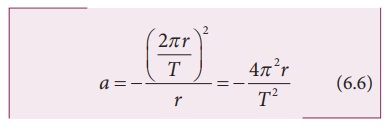
இந்த a- ன் மதிப்பை நியூட்டன் இரண்டாம் விதி F=ma சமன்பாட்டில் பிரதியிட

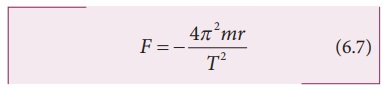
இங்கு m என்பது கோளின் நிறை ஆகும். கெப்ளர் மூன்றாம் விதிப்படி

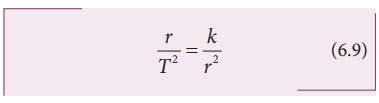
சமன்பாடு 6.9 ஐ விசைக்கான சமன்பாடு (6.7)ல் பிரதியிட நமக்கு ஈர்ப்பியல் விதிக்கான சமன்பாடு கிட்டும்

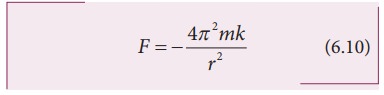
இவ்விசையானது கவர்ச்சி விசை என்பதையும் விசையானது மையத்தை நோக்கி செயல்படும் என்பதையும் எதிர்க்குறி உணர்த்துகிறது. சமன்பாடு (6.10)ல் கோளின் நிறை m ஆனது வெளிப்படையாக வந்துள்ளது. ஆனால் நியூட்டன் தனது மூன்றாம் விதிப்படி புவியானது சூரியனால் ஈர்க்கப்படுகிறது எனில் சூரியனும் புவியால் ஈர்க்கப்பட்ட வேண்டும் என உறுதியாக நம்பினார். எனவே 6.10 சமன்பாட்டில் சூரியனின் நிறை M மும் வெளிப்படையாக இடம்பெற வேண்டும் என நியூட்டன் கருதினார். ஆகவே தன் உள் உணர்வின்படி 4π2k க்கு பதிலாக GM என சமன்பாட்டில் பிரதியிட்டார். அதன்மூலம் ஈர்ப்பியல் விதி சமன்பாடு

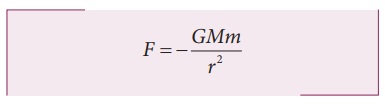
எனப் பெறப்பட்டது.

ஈர்ப்பியல் விசையானது கவர்ச்சி என்பதை எதிர்க்குறி மீண்டும் நமக்கு உணர்த்துகின்றது. மேற்கூறிய விவாதத்தில், கோள் வட்டப்பாதையில் இயங்குகிறது என நாம் எடுத்து கொண்டோம். ஆனால் கோள்கள் சூரியனை நீள்வட்டப்பாதையில் சுற்றி வருகின்றன என்பதே உண்மையாகும். ஆயினும் கோள்களின் பாதையானது, வட்டப்பாதையிலிருந்து சிறிதளவே மாறுபட்டு உள்ளன. மேலும் பெரும்பாலான கோள்களின் பாதை கிட்டத்தட்ட வட்டமாகவே உள்ளது என்பதால் மேற்கண்ட கருதுகோள் சரியே.

உங்கள் சிந்தனைக்கு

“r3/T2 = மாறிலி" பதிலாக "r3/T2 = மாறிலி" என கெப்ளரின் மூன்றாம் விதி அமைந்தால், பொது ஈர்ப்பியல் விதி எவ்வாறு அமையும்? இருமடி எதிர்த்தகவு விதியாகவே அமையுமா? இப்புதிய ஈர்ப்பியல் விதியின் அடிப்படையில் நெப்டியூன் உணரும் ஈர்ப்பியல் விசை, புவி உணரும் விசையை விட அதிகமாக இருக்குமா? அல்லது குறைவாக இருக்குமா?

எடுத்துக்காட்டு 6.2

நிலவும் ஆப்பிளும் ஒரே ஈர்ப்பியல் விசையாலேயே முடுக்கமடைகிறது. இவை இரண்டும் அடையும் முடுக்கங்களை ஒப்பிடுக.

புவியினால் ஆப்பிள் உணரும் ஈர்ப்பியல் விசை

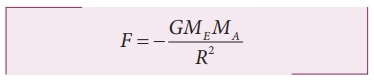
இங்கு MA- ஆப்பிள் நிறை, ME புவியின் நிறை, R - புவியின் ஆரம் ஆகும்.

நியூட்டன் இரண்டாம் விதியைப் பயன்படுத்த

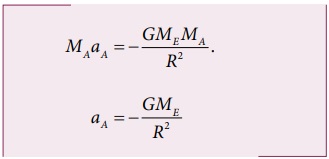
இங்கு ‘aA' ஆப்பிளின் முடுக்கம். இது 'g' க்கு சமம்

இதேபோல் புவியினால் நிலா உணரும் விசை

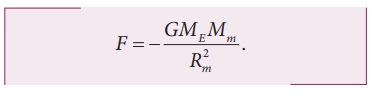
இங்கு Rm - புவிக்கும் நிலாவுக்கும் உள்ள தொலைவு, Mm - நிலாவின் நிறை

நிலா உணரும் முடுக்கம்

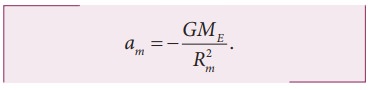
ஆப்பிளின் முடுக்கத்திற்கும், நிலாவின் முடுக்கத்திற்கும் இடையே உள்ள தகவு

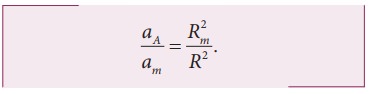
நிலாவின் சுற்றுப்பாதையானது புவியின் ஆரத்தை போல 60 மடங்கு என ஹிப்பார்க்கஸ் (Hipparchus) முன்னரே கண்டறிந்துள்ளார்.

Rm = 60R.

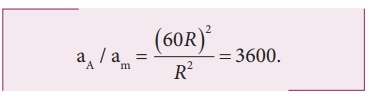
இதன் மூலம் ஆப்பிளின் முடுக்கமானது, நிலாவின் முடுக்கத்தைப் போல 3600 மடங்கு பெரியது என அறிகின்றோம். தனது ஈர்ப்பியல் சமன்பாட்டின் மூலம் இதே முடிவை நியூட்டன் பெற்றார். ஆப்பிளின் முடுக்கம் 9.8ms-2 என எளிதில் கண்டறியப்பட்டது. புவியினை சுற்றும் நிலாவின் சுழற்சிகாலம் 27.3 நாட்கள் என்பதை மைய நோக்கு முடுக்கச் சமன்பாட்டில் பயன்படுத்த, நமக்கு கிடைப்பது

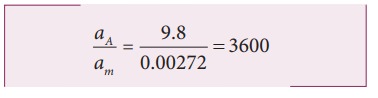
ஈர்ப்பியல் விதியின் மூலமாகவும் இதே மதிப்பினையே நியூட்டன் பெற்றார்.

குறிப்பு

புவிக்கும் நிலவுக்கும் இடையே உள்ள தொலைவு மற்றும் புவியின் ஆரம் ஆகியவற்றின் மதிப்புகளின் மூலம் மேற்கண்ட கணக்கீடு அமைந்துள்ளது.

2400 ஆண்டுகளுக்கு முன்னர் கிரேக்க நூலகர் (எரட்டோஸ்த னீஸ்) (ERATOSTHENIS) புவியின் ஆரத்தை கணக்கிட்டார். அதேபோல கிரேக்க வானியல் அறிஞர் ஹிப்பார்க்கஸ் புவிக்கும் நிலவுக்கும் இடையே உள்ள தொலைவைக் கண்டறிந்தார். சுவாரசியமான விஷயம் என்னவென்றால் இத்தொலைவுகளைக் கணக்கிட இவ்வானவியல் அறிஞர்கள் பயன்படுத்திய வடிவியல் மற்றும் முக்கோணவியல் இன்று நாம் உயர்நிலை பள்ளி வகுப்புகளிலேயே கற்கிறோம். வானியல் பகுதியில் இது பற்றிய விவபரங்கள் தரப்பட்டுள்ளன.